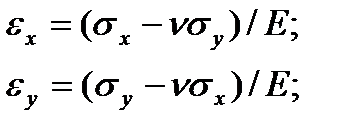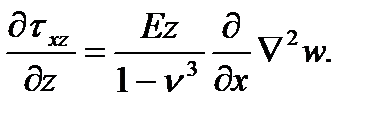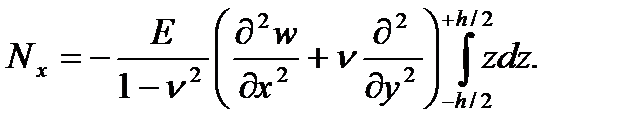Напряжения в пластинке
Чтобы вычислить нормальные напряжения σx и σy воспользуемся двумя формулами закона Гука
(1.7)
и на основании третьей гипотезы отбросим напряжение σz. Получим:
Отсюда, учитывая зависимости (1.6) найдем
(а)
Четвертая формула закона Гука после подстановки угловой деформации γxy из формул (1.6) принимает вид:
(б)
В двух других плоскостях касательные напряжения, согласно равенствам (1.1), обращаются в нуль:
Однако такой результат получен только вследствие принятых ранее гипотез. В действительности эти касательные напряжения не равны нулю, поскольку это противоречит условиям равновесия. Рассмотрим дифференциальные уравнения равновесия
(1.8)
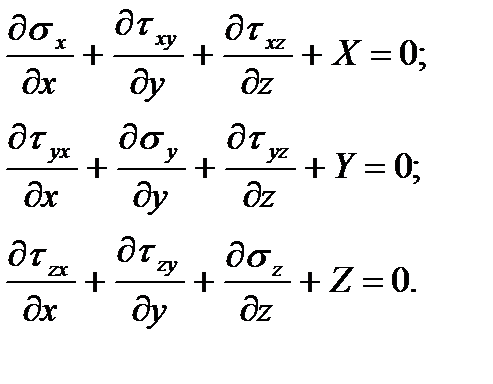
Пренебрегая объемными силами, из первого уравнения найдем
Подставив сюда напряжения из формул (а) и (б) получим:
Проинтегрировав по z, найдем
(в)
Для определения произвольной функции f 3(x,y) имеем следующие граничные условия: на верхней и нижней поверхностях пластинки нет касательных нагрузок, т. е. при z =±h/2 τzx=0. Подставив эти условия в формулу (в), получим
Вводя ее в формулу (в), получаем
(г)
Решив таким же путем второе уравнение равновесия (1.8), находим
(д)
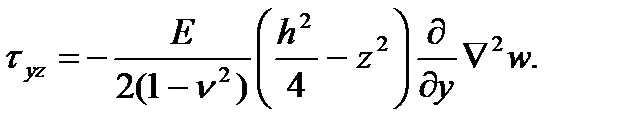
Согласно формулам (а), (б), (г) и (д), в сечениях пластинки, перпендикулярных ее срединной плоскости, возникают следующие напряжения:
(1.9)
На рис. 1.2 показаны эпюры этих напряжений по толщине пластинки. Напряжения σx, σy и τxy = τyx распределяются по линейному закону, обращаясь в нуль в точках срединной плоскости; напряжения τzy и τzx распределяются по параболе, достигая в точках срединной плоскости максимального значения. Так же распределяются касательные напряжения и при поперечном изгибе балок прямоугольного сечения. В формулах (1.9) все напряжения выражены через одну функцию двух переменных w (x, y), следовательно, функция прогибов играет здесь ту же роль, что и функция напряжений в плоской задаче.
Усилия в пластинке.
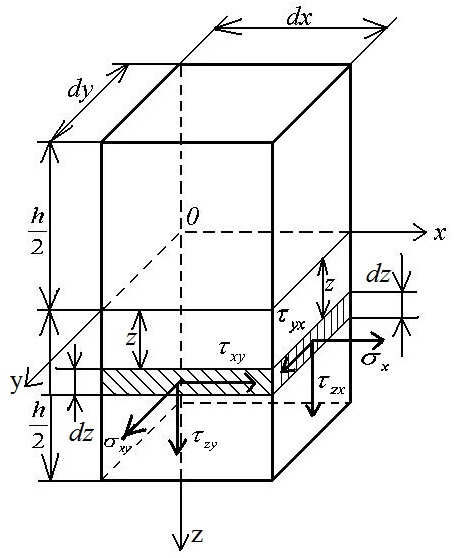
Найдем усилия, соответствующие напряжениям (1.9) в сечениях пластинки, нормальных к ее срединной плоскости. На рис. 1.3 изображен бесконечно малый элемент пластинки.
На рисунке показаны положительные напряжения: нормальное напряжение σx направлено по внешней нормали к сечению, касательные – в направлении соответствующих положительных координатных осей.
Через Nx обозначим нормальную силу, приходящуюся на единицу ширины рассматриваемого сечения. Она равна проекции на ось x равнодействующей внутренних сил в сечении с нормалью, параллельной оси x. На ось x проецируется только нормальное напряжение σx. Соответствующая ему внутренняя сила на бесконечно малой площадке dydz равна σx dydz, а на единицу ширины сечения приходится сила σx dz. Суммируя эти элементарные силы по толщине пластинки, получим выражение нормальной силы
Подставим сюда нормальное напряжение σx из формул (1.9) и вынесем за знак интеграла величины, которые не зависят от координаты z:
Под знаком интеграла стоит нечетная функция, а пределы интегрирования отличаются только знаком. Поэтому интеграл равен нулю, а нормальная сила Nx = 0.
Аналогичным способом определяется изгибающий момент Mx, представляющий собой сумму элементарных моментов 
После интегрирования получим
(1.10)
называется цилиндрической жесткостью.
Поперечная сила в рассматриваемом сечении
Подставив в этот интеграл выражение касательного напряжения tzx из формул (1.9) получим
Сдвигающую силу Sx находим, суммируя проекции внутренних сил в том же сечении на ось y:
После подстановки tyx из формул (1.9)
(а)
Таким же способом определяются усилия в сечении с нормалью, параллельной оси y (Рис. 1.3):
(б)
Сравнив формулы (а)и (б), заметим, что
Отсюда следует, что под действием поперечной нагрузки в сечениях пластинки, перпендикулярных ее срединной плоскости, возникают следующие усилия:
изгибающие моменты
(1.11)
(1.12)
(1.13)
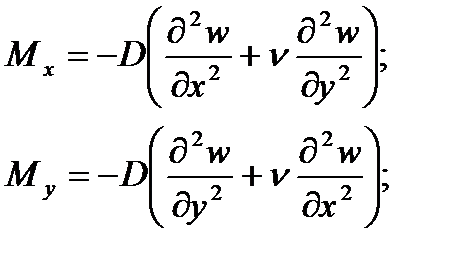
Все они выражены через прогибы срединной плоскости. Положительные направления указанных усилий показаны на рис. 1.4.
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Изгиб прямоугольных пластинок. Дифференциальное уравнение изогнутой поверхности пластинки
Для расчета тонких пластинок с 
прямоугольной и трапециевидной формы более удобными оказываются декартовы координаты 
Результатом использования гипотез Кирхгоффа в задаче изгиба пластинок в декартовой системе координат является:
— дифференциальное уравнение изогнутой поверхности:
, где: w = w (x,у) — функция прогиба, а 
— цилиндрическая жесткость.
Уравнение это называют уравнением Софи Жермен, оно представляет собою дифференциальное уравнение в частных производных четвертого порядка относительно функции w, зависящей от двух переменных (х и у). Общего решения этого уравнения, как и большинства других уравнений в частных производных, в математике неизвестно. Поэтому прямой метод решения, как это делается при решении обыкновенных дифференциальных уравнений, здесь оказывается невозможным, и приходится применять либо обратный метод (т. н. метод проб и ошибок) либо полуобратный метод, требующий всего одной попытки.
Наиболее универсальными, хотя и приближенными аналитическими методами расчета пластинок являются вариационные методы. Это метод Ритца-Тимошенко, метод Бубнова- Галеркина и метод Власова-Канторовича. Любой из них позволяет найти функцию прогиба w (x,у), удовлетворяющую как уравнению (1), так и конкретным граничным условиям на контуре пластинки. Все остальные параметры, в частности, усилия, напряжения, деформации и перемещения, определяются уже через найденную функцию прогиба. Приведем без вывода формулы внутренних усилий и напряжений в пластинке.
Усилия и напряжения в пластинках (пластинах). Внутренние усилия в сечениях пластинки:
— изгибающие моменты
— крутящие моменты 
— поперечные силы 
Соответственно шести усилиям в сечениях пластинки возникают и шесть составляющих напряжений:
— нормальные напряжения
— касательные напряжения, действующие параллельно срединной плоскости (с.п.) пластинки
— касательные напряжения, направленные перпендикулярно срединной плоскости пластинки
В формулах напряжений обозначено:
— момент инерции сечения шириной, равной 1 и высотой h (погонный момент инерции), z — расстояние от срединной плоскости пластинки до той точки, где определяется напряжение.
Покажем эпюры напряжений
Эпюры напряжений в прямоугольной пластинке при изгибе
Наибольших значений нормальные напряжения достигают в точках, расположенных у поверхностей пластинки, наиболее удаленных от срединной плоскости, при 
:
, где
— погонный метр сопротивления, то есть момент сопротивления сечения единичной ширины.
Касательные напряжения, параллельные срединной плоскости, достигают наибольшей величины тоже в точках у поверхностей пластинки:
а касательные напряжения, направленные перпендикулярно срединной плоскости, наоборот, имеют максимум в точках срединной плоскости (при z=0):
Для сравнения — в балке при изгибе возникают всего две составляющие напряжений: это σх и τzx.
Источник