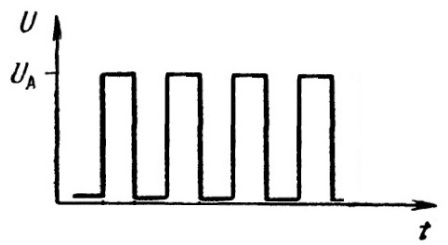
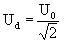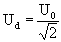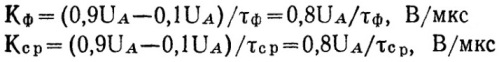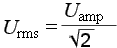Действующее значение напряжения для прямоугольных импульсов

Расчет действующего значения выходного напряжения
преобразователя в зависимости от формы сигнала

При использовании ветрогенераторов в качестве источника энергии необходимо иметь промежуточный накопитель энергии. Как правило, для этого используется аккумуляторная батарея с довольно низким выходным постоянным напряжением – 12 или 24 В . В то же время большинство потребительских нагрузок рассчитаны на подключение к сетям переменного тока напряжением 110 – 380 В частотой 45 – 65 Гц . Поэтому требуется преобразователь постоянного напряжения аккумуляторной батареи ( наиболее распространены автомобильные аккумуляторы напряжением 12 В) в переменное напряжение ( чаще всего 220 В 50 Гц) [1, 2].

Нагрузки, подключаемые в сеть переменного тока, могут не иметь блока питания и иметь индуктивный характер (вибрационный насос, электромагнит, электродвигатель ) или резистивный характер (лампа накаливания, нагревательный прибор ).

При наличии блока питания он может быть трансформаторным или бестрансформаторного типа.

Синусоидальная форма выходного сигнала преобразователя при малом коэффициенте гармоник соответствует паспортным требованиям нагрузок, подключаемых в сеть переменного тока , в частности, по соотношению амплитудного и действующего значений напряжения . Однако преобразователь с синусоидальной формой выходного сигнала сложен в конструировании и изготовлении. Желательно упростить преобразователь за счет использования других форм выходного сигнала, поняв условия, при которых такой преобразователь может использоваться для возможно большего количества типов нагрузок.

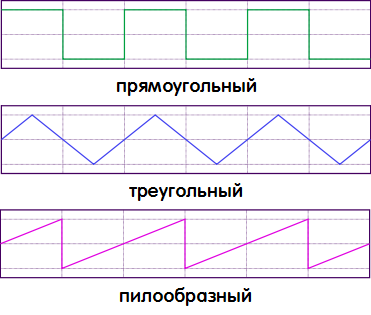
Форма выходного сигнала наиболее просто реализуемых преобразователей может быть прямоугольной, прямоугольной с паузой, трапецеидальной .

При этом возникает проблема выбора параметров сигнала, в частности, амплитудного значения напряжения. Для нагрузок с бестрансформаторным блоком питания , построенном по схеме выпрямитель-фильтр-преобразователь, максимальное амплитудное значение любого сигнала независимо от его формы может составлять 310 В, причем, как правило, это значение может быть существенно уменьшено .

Для нагрузок резистивного типа (ламп накаливания), рассчитанных на синусоидальное напряжение с действующим значением 220 В, амплитудное напряжение 310 В для сигнала прямоугольной формы без паузы является чрезмерным ( действующее значение сигнала прямоугольной формы равно его амплитудному значению, в данном случае 310 В), и его необходимо уменьшить .

Рассмотрим случай трансформаторного блока питания . Полоса пропускания трансформаторов по частоте весьма широкая (до тысяч герц), поэтому напряжение на выходе трансформатора будет иметь прямоугольную форму. Так как стоящие дальше по схеме стабилизаторы рассчитаны на использование переменного напряжения с амплитудным значением (приведенным ко входу) 310 В, то применение прямоугольного напряжения с амплитудным значением 310 В будет перегружать трансформатор, а при меньших значениях амплитуды ухудшатся условия работы стабилизаторов.

Величину действующего напряжения для периодического сигнала U_d = U(t) с периодом T и круговой частотой w = 2 p /T можно рассчитать по формуле:

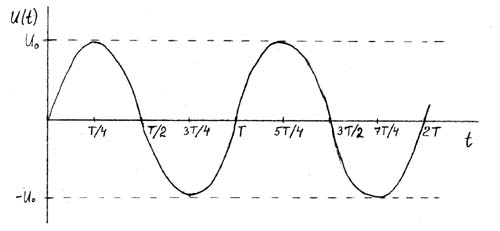
Для синусоидального сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U₀:

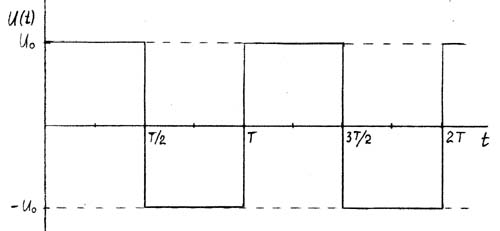
Для прямоугольного сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U₀:

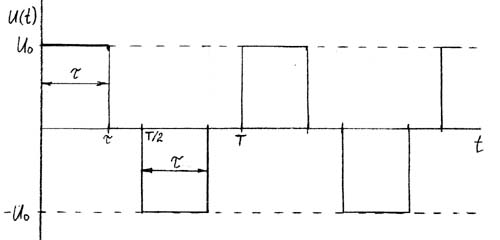
Для прямоугольного сигнала с паузой ( период T , круговая частота w = 2 p /T, длительность импульса положительной и отрицательной полярности t , длительность паузы T/2 – t ) с амплитудным значением U₀:

Для такого сигнала соотношение (2) достигается при t = T/4 , т. е. длительность импульса с положительной полярностью и длительность импульса с отрицательной полярностью t должна быть равна половине полупериода, а длительность паузы должна быть равна длительности импульса t . При этом действующее значение напряжения U_d будет равно действующему значению напряжения синусоидального сигнала с такой же амплитудой.

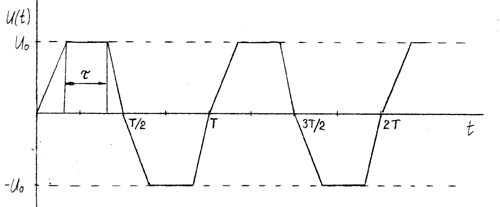
Для трапецеидального сигнала с периодом T, круговой частотой w = 2 p /T и амплитудным значением U₀:

Здесь t – длительность вершины импульса.

При t = T/8 ( четвертой части полупериода) действующее значение напряжения U_d будет таким же, как для случая синусоидального сигнала с такой же амплитудой U₀:

Принимая в качестве критерия соотношение для амплитудного и действующего значения выходного напряжения преобразователя как для случая синусоидального сигнала (2)

можно сделать вывод, что приемлемой формой выходного сигнала преобразователя является прямоугольная с паузой, когда длительность как отрицательного, так и положительного импульса равна длительности паузы (половина полупериода), или трапецеидальная, когда длительность плоской вершины импульса составляет четвертую часть полупериода . Выходной сигнал трапецеидальной формы предпочтительнее, так как коэффициент гармоник для него меньше.

Таким образом, возможно конструирование преобразователя с выходным сигналом трапецеидальной формы частотой 50 Гц, у которого длительность плоской вершины импульса составляет четвертую часть полупериода. Амплитуда выходного напряжения должна быть около 310 В. Действующее значение напряжения при этом будет равно 220 В. Такой преобразователь подходит по своим параметрам для большинства применяемых типов нагрузок.

• Амплитуда — максимальное абсолютное значение.
• Электрическое напряжение — разность электрических потенциалов в соответствующих точках.

11.12.2003
12.01.2006
17.04.2006
17.06.2010

Источник

Электрические и временные параметры прямоугольных импульсов

Периодические и непериодические сигналы, форма которых отличается от синусоидальной, обычно называют импульсными сигналами . Процессы генерации, преобразования, а также вопросы практического применения импульсных сигналов относятся сегодня ко многим областям электроники.

Так, например, ни один современный блок питания не обходится без расположенного на его печатной плате генератора прямоугольных импульсов, такого например как на микросхеме TL494, выдающей импульсные последовательности с параметрами, подходящими для текущей нагрузки.

Поскольку импульсные сигналы могут иметь различную форму, то и называют различные импульсы в соответствии с похожей по форме геометрической фигурой: прямоугольные импульсы, трапецеидальные импульсы, треугольные импульсы, пилообразные импульсы, ступенчатые, и импульсы разных других форм. Между тем, наиболее часто практически применяются именно прямоугольные импульсы . О их параметрах и пойдет речь в данной статье.

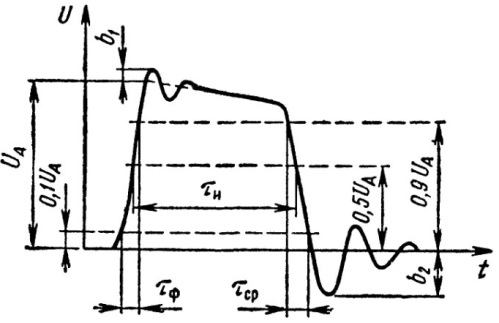
Конечно, термин «прямоугольный импульс» несколько условен. В силу того что ничего идеального в природе не бывает, как не бывает и идеально прямоугольных импульсов. На самом деле реальный импульс, который принято называть прямоугольным, может иметь и колебательные выбросы (на рисунке показаны как b1 и b2), обусловленные вполне реальными емкостными и индуктивными факторами.

Выбросы эти могут, конечно, отсутствовать, однако существуют электрические и временные параметры импульсов, отражающие в числе прочего «неидеальность их прямоугольности».

Прямоугольный импульс имеет определенную полярность и рабочий уровень. Чаще всего полярность импульса положительна, поскольку подавляющее большинство цифровых микросхем питаются положительным, относительно общего провода, напряжением, и следовательно мгновенное значение напряжения в импульсе всегда больше нуля.

Но есть, например, компараторы, питаемые двухполярным напряжением, в таких схемах можно встретить разнополярные импульсы. Вообще микросхемы, питаемые напряжением отрицательной полярности, не так широко применяются, как микросхемы с обычным положительным питанием.

В последовательности импульсов рабочее напряжение импульса может принимать низкий или высокий уровень, причем один уровень с течением времени сменяет другой. Уровень низкого напряжения обозначают U0, уровень высокого U1. Наибольшее мгновенное значение напряжения в импульсе Ua или Um, относительно начального уровня, называется амплитудой импульса .

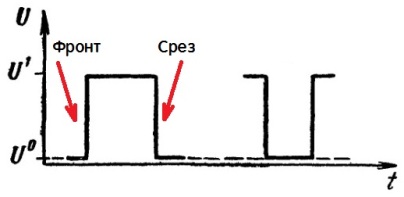
Разработчики импульсных устройств зачастую оперируют активными импульсами высокого уровня, такими как показанный на рисунке слева. Но иногда практически целесообразно применить в качестве активных импульсы низкого уровня, для которых исходное состояние — высокий уровень напряжения. Импульс низкого уровня показан на рисунке справа. Называть импульс низкого уровня «отрицательным импульсом» — безграмотно.

Перепад напряжения в прямоугольном импульсе называют фронтом, который представляет собой быстрое (соизмеримое по времени со временем протекания переходного процесса в цепи) изменение электрического состояния.

Перепад с низкого уровня к высокому уровню, то есть положительный перепад, называют передним фронтом или просто фронтом импульса. Перепад от высокого уровня к низкому, или отрицательный перепад, называют срезом, спадом или просто задним фронтом импульса.

Передний фронт обозначают в тексте 0.1 или схематически _|, а задний фронт 1.0 или схематически |_.

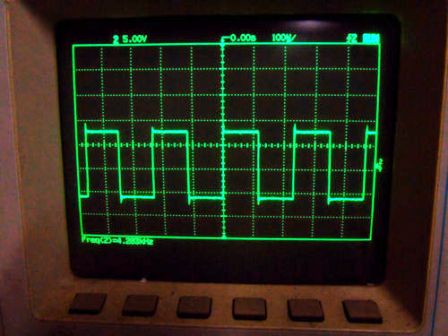
В зависимости от инерционных характеристик активных элементов, переходный процесс (перепад) в реальном устройстве всегда занимает некоторое конечное время. Поэтому полная длительность импульса включает в себя не только времена существования высокого и низкого уровней, но также времена длительности фронтов (фронта и среза), которые обозначаются Тф и Тср. Практически в любой конкретной схеме время фронта и спада можно увидеть при помощи осциллографа.

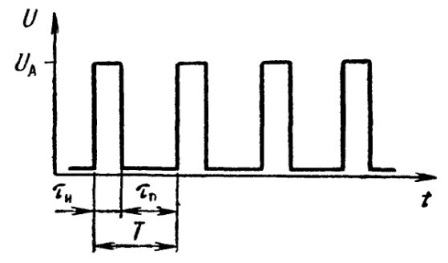
Так как в реальности моменты начала и окончания переходных процессов в перепадах очень точно выделить непросто, то принято считать за длительность перепада промежуток времени, во время которого напряжение изменяется от 0,1Ua до 0,9Ua (фронт) или от 0,9Ua до 0,1Ua (срез). Так и крутизна фронта Кф и крутизна среза Кс.р. задаются в соответствии с данными граничными состояниями, и измеряются в вольтах в микросекунду (в/мкс). Непосредственно длительностью импульса называют промежуток времени, отсчитываемый от уровня 0,5Ua.

Когда рассматривают в общем процессы формирования и генерации импульсов, то фронт и срез принимают по длительности за ноль, поскольку для грубых расчетов эти малые временные промежутки оказываются не критичны.

Импульсная последовательность — это импульсы, следующие друг за другом в определенном порядке. Если паузы между импульсами и длительности импульсов в последовательности равны между собой, то это периодическая последовательность. Период следования импульсов Т — это сумма длительности импульса и паузы между импульсами в последовательности. Частота f следования импульсов — это величина обратная периоду.

Периодические последовательности прямоугольных импульсов, кроме периода Т и частоты f, характеризуются еще парой дополнительных параметров: коэффициентом заполнения DC и скважностью Q. Коэффициент заполнения — это отношение времени длительности импульса к его периоду.

Скважность — это отношение периода импульса ко времени его длительности. Периодическая последовательность скважности Q=2, то есть такая, у которой время длительности импульса равно времени паузы между импульсами или у которой коэффициент заполнения равен DC=0,5, называется меандром.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Среднеквадратичное значение

В зарубежной терминологии применяется аббревиатура RMS (rms) — root mean square.
В математике для набора чисел x₁, x₂, . x_n количеством n среднеквадратичное значение (rms) определяется выражением:

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04

Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.

Для любой непрерывной функции в интервале T₁ — T₂ среднеквадратичное значение можно рассчитать по формуле:

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.

Действующее значение напряжения и тока

В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.

P = I²R; A = I²Rt; P = U²/R; A = U²t/R

Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P avg или работы A avg, пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.

Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.

Величину переменного напряжения или тока, в большинстве случаев, выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями — True RMS.

Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.

Расчёт действующего значения

В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение U rms с применением интеграла функции U = U ampsin(t) для одного периода 2π :

Вынесем U amp из под знака радикала. Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:

Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции , представленной на рисунке:

Выразим U rms искомой функции с помощью определённого интеграла:

Используя табличный интеграл и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F₁(t) , F₂(t) , . , F n(t) в соответствующих им интервалах времени (0 — T₁), (T₁ — T₂), . (T n — T), составляющих период T, действующее напряжение (RMS) определится выражением:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией , а интегралы, определённые в интервалах, равных T, для квадратов используемых функций , будут иметь одно и то же значение

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение .

В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью T i .

Выразим U rms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 — T i и T i — T для квадратов всех значений периода.

В результате получаем значение RMS, равное произведению амплитуды импульсов U amp на квадратный корень из коэффициента заполнения (T i / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.

Замечания и предложения принимаются и приветствуются!

Источник