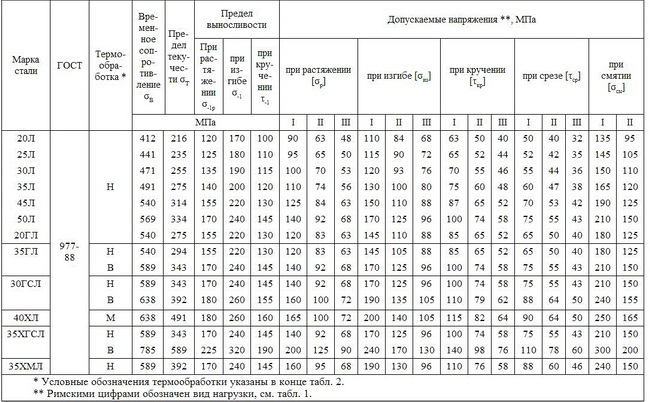
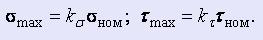- Допускаемые напряжения и механические свойства материалов
- Онлайн калькулятор по определению допускаемых напряжений материалов: сталей и сплавов алюминия, меди и титана.
- для углеродистых и низколегированных сталей
- для жаропрочных, жаростойких и коррозионно-стойких сталей аустенитного класса
- Нагрузки (виды нагрузок, единицы измерения нагрузок).
Допускаемые напряжения
и механические свойства материалов
Для определения допускаемых напряжений в машиностроении применяют следующие основные методы.
1. Дифференцированный запас прочности находят как произведение ряда частных коэффициентов, учитывающих надежность материала, степень ответственности детали, точность расчетных формул и действующие силы и другие факторы, определяющие условия работы деталей.
2. Табличный — допускаемые напряжения принимают по нормам, систематизированным в виде таблиц
(табл. 1 — 7). Этот метод менее точен, но наиболее прост и удобен для практического пользования при проектировочных и проверочных прочностных расчетах.
В работе конструкторских бюро и при расчетах деталей машин применяются как дифференцированный, так и. табличный методы, а также их комбинация. В табл. 4 — 6 приведены допускаемые напряжения для нетиповых литых деталей, на которые не разработаны специальные методы расчета и соответствующие им допускаемые напряжения. Типовые детали (например, зубчатые и червячные колеса, шкивы) следует рассчитывать по методикам, приводимым в соответствующем разделе справочника или специальной литературе.
Приведенные допускаемые напряжения предназначены для приближенных расчетов только на основные нагрузки. Для более точных расчетов с учетом дополнительных нагрузок (например, динамических) табличные значения следует увеличивать на 20 — 30 %.
Допускаемые напряжения даны без учета концентрации напряжений и размеров детали, вычислены для стальных гладких полированных образцов диаметром 6-12 мм и для необработанных круглых чугунных отливок диаметром 30 мм. При определении наибольших напряжений в рассчитываемой детали нужно номинальные напряжения σном и τном умножать на коэффициент концентрации kσ или kτ:
1. Допускаемые напряжения*
для углеродистых сталей обыкновенного качества в горячекатаном состоянии
| Марка стали | Допускаемые напряжения **, МПа | |||||||||||||
| при растяжении [σp] | при изгибе [σиз] | при кручении [τкр] | при срезе [τср] | при смятии [σсм] | ||||||||||
| I | II | III | I | II | III | I | II | III | I | II | III | I | II | |
| Ст2 Ст3 Ст4 Ст5 Ст6 | 115 125 140 165 195 | 80 90 95 115 140 | 60 70 75 90 110 | 140 150 170 200 230 | 100 110 120 140 170 | 80 85 95 110 135 | 85 95 105 125 145 | 65 65 75 80 105 | 50 50 60 70 80 | 70 75 85 100 115 | 50 50 65 65 85 | 40 40 50 55 65 | 175 190 210 250 290 | 120 135 145 175 210 |
* Горский А.И.. Иванов-Емин Е. Б.. Кареновский А. И. Определение допускаемых напряжений при расчетах на прочность. НИИмаш, М., 1974.
** Римскими цифрами обозначен вид нагрузки: I — статическая; II — переменная, действующая от нуля до максимума, от максимума до нуля (пульсирующая); III — знакопеременная (симметричная).
2. Механические свойства и допускаемые напряжения
углеродистых качественных конструкционных сталей
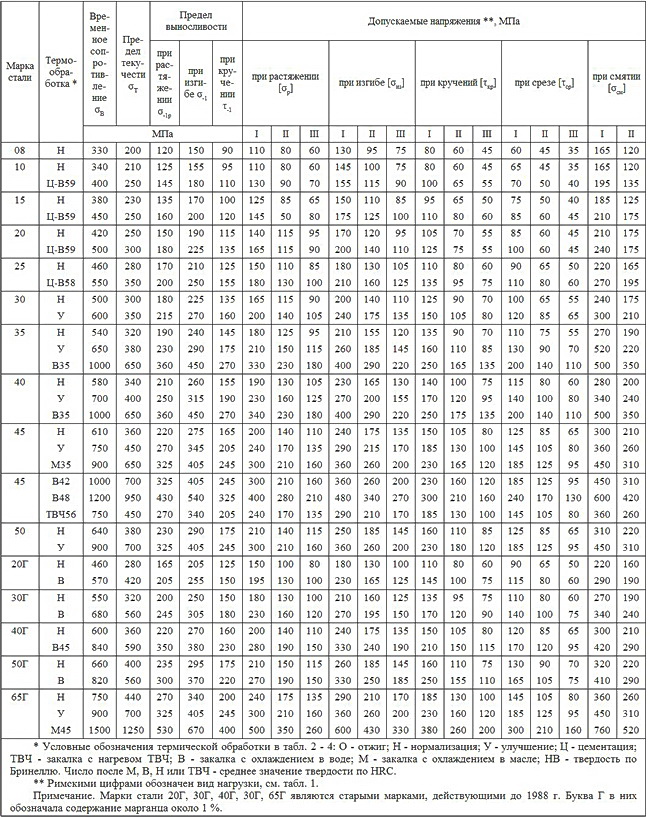
3. Механические свойства и допускаемые напряжения
легированных конструкционных сталей
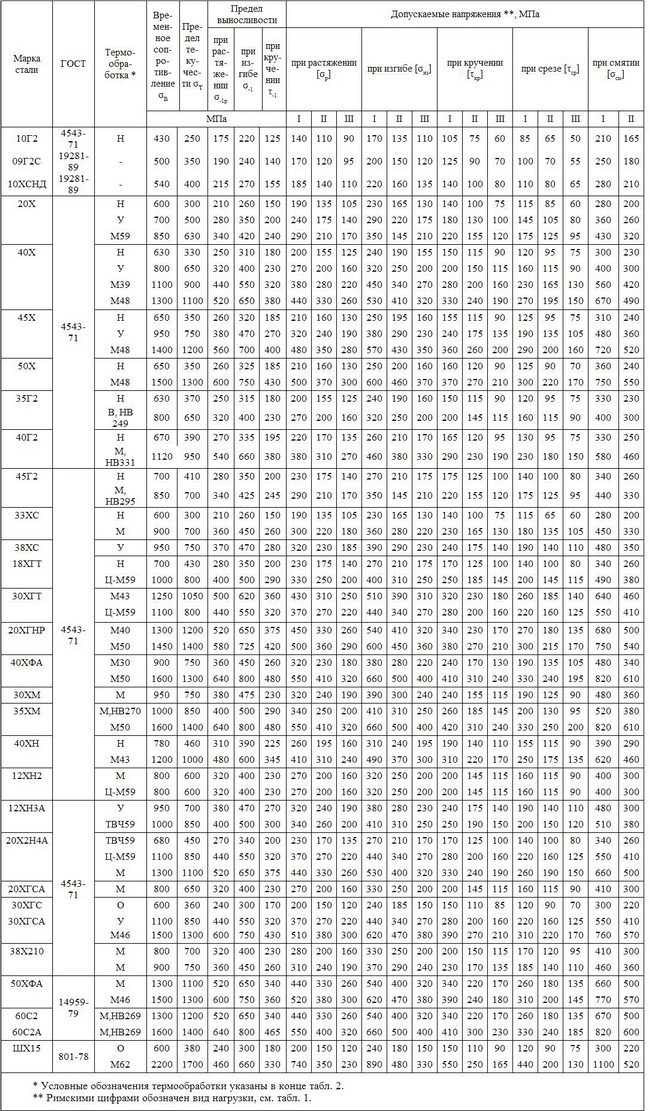
4. Механические свойства и допускаемые напряжения
для отливок из углеродистых и легированных сталей
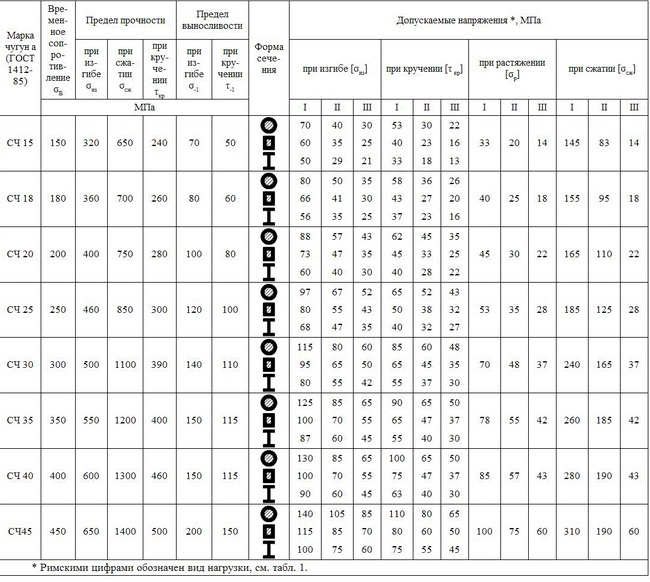
5. Механические свойства и допускаемые напряжения
для отливок из серого чугуна
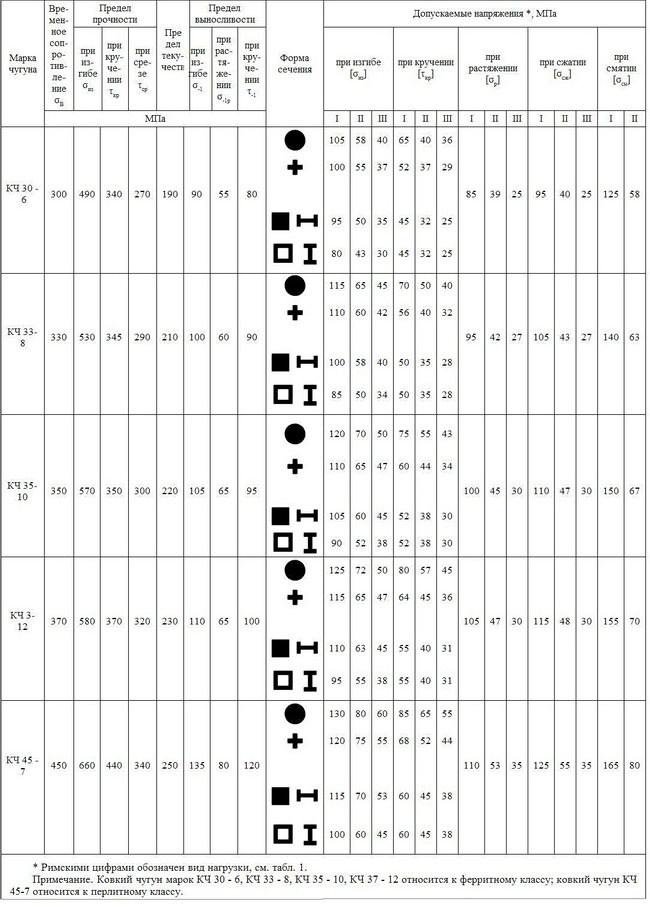
6. Механические свойства и допускаемые напряжения
для отливок из ковкого чугуна
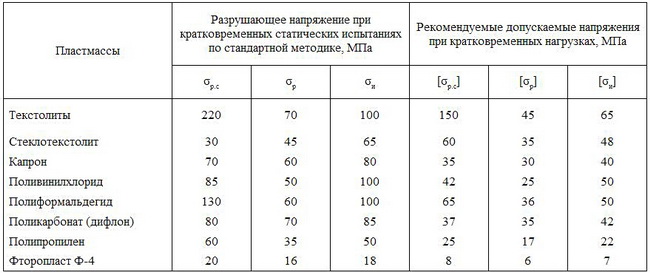
7. Допускаемые напряжения для пластмассовых деталей
Для пластичных (незакаленных) сталей при статических напряжениях (I вид нагрузки) коэффициент концентрации не учитывают. Для однородных сталей (σв > 1300 МПа, а также в случае работы их при низких температурах) коэффициент концентрации, при наличии концентрации напряжения, вводят в расчет и при нагрузках I вида (k > 1). Для пластичных сталей при действии переменных нагрузок и при наличии концентрации напряжений эти напряжения необходимо учитывать.
Для чугунов в большинстве случаев коэффициент концентрации напряжений приближенно принимают равным единице при всех видах нагрузок (I — III). При расчетах на прочность для учета размеров детали приведенные табличные допускаемые напряжения для литых деталей следует умножать на коэффициент масштабного фактора, равный 1,4 . 5.
Приближенные эмпирические зависимости пределов выносливости для случаев нагружения с симметричным циклом:
Механические свойства и допускаемые напряжения антифрикционного чугуна:
— предел прочности при изгибе 250 ÷ 300 МПа,
— допускаемые напряжения при изгибе: 95 МПа для I; 70 МПа — II: 45 МПа — III, где I. II, III — обозначения видов нагрузки, см. табл. 1.
Ориентировочные допускаемые напряжения для цветных металлов на растяжение и сжатие. МПа:
— 30. 110 — для меди;
— 60. 130 — латуни;
— 50. 110 — бронзы;
— 25. 70 — алюминия;
— 70. 140 — дюралюминия.
Источник
Онлайн калькулятор по определению допускаемых напряжений материалов: сталей и сплавов алюминия, меди и титана.
Калькулятор онлайн определяет расчетные допускаемые напряжения σ в зависимости от расчетной температуры для различных марок материалов следующих типов: углеродистая сталь, хромистая сталь, сталь аустенитного класса, сталь аустенито-ферритного класса, алюминий и его сплавы, медь и ее сплавы, титан и его сплавы согласно ГОСТ-52857.1-2007 [1].
| Исходные данные: | |
| Расчетная температура среды Т, °С | |
| Тип материала | углеродистая сталь хромистая сталь сталь аустенитного класса сталь аустенито-ферритного класса алюминий и его сплав медь и ее сплавы титан и его сплавы |
| Марка материала | |
| Решение: | |
| Допускаемое напряжение материала [σ], МПа | определение допускаемого напряжения |
Помощь на развитие проекта premierdevelopment.ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
Допускаемые напряжения были определены согласно ГОСТ-52857.1-2007 [1].
для углеродистых и низколегированных сталей
для жаропрочных, жаростойких и коррозионно-стойких сталей аустенитного класса
Для расчетного срока эксплуатации до 2*10 5 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент 0,9 при температуре Re/20 — минимальное значение предела текучести при температуре 20 °C, МПа; Rр0,2/20 — минимальное значение условного предела текучести при остаточном удлинении 0,2% при температуре 20 °С, МПа. допускаемое
напряжение — наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы. Значение допускаемого напряжения устанавливается путем деления предела прочности, предела текучести и пр. на величину, большую единицы, называемую коэффициентом запаса. расчетная
температура — температура стенки оборудования или трубопровода, равная максимальному среднеарифметическому значению температур на его наружной и внутренней поверхностях в одном сечении при нормальных условиях эксплуатации (для частей корпусов ядерных реакторов расчетная температура определяется с учетом внутренних тепловыделений как среднеинтегральное значение распределения температур по толщине стенки корпуса (ПНАЭ Г-7-002-86, п.2.2; ПНАЭ Г-7-008-89, прил.1).
- [1],п.5.1. Расчетную температуру используют для определения физико-механических характеристик материала и допускаемых напряжений, а также при расчете на прочность с учетом температурных воздействий.
- [1],п.5.2. Расчетную температуру определяют на основании теплотехнических расчетов или результатов испытаний, или опыта эксплуатации аналогичных сосудов.
- За расчетную температуру стенки сосуда или аппарата принимают наибольшую температуру стенки. При температуре ниже 20 °С за расчетную температуру при определении допускаемых напряжений принимают температуру 20 °С.
- [1],п.5.3. Если невозможно провести тепловые расчеты или измерения и если во время эксплуатации температура стенки повышается до температуры среды, соприкасающейся со стенкой, то за расчетную температуру следует принимать наибольшую температуру среды, но не ниже 20 °С.
- При обогреве открытым пламенем, отработанными газами или электронагревателями расчетную температуру принимают равной температуре среды, увеличенной на 20 °С при закрытом обогреве и на 50 °С при прямом обогреве, если нет более точных данных.
- [1],п.5.4. Если сосуд или аппарат эксплуатируются при нескольких различных режимах нагружения или разные элементы аппарата работают в разных условиях, для каждого режима можно определить свою расчетную температуру (ГОСТ-52857.1-2007, п.5).
Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
Источник
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.
Внутренние силовые факторы, метод сечений.
При действии на тело внешних сил внутри тела возникают силы сопротивления, которые называются внутренними силовыми факторами.
При различных видах деформаций возникают определённые внутренние силовые факторы. Всего при различных видах деформаций возникает шесть внутренних силовых факторов, которые характеризуют все виды деформаций, существующие в природе.
1. N – продольная сила, возникает при деформации растяжение и сжатие.
Это поперечные силы, возникают при деформации сдвиг.
Это изгибающие моменты, возникают при деформации изгиб.
6. МZ =Т – крутящий момент, возникает при деформации кручение.
Чтобы вычислить внутренние силовые факторы, применяется метод сечений, который заключается в том, что тело мысленно рассекается на две части, одна часть отбрасывается, а другая рассматривается и вместо отброшенной части прикладываются внутренние силовые факторы. Значения внутренних силовых факторов вычисляются из уравнений равновесия.
Нормальное напряжение.
Касательное напряжение.
Напряжение – это мера интенсивности действия внутренних сил.
При действии на конструкцию внешней нагрузки в материале конструкции возникает механическое напряжение, которое характеризует интенсивность внутренних сил. Если нагрузку постепенно увеличивать, то значение напряжения тоже будет увеличиваться, и когда оно достигнет какого – то критического значения, произойдёт разрушение материала.
Полное напряжение р разложим на две оси, одна из них перпендикулярна к поперечному сечению конструкции, другая параллельна.
σ – нормальное напряжение, возникает при деформации растяжение или сжатие, всегда направлено перпендикулярно к поперечному сечению конструкции.
τ – касательное напряжение, возникает при деформации сдвиг, всегда направлено параллельно к поперечному сечению конструкции.
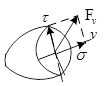
Рассмотрим нормальное напряжение. Оно вычисляется по следующей формуле:
где S – площадь поперечного сечения конструкции
Единица измерения напряжения (Н/м2 ) =Па
Так как величина Па очень маленькая, то на практике применяют величину
[σ] – допускаемое нормальное напряжение, каждый материал имеет своё значение.
Чтобы обеспечить прочность конструкции, значение напряжения не должно превышать допускаемого, иначе может произойти разрушение материала.
Приблизительные значения допускаемого нормального напряжения для некоторых материалов:
Легированные высококачественные стали: [σ] = 400 МПа и выше
Рассмотрим касательное напряжение. Оно вычисляется по следующей формуле:
[τ] – допускаемое касательное напряжение, каждый материал имеет своё значение.
Для большинства материалов [τ] = 0,6•[σ]
Деформации и перемещения.
Деформация – это изменение формы и объёма тела.
Деформация бывает упругой и пластичной. При упругой деформации тело полностью восстанавливает свою первоначальную форму и размеры после снятия нагрузки, а при пластичной нагрузке этого не происходит.

Деформация также бывает линейной и угловой.
Расчёт на прочность при растяжении и сжатии.
Условие прочности при растяжении и сжатии – нормальное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при растяжении и сжатии выглядит следующим образом:
Расчёт на прочность при растяжении и сжатии можно также проводить через коэффициент запаса прочности
n – коэффициент запаса прочности
[n] – минимально допустимый коэффициент запаса прочности
При статической нагрузке [n] =1,5
Чтобы обеспечить прочность, должно соблюдаться условие:
Температурные напряжения.
При нагреве или охлаждении металлического стержня его длина изменяется. Удлинение от действия температуры вычисляется по формуле
где α – коэффициент температурного расширения, величина табличная.
Например, для стали α = 1,25·10 – 5 1/град
Δt – изменение температуры
В связи с нагревом или охлаждением в металлических конструкциях могут возникнуть дополнительные температурные напряжения. Вычислив удлинение от действия температуры, из формулы (3) можно вычислить температурные напряжения.
Монтажные напряжения.
Часто встречаются случаи, когда стержневые элементы конструкций изготавливаются короче или длиннее проектной длины. При монтаже конструкции такие стержни приходится растягивать или укорачивать, что приводит к возникновению дополнительных монтажных напряжений. Эти напряжения можно вычислить из формулы (3).
16. Сдвиг (основные понятия и определения), расчёт на прочность при сдвиге.
Сдвиг – это такой вид деформации, при котором в поперечном сечении бруса возникает следующий внутренний силовой фактор – поперечная сила Q.
Деформация сдвиг ещё называется срез.
При сдвиге действует касательное напряжения τ, которое вычисляется по следующей формуле
Деформация при сдвиге называется углом сдвига γ, вычисляется по следующей формуле
где G – модуль упругости ΙΙ рода, или модуль сдвига, характеризует жесткость бруса при сдвиге, величина табличная.
Для большинства материалов G = 0,4•E
Величина GS называется жёсткостью при сдвиге.
Подставим выражение (7) в выражение (8), получим
Выражения (9) и (10) являются законом Гука при сдвиге, который формулируется следующим образом: напряжение прямо пропорционально углу сдвига.
Единица измерения угла сдвига – радиан, можно перевести в градусы.
Условие прочности при сдвиге – касательное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при сдвиге выглядит следующим образом:
Примеры расчёта конструкций, работающих на сдвиг.
Рассмотрим заклёпочное соединение, на которое действуют сила F, направленная перпендикулярно осям заклёпок.
Условие прочности такого соединения имеет вид:
S – площадь поперечного сечения всех заклёпок;
где S1 – площадь поперечного сечения одной заклёпки
Рассмотрим сварное соединение внахлёстку, на которое действует сила F.
Условие прочности такого соединения имеет вид:
S – расчётная площадь сварного шва
где k – катет сварного шва
L – длина сварного шва по длине соединения
b – длина сварного шва по ширине соединения
Кинематические пары.
Примеры кинематических пар в зависимости от классов.
Кинематическая пара – соединение двух соприкасающихся звеньев, допускающее их относительное движение.
Элемент кинематическая пары – совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару
Кинематические пары различают и классифицируют по различным признакам.
1) По числу связей, налагаемых на относительное движение звеньев.
Всякое свободно движущееся в пространстве абсолютно твердое тело обладает шестью степенями свободы или шестью видами независимых возможных движений. Вхождение двух звеньев в кинематическую пару налагает на их относительное движение некоторые ограничения или условия связи; класс кинематической пары (номер класса совпадает с числом условий связи S) всегда находится в пределах от 1 до 5, число оставшихся подвижностей H дополняет число связей до шести, т.е. 
На рис. 3 представлены примеры кинематических пар 1 – 5 классов.
2) По характеру контакта звеньев различают пары низшие (требуемое относительное движение звеньев можно получить постоянным соприкасанием их элементов по поверхности) и высшие (требуемое относительное движение можно получить только соприкасанием их элементов по линиям и в точках). Например, трехподвижная пара по
рис. 3, в – низшая, а четырехподвижная по рис. 3, б – высшая.
3) По области относительного движения звеньев пары могут быть плоскими (траектории всех точек в относительном движении звеньев – плоские кривые, расположенные в параллельных плоскостях) и пространственными.
Плоская одноподвижная пара может быть либо вращательной (шарниром – рис. 3, д), либо поступательной (рис. 3, е); пространственная пара может быть, например, винтовой (одноподвижная), цилиндрической (двухподвижная), сферической (двух- и трехподвижная) и т.д.
Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.
 |  |
| а – пятиподвижная пара (1 класс) | б – четырехподвижная пара (2 класс) |
 |  |
| в – трехподвижная пара (3 класс) | г – двухподвижная пара (4 класс) |
 |  |
| д – одноподвижная вращательная пара (5 класс) | е – одноподвижная поступательная пара (5 класс) |
| Рис. 3 |
Кинематические цепи.
Систему звеньев, связанных между собой кинематическими парами, называют кинематической цепью.
Классификация кинематических цепей
1) По области движения звеньев цепи бывают плоские (траектории движения точек всех звеньев –– плоские кривые, лежащие в параллельных плоскостях) и пространственные.
2) По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем в две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.
3) По признаку наличия в кинематических цепях замкнутых контуров цепи могут быть замкнутыми и незамкнутыми; в замкнутой цепи каждое звено входит не менее, чем в две кинематические пары.
Некоторые дополнительные определения:
обобщенная координата механизма – каждая из независимых координат, определяющих положение всех звеньев механизма относительно стойки;
число степеней свободы (степень подвижности) механизма – число независимых вариаций обобщенных координат механизма;
начальное звено – звено, которому приписывается одна или несколько обобщенных координат механизма;
входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев;
выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм.
Методы силового анализа.
Силовой расчет механизмов без учета трения в кинематических парах допускает применение как аналитических, так и графо – аналитических методов.
В настоящем пособии предпочтение отдано графо – аналитическому методу планов сил.
Поскольку векторный план представляет собой графическое изображение векторного равенства, то при простой форме векторных силовых многоугольников их аналитическая обработка достаточно проста и позволяет рассчитать точные силовые соотношения для заданных положений механизмов.
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.
Источник