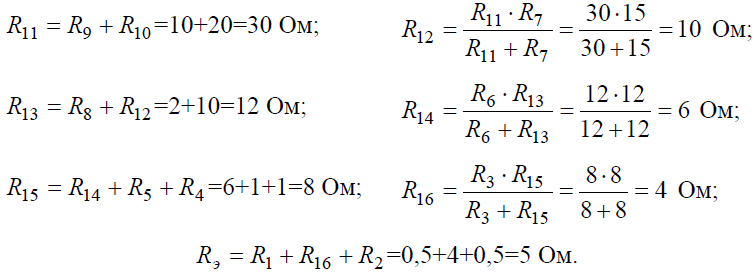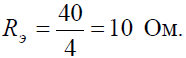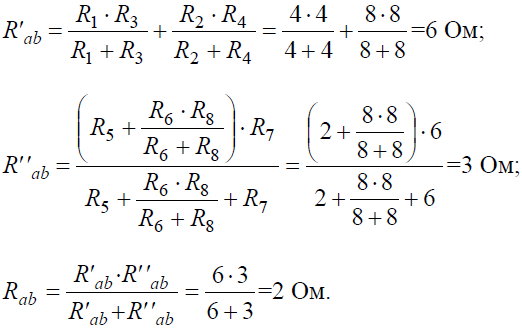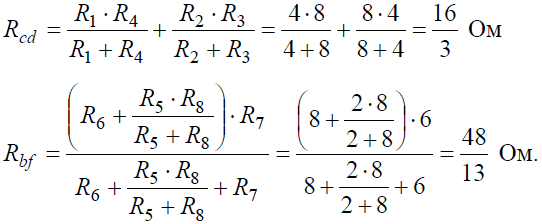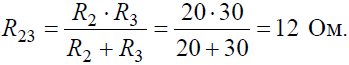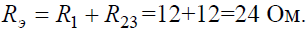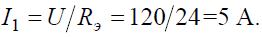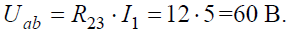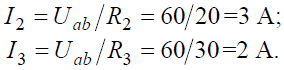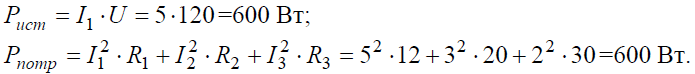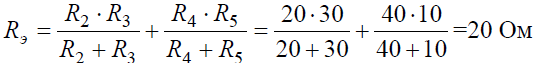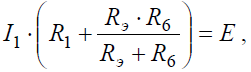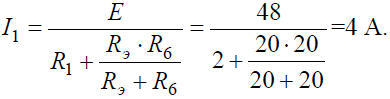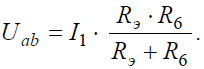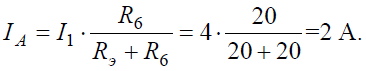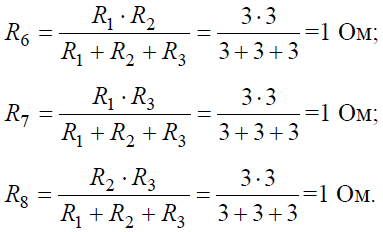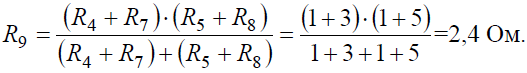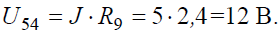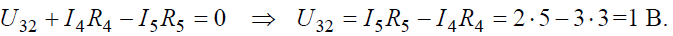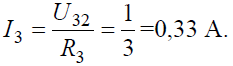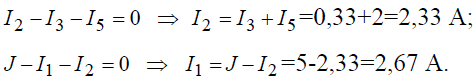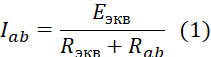Как найти эквивалентное напряжение цепи

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Расчет электрических цепей постоянного тока методом эквивалентных преобразований

Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.

На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.

Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.

Преобразуют параллельные и последовательные соединения элементов, соединение «звезда » в эквивалентный «треугольник » и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.

Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований

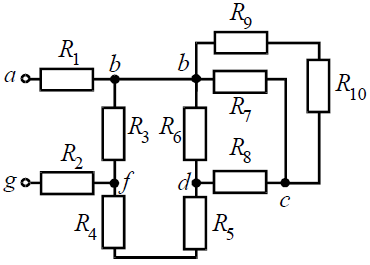
Задача 1. Для цепи (рис . 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R₁ = R₂ = 0,5 Ом, R₃ = 8 Ом, R₄ = R₅ = 1 Ом, R₆ = 12 Ом, R₇ = 15 Ом, R₈ = 2 Ом, R₉ = 10 Ом, R₁₀= 20 Ом.

Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:

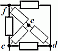
Задача 2. Для цепи (рис . 2, а), определить входное сопротивление если известно: R₁ = R₂ = R₃ = R₄= 40 Ом.

Рис. 2

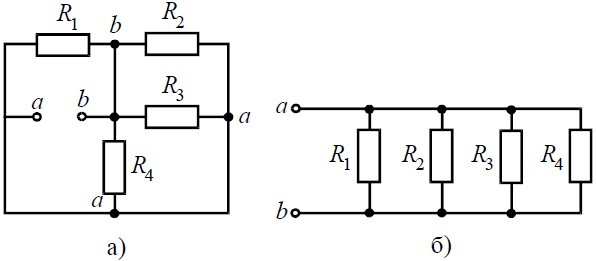
Исходную схему можно перечертить относительно входных зажимов (рис . 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:

где R – величина сопротивления, Ом;

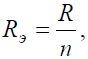
n – количество параллельно соединенных сопротивлений.

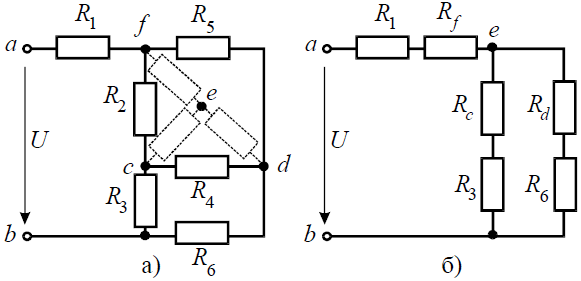
Преобразуем соединение «треугольник » f−d−c в эквивалентную «звезду ». Определяем величины преобразованных сопротивлений (рис . 3, б):

По условию задачи величины всех сопротивлений равны, а значит:

На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:

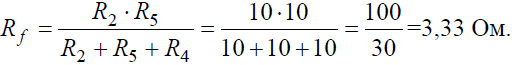
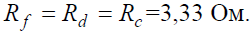
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:

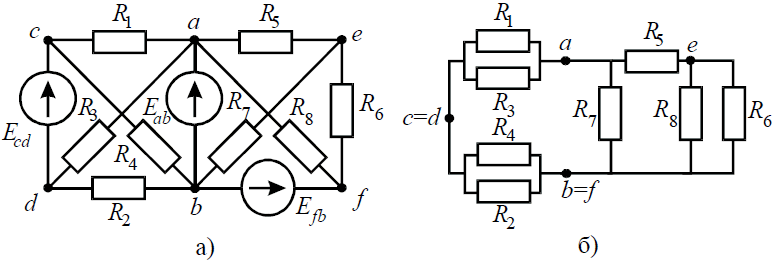
Задача 4. В заданной цепи (рис . 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R₁ = 4 Ом, R₂ = 8 Ом, R₃ =4 Ом, R₄ = 8 Ом, R₅ = 2 Ом, R₆ = 8 Ом, R₇ = 6 Ом, R₈ =8 Ом.

Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.

Ветвь a−b разрывают, и т.к. сопротивление R_a–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис . 4, б):

Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей R_cd и R_bf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает ») из схемы сопротивления R₁, R₂, R₃, R₄ в первом случае, и R₅, R₆, R₇, R₈ во втором случае.

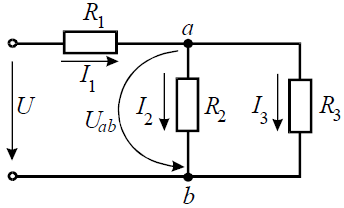
Задача 5. В цепи (рис . 5) определить методом эквивалентных преобразований токи I₁, I₂, I₃ и составить баланс мощностей, если известно: R₁ = 12 Ом, R₂ = 20 Ом, R₃ = 30 Ом, U = 120 В.

Эквивалентное сопротивлениедля параллельно включенных сопротивлений:

Эквивалентное сопротивление всей цепи:

Ток в неразветвленной части схемы:

Напряжение на параллельных сопротивлениях:

Токи в параллельных ветвях:

Баланс мощностей:

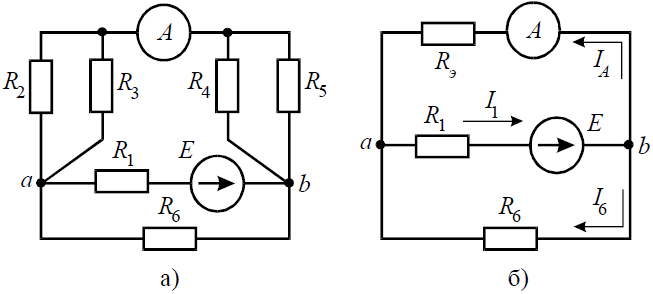
Задача 6. В цепи (рис . 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R₁ = 2 Ом, R₂ = 20 Ом, R₃ = 30 Ом, R₄ = 40 Ом, R₅ = 10 Ом, R₆ = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.

Если сопротивления R₂, R₃, R₄, R₅ заменить одним эквивалентным сопротивлением R_Э, то исходную схему можно представить в упрощенном виде (рис . 6, б).

Величина эквивалентного сопротивления:

Преобразовав параллельное соединение сопротивлений R_Э и R₆ схемы (рис . 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:

Напряжение на зажимах параллельных ветвей U_ab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием R_Э и R₆:

Тогда амперметр покажет ток:

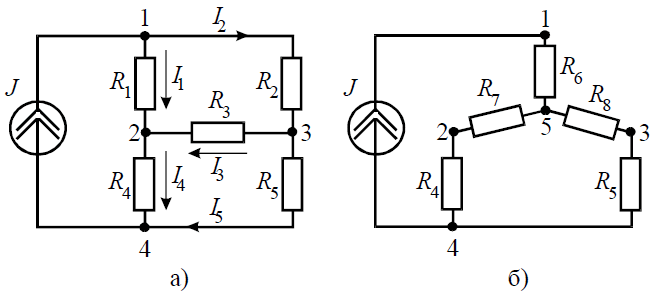
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис . 7, а), если R₁ = R₂ = R₃ = R₄ = 3 Ом, J = 5 А, R₅ = 5 Ом.

Преобразуем «треугольник » сопротивлений R₁, R₂, R₃ в эквивалентную «звезду » R₆, R₇, R₈ (рис . 7, б) и определим величины полученных сопротивлений:

Преобразуем параллельное соединение ветвей между узлами 4 и 5

Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:

Возвращаясь к исходной схеме, определим напряжение U₃₂ из уравнения по второму закону Кирхгофа:

Тогда ток в ветви с сопротивлением R₃ определится:

Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:

Метод эквивалентных преобразований

Источник

Метод эквивалентного генератора

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.

Алгоритм состоит из следующих шагов:

1. Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
2. Рассчитывается эквивалентная эдс генератора.
3. Определяется эквивалентное сопротивление генератора.
4. По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.

Метод эквивалентного генератора: примеры решения

Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).

Рис. 1. Метод эквивалентного генератора

Допустим, что необходимо рассчитать ток I_ab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.

Рис. 2. Эквивалентная электрическая схема

После преобразования ток через резистор R_ab (R4) определяется по формуле

Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).

Рис. 3. Режим холостого хода генератора

Для представленной схемы напряжение Еэкв будет равно

Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).

Рис. 4. Схема без источника эдс

Эквивалентное сопротивление полученной схемы определяется по формуле

Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).

Источник