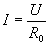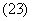Как определить абсолютную погрешность измерения напряжения вольтметром

Погрешности измерений

Общие сведения об измерениях. Погрешности измерений и средств измерений

Общие сведения об измерениях

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.

Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.

Погрешности измерений

Погрешность является одной из основных характеристик средств измерений.

Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.

Абсолютная погрешность Δ_a прибора есть разность между показанием прибора а_х и истинным значением а измеряемой величины, т.е.

Абсолютная погрешность, взятая с обратным знаком, называется поправкой.

Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна

Приведенная погрешность γ_П есть выраженное в процентах отношение абсолютной погрешности Δ_a к нормирующему значению а_пр

Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).

Погрешности средств измерений

Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.

Класс точности прибора (например, амперметра) дается выражением

При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.

По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:

В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:

(α = 1) 10; 15; 20; 25; 40; 50; 60.

Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.

Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.

Примеры решения задач

Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.

1. Класс точности указывают просто числом предпочтительного рода, например, 0,5. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.

Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)

постоянна и равна классу точности прибора.

Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)

уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.

Абсолютная погрешность однократного измерения

постоянна на всех отметках рабочей части шкалы прибора.

По условию задачи: U_изм = U_i = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; U_пр = 30 В – предел шкалы вольтметра.

Наибольшая абсолютная погрешность вольтметра

Источник

Как определить абсолютную погрешность измерения напряжения вольтметром

Метод и средства для измерения напряжения и тока.

При измерении напряжения и тока используют прямые и косвенные способы. Прямые измерения основаны на сравнении измеряемой величина с мерой этой величины или на непосредственной оценке измеряемой величины по отчетному устройству измерительного прибора. Косвенные измерения основаны на прямых измерениях другой величины, функционально связанной с измеряемой величиной. Например, косвенное измерение тока выполняют при помощи вольтметра, измеряющего напряжение на известном сопротивлении R0, и расчете тока по формуле

Погрешность косвенного метода измерения зависит от погрешности прямого измерения и погрешности расчета по функциональной зависимости (23). Сопротивление, используемое при косвенном измерении тока, называют шунтом. Дополнительная погрешность при косвенных измерениях обусловлена перераспределением тока между шунтом и вольтметром при изменении температуры окружающей среды. Для снижения температурной погрешности применяют специальные схемы компенсации,

В зависимости от рода тока приборы делят на четыре группы;

1) вольтметры постоянного напряжения (группа В2),
2) вольтметры переменного напряжения (группа ВЗ),
3) вольтметры импульсного напряжения (группа В4),
4) вольтметры селективные (группа В6).

Универсальные приборы, предназначенные для измерения постоянного и импульсного напряжения и тока, выделены в группу В7.

Программа работы

1. Определение основной погрешности, вариация показаний и поправку вольтметра.
2. Определение чувствительности и цены деления вольтметра.
3. Определение входного сопротивления вольтметра.
4. Определение частотного диапазона вольтметра.
5. Исследование влияния формы напряжения на показание вольтметра.
6. Определение погрешности при прямых и косвенных измерениях тока.

Порядок выполнения работы.

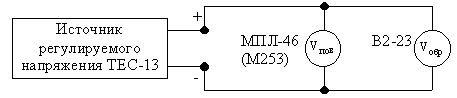
1. Определение основной погрешности, вариация показаний и поправки вольтметра выполняют по схеме, изображенной на рис. 1. В качестве поверяемого прибора используют вольтметр типа МПЛ-46, а образцовый служит цифровой вольтметр типа В2-23. Перед проведением измерений прибор В2-23 включить в сеть и выждать 10…15 мин. Затем произвести установку нуля и калибровку вольтметра И2-23 в соответствии с инструкцией по пользованию прибором. Кроме того, необходимо выполнить установку нуля вольтметра МПЛ-46, пользуясь корректором.

Для выполнения п.1 программы поверяемый вольтметр МПЛ-46 устанавливают на диапазон 15 В и измеряют напряжение на всех оцифрованных делениях шкалы, изменяя входное напряжение регулируемого источника ТЕС-13. Измерение напряжения на каждом оцифрованном делении шкалы МПЛ-46 производят дважды: один раз при возрастании напряжения (показание образцового вольтметра U’_обр), а второй раз при убывание напряжения (показание образцового вольтметра U’’_обр). При этом на образцовом вольтметре В2-23 необходимо выбрать поддиапазон, обеспечивающий не менее трех значащих цифр. Результаты измерений занести в ф.1.

Действительные значения на оцифрованных делениях шкалы поверяемого вольтметра определяют как среднее значение двух измерений U_ср=(U’_обр+U’’_обр)/2.
Расчет погрешности измерений выполняют по формулам:
Абсолютная погрешность U=U_пов-U_ср,
Относительная погрешность 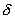=(U/ U_пов)*100%,
Приведенная погрешность _п=(U/ U_ном) *100%,
где U_ном=15 В – номинальное значение напряжения поверяемого.
Вариацию показаний вольтметра определяют по формулам:
Абсолютное значение вариации U=U’_обр-U’’_обр,
Приведенное значение вариации _в=(U_обр/ U_ном)*100%,
Поправку вольтметра вычисляют по формуле П=-U.
Из полученных значений _п и _в необходимо выбрать наибольшее и сравнить их с классом точности К_u поверяемого вольтметра. Если _{п макс} и _{в макс} окажутся больше К_u, то поверяемый вольтметр нельзя использовать с указанным классом точности.

Источник

Оценка абсолютной погрешности прямых измерений

Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.

Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.

Все остальные погрешности являются случайными.

Промахи — грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.

Приборные погрешности определяются двумя факторами:

1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.

Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g — класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;

2. ценой делений шкалы прибора:

(Dx) ц.д.= h,

где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда , который предписывает следующий образ действий, если физическая величина х измерена n раз:

1) имея х1 , …,хn – значений измеряемой величины х, выбираем из хmax и хmin и находим среднее значение х:
;
2) находим абсолютную погрешность Dxр =
3) Записываем результат в виде: с , где a — доверительная вероятность того, что истинное значение измеренной величины находится на отрезке .
Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:

1) Вы измерили и получили несколько i = 1. m значений случайной
величины i. Сначала исключаем промахи, то есть заведомо неверные
результаты.
2) По оставшимся n значениям определяем среднее значение величины :
i
3) Определяем среднеквадратичную погрешность среднего значения :

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины (доверительный интервал)
D= tan s
6) Записываем результат
= ( ± D ) с указанием доверительной вероятности a.

В научных статьях обычно приводят доверительный интервал
D = s ,

соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее — погрешность) эксперимента (подробнее см. в работе [1]).

Источник