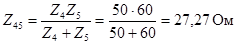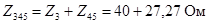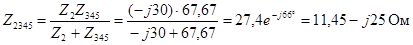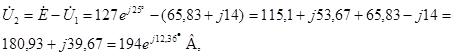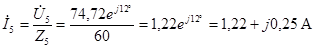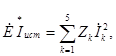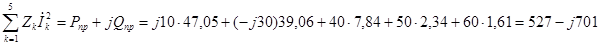Векторная диаграмма токов в маткаде
Phasor Diagrams in MathCAD
Построение векторной диаграммы напряжения в MathCad. векторная диаграмма токов и напряжений, векторная диаграмма токов и топографическая диаграмма напряжений, векторные диаграммы токов и напряжений, как построить векторную диаграмму токов, mathcad уроки, векторные диаграммы, построение векторной диаграммы, mathcad, чтение векторной диаграммы токов и напряжений, как построить топографическую диаграмму потенциалов в mathcad, программы для построения диаграмм, построение векторных диаграмм токов и напряжений, сдвиг фаз векторная диаграмма.
материалы для построения векторной диаграммы на сайте:
Видео Построение векторной диаграммы напряжения в MathCad (Phasor Diagrams in MathCAD) канала Евгений Осинцев
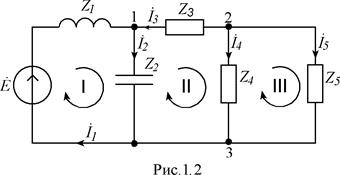
Рассмотрим ход выполнения задания на примере варианта 30-13-1. Изображение каждого элемента на схеме должно соответствовать его характеру ( 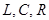
Комплексы сопротивлений элементов имеют значения 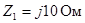
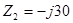
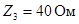
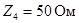
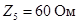
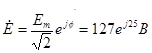
1. Составление системы уравнений по законам Кирхгофа.
Выбираем направления токов в ветвях и направления обхода контуров. Составим систему уравнений для комплексов действующих токов и напряжений:
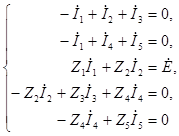
Подставляя данные, запишем систему уравнений (1.1) в матричной форме 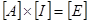
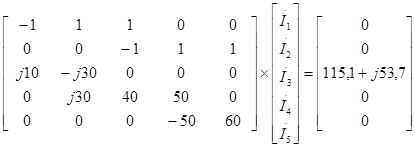
где квадратная матрица [A]– обобщенная матрица коэффициентов, [I] – матрица токов ветвей цепи, столбец правой части [E] – вектор входных воздействий.
Составленное матричное уравнение (1.2) решаем с помощью прикладной программы MathCAD. Результаты вычислений приводиться в пояснительной записке домашнего задания. Напряжения на элементах определяются по закону Ома в комплексной форме.
2. Результаты расчетов занести в табл. 1.3.
| Расчетная Величина | Результаты расчета программой MathCAD в действующих значениях | Мгновенные значения | Результаты расчета методом эквивалентных преобразований | |
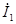 | А | 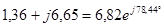 | 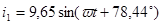 | 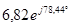 |
| … | … | … | … | … |
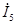 | А | 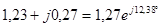 | 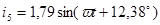 | 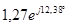 |
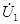 | В | 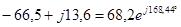 | 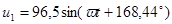 | 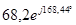 |
| … | . | … | … | … |
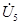 | В | 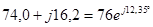 | 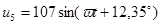 | 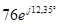 |
3. Расчет электрической схемы методом эквивалентных преобразований.
С помощью метода эквивалентных преобразований находим эквивалентное (входное) сопротивление цепи. Будем определять сопротивления участков цепи (используем составные индексы, состоящие из индексов участвующих элементов). При этом все результаты целесообразно записывать и в показательной и алгебраической формах, поскольку для умножения и деления удобнее показательная, а для суммирования и вычитания – алгебраическая форма.
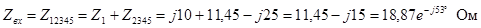
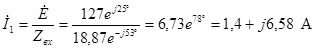
Тогда 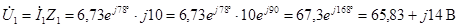
Дальнейшие шаги расчета можно проводить двумя способами: по закону Ома или законам Кирхгофа. Можно пользоваться любым методом, а можно пользоваться и обеими одновременно, что позволит сравнивать результаты с целью текущей самопроверки.
по закону Ома
(незначительные отклонения допустимы, поскольку расчет производился с округлением результата после каждого шага).
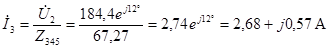
или
или
или 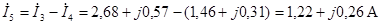
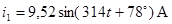
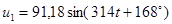
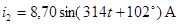
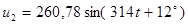
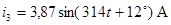
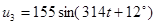
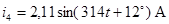
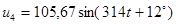
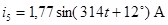
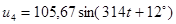
Полученные методом эквивалентных преобразований значения токов сравниваем с результатами расчета с помощью прикладной программы MathCAD.
4. Проверка баланса активных и реактивных мощностей.
Проверка баланса мощностей проводится в соответствии с уравнением
где 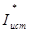
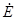
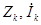
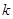
Для рассмотренного варианта:
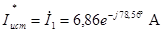
Определяем полную мощность источника:
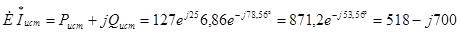
Далее определяем полную мощность приемников цепи:
Проводим оценку баланса по формулам
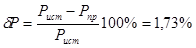
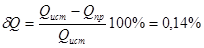
Полученное расхождение находится в пределах погрешности вычислений.
5. Определение показаний приборов.
Амперметр показывает действующее значение тока IA=I2= 6,25 А. Вольтметр – действующее напряжения Uv = U4 = 76.5 В.
Показание ваттметра определяется произведением действующих значений измеряемого напряжения и измеряемого тока, умноженным на косинус сдвига фаз между ними:
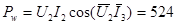
6. Построение векторной диаграммы токов и напряжений.
Для построения векторной диаграммы (рис 1.3) можно воспользоваться любой из форм представления комплексов действующих значений токов и напряжений.
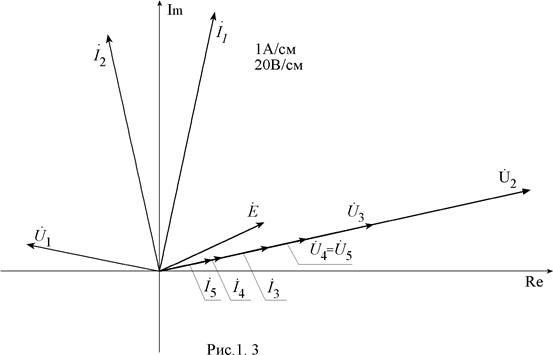 |
Векторная диаграмма токов должна удовлетворять уравнениям по первому закону Кирхгофа, векторная диаграмма напряжений – уравнениям по второму закону Кирхгофа.
Векторная диаграмма строится, на миллиметровке с использованием масштабов, соответствующих ГОСТ. Желательно выделять токи и напряжения разными цветами. Заметим, что пользуясь правилами сложения векторов, можно по векторной диаграмме легко проверить выполнение уравнений (1.1), составленных по законам Кирхгофа при подстановке в них рассчитанных выше результатов.
7. Определение сопротивления каждого элемента при изменении частоты в n раз проводим с учетом зависимостей индуктивного и емкостного сопротивлений от частоты.
8. Определение тока в одной из ветвей методом эквивалентного генератора (Э.Г.).
Номер ветви, ток в которой следует определить методом Э.Г., задается преподавателем. Определение тока методом Э.Г. произведем на примере второй ветви схемы по тому же (рассмотренному выше) варианту 30-13-1.
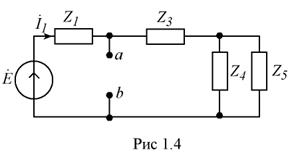
В соответствии с сущностью метода, схема Э.Г. имеет вид, приведенный на рис. 1.4.
В этой схеме интересующая нас нагрузка присоединяется к точкам a и b. Пользуясь результатами, полученными выше, имеем 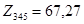
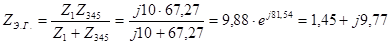
ЭДС Э.Г. отличается от ЭДС источника Е на величину падения напряжения, создаваемого током I, на сопротивлении 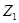
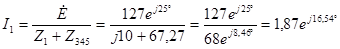
Искомый ток определяется в соответствии со схемой на рис 1.5
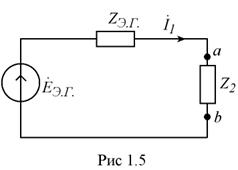
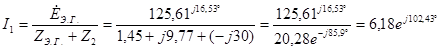
Сравнение этого результата с результатом, полученным ранее, дает расхождение, приемлемое в пределах погрешности вычислений.
Задание 2. РАСЧЕТ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА РАЗЛИЧНЫМИ МЕТОДАМИ
Исходные данные:
В цепи, представленной на рис 1.1 (см. задание 1), действуют два (из пяти возможных) источника синусоидальной ЭДС 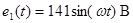
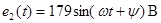
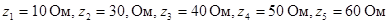
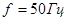
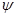
Номер варианта задает преподаватель в виде четырех чисел, например 25 ‑7 ‑ 2 ‑ 3 . Первое число указывает на номер строки в табл. 1, второе число определяет нумерацию сопротивлений (табл. 1) в соответствии с номером строки в таблице 2, третье и четвертое числа указывают номера сопротивлений, последовательно с которыми включены источники 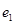
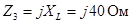
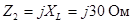
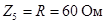
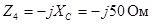
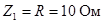
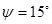
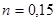
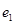
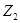
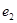
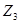
1. Составить и решить на компьютере систему алгебраических уравнений в комплексной форме:
1.2 по методу контурных токов.
2. Значения токов в ветвях и напряжения на всех участках, найденные с помощью законов Кирхгофа, записать в алгебраической и показательной формах. Перейти от комплексов токов и напряжений к их мгновенным значениям. Комплексы действующих контурных токов привести в алгебраической и показательной формах.
3. Найти комплексы действующих значений токов в ветвях в алгебраической и показательной формах. Сравнить результаты, полученные двумя способами.
4. Составить и решить систему алгебраических уравнений в комплексной форме методом узловых потенциалов. Определить токи в ветвях. Сравнить полученные значения токов со значениями, полученными в п.1.
5. Проверить баланс активных мощностей.
6. Определить показания амперметра, вольтметра и ваттметра.
7. Построить векторные диаграммы токов и напряжений.
8. Определить ток в одной из ветвей цепи, не содержащей источника ЭДС, методом эквивалентного генератора (ЭДС эквивалентного генератора найти методом наложения). Сравнить полученное значение тока с его значением, найденным по законам Кирхгофа и методом комплексных токов.
9. Определить сопротивление каждого элемента при изменении частоты в n раз (n задано в табл. 1.1).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 10310 — 

Далее для расчета симметричных составляющих, мы составляем систему из шести уравнений, первые три уравнения мы составляем по второму закону Кирхгофа для схем замещения, и еще три по граничным условиям в месте несимметрии. В нашем случае (в случае обрыва фаз А и С) — I?A=0, U?B=0, I?C=0.
Теперь подставим уравнения (7), (8), (9) в (5), получаем:
Остальные симметричные составляющие токов и напряжений найдутся по вышеприведенным формулам.
Все симметричные составляющие найдены, теперь можно вычислить искомые токи и напряжения:


Программа Mathcad значительно облегчает задачу нахождения токов и напряжений. Для решения системы в Mathcad составим матрицу коэффициентов и матрицу свободных членов.
В результате решения системы получим симметричные составляющие токов и напряжений, по которым найдем искомые токи и напряжения.
Значения, полученные ручным расчетом, совпадают со значениями, полученными в Mathcad, следовательно, система решена верно.
Для построения диаграмм тоже удобно пользоваться программой Mathcad. Вектора можно быстро построить, задавая их матрицами.
Рисунок 3.10 — Векторная диаграмма токов в месте обрыва
Рисунок 3.11 — Векторная диаграмма напряжений в месте обрыва
Источник