Расчёт на прочность стержня болта. Болт затянут, к соединению приложена сдвигающая сила. Болт установлен с зазором и без зазора.
Расчет болта, при установке его с зазором.
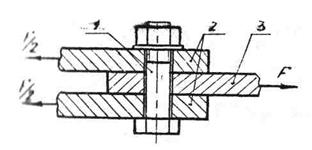
В этом случае болт ставится с зазором в отверстие деталей. Для обеспечения неподвижности соединяемых листов 1, 2, 3 болт затягивают силой затяжки F3. Во избежание работы болта на изгиб его следует затянуть так сильно, чтобы силы трения на стыках деталей были больше сдвигающих сил Fr.
1) Деформация соединяемых деталей не учитывается, то есть детали принимают абсолютно жесткими.
2) Внешние нагрузки передаются от одной детали на другую локально, через зоны, расположенные вокруг болтов.
3) Расчет ведут на предотвращение сдвига деталей по условию неподвижности стыка.
Основным критерием расчета является условие неподвижности стыка.
Обычно силу трения принимают с запасом: Ff= KFr. (К –коэффициент запаса по сдвигу деталей, К = 1,3 – 1,5 при статической нагрузке, К = 1,8 – 2 при переменной нагрузке).
Найдем требуемую затяжку болта. Учтем, что сила затяжки болта может создавать нормальное давление на i трущихся поверхностях
где i – число плоскостей стыка деталей (на рис.52 – i = 2; при соединении только двух деталей i = 1); f – коэффициент трения в стыке (f = 0,15 – 0,2 для сухих чугунных и стальных поверхностей);
Как известно при затяжке болт работает на растяжение и кручение, поэтому прочность болта оценивают по эквивалентному напряжению. Так как внешняя нагрузка не передается на болт, его рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.
Проектировочный расчет болта:
внутренний диаметр резьбы
Расчет болта, с установкой его без зазора.
1) Деформации деталей не учитываются, то есть считают детали абсолютно жесткими.
2) Внешние нагрузки передаются с одной детали на другую локально, через зоны, расположенные вокруг болтов.
3) Силы трения, связанные с затяжкой болтов, не учитываются.
4) Основным критерием расчета является условие неподвижности стыка.
5) При установке болта без зазора неподвижность обеспечивается сопротивлением болта срезу и смятию.
В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности данного соединения не учитывают силы трения в стыке, так как затяжка болта не контролируется. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.
где 
Проектировочный расчет.
Диаметр стержня из условия среза
Закон распределения напряжений смятия по цилиндрической поверхности контакта болта и детали трудно установить точно. Это зависит от точности размеров и форм деталей соединения. Поэтому расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений заменяют условной с равномерным распределением напряжений.
Для средней детали (и при соединении только двух деталей)
Формулы (23) и (24) справедливы для болта и деталей. Из двух значений [σ]см в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали. Сравнивая варианты постановки болтов с зазором и без зазора (рис.52 и 53), следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. Так, например, приняв коэффициент трения в стыке деталей f= 0,2, К = 1,5 и i = 1, из формулы (20) получим Fзаm = 7,5F. Следовательно, расчетная нагрузка болта с зазором в 7,5 раз превышает внешнюю нагрузку. Кроме того, вследствие нестабильности коэффициент трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна.
45. Расчёт на прочность стержня болта. Болты затянуты, внешняя нагрузка действует в плоскости стыка деталей (кронштейна).
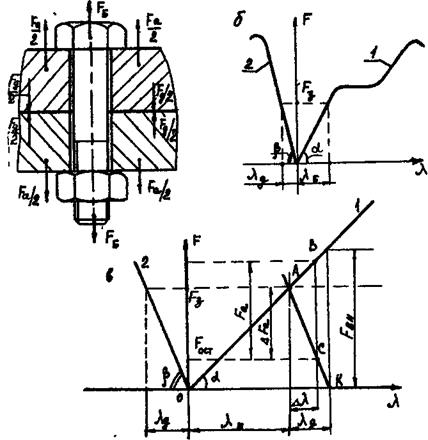
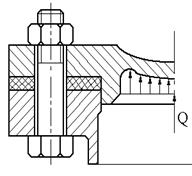
Этот случай является весьма распространенным (фланцевые, фундаментные и тому подобные болтовые соединения). Для большинства резьбовых изделий требуется предварительная затяжка болтов, обеспечивающая плотность и герметичность соединения и отсутствие взаимных смещений деталей стыка. После предварительной затяжки под действием силы предварительной затяжки болт растягивается, а детали стыка сжимаются. Помимо силы предварительной затяжки на болт может действовать внешняя осевая сила, которая создается за счет давления Q. Расчет ведут по результирующей нагрузке болта.
1)Внешние нагрузки передаются с одной детали на другую локально, через зоны, расположенные вокруг болтов.
2) Болт и детали испытывают упругие деформации, и это учитывается в расчетах.
3) Расчет ведут на предотвращение раскрытия стыка, то есть условие, при котором напряжения в стыке всегда сжимающие и не равны нулю.
4) Затяжку болтов ведут в условиях отсутствия внешней отрывающей силы.
5) Основной критерий расчета болта – условие нераскрытия стыка.
6) Условие нераскрытия стыка в инженерном расчете учитывается расчетом необходимой силы предварительной затяжки болта. Здесь термин «предварительная затяжка» означает, что затяжку ведут до приложения внешней силы, т.е. сборке.
Считаем, что усилие Qраспределяется между болтами фланца равномерно. Введем обозначения Fвн= 
По условию нераскрытия стыка: k=1,25÷2 – при постоянной нагрузке;
k=2,5÷4 – при переменной нагрузке.
По условию герметичности в стыке: k=1,3÷2,5 — при мягкой прокладке;
k=2÷3,5 – при фасонной металлической;
k=3÷5 – при плоской металлической прокладке.
Следовательно, растягивающая сила Fδ, действующая на болт, после предварительной затяжки и приложения внешней силы Fвн равна
При отсутствии последующей затяжки болт рассчитывают с учетом его кручения от момента трения в резьбе Тр по расчетной силе Fp =1,3Fзат+ xFвн
При отсутствии упругих прокладок коэффициент внешней нагрузки х=0,2÷0,3. При наличии упругих прокладок х может быть близок к единице.
Дополнительные условия повышения герметичности стыка:
1. Высокая чистота (малая шероховатость) соединенных поверхностей, т.к. шероховатости поверхности в процессе работы сминаются и остаточная затяжка стыка уменьшается. Для ответственных соединений поверхности стыков деталей рекомендуют шлифовать;
2. Чем меньше число стыков, тем больше гарантирована остаточная затяжка;
3. Высокая чистота обработки поверхности резьбы болта для уменьшения смятия шероховатостей и ослабления остаточной затяжки;
4. Контровка резьбового соединения;
5. Повышение упругости прокладок. Пружинные шайбы играют роль упругих прокладок. Необходимо помнить, что наличие прокладок увеличивает коэффициент основной нагрузки.
Источник
Напряженное состояние затянутого резьбового соединения.
При затяжке болтового соединения ключом детали сжимаются между гайкой, навинчиваемой на резьбовой колец болтали головкой болта (см. рисунок 73, а). Болт оказывается растянутым такой же силой, с которой сжимаются детали. При дальнейшей затяжке гайки стержень болта испытывает еще и напряжения кручения. Для большинства болтов момент, скручивающий его стержень, равен моменту в резьбе Тр, так как момент трения на торце гайки или головке болта через его стержень не передается. Таким образом, в стержне болта возникает сложное напряженное состояние — напряжение растяжения и кручения. Эквивалентное напряжение определяют по зависимости:
 |
Если вынести множитель sр = 4F/ (p × d1 2 ) за знак корня, то получим:
Для стандартных винтов с нормальной метрической резьбой, для которой Y = 2 0 30’, d2 = 1.12 × d1, f = 0.15, и b’ = 8 0 40’, [11,с.82], получим:
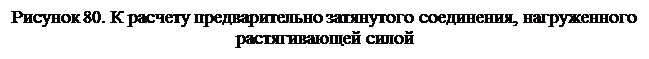
Дата добавления: 2015-02-19 ; просмотров: 1622 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
ИСПЫТАНИЕ ЗАТЯНУТОГО БОЛТОВОГО СОЕДИНЕНИЯ,
РАБОТАЩЕГО НА СДВИГ
Работа предназначается для определения сдвигающей силы F (расчетным и экспериментальным путем) в зависимости от момента затяжки болта Tзаm.
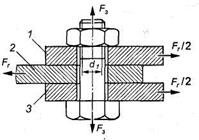
В испытуемом соединении (рис. 1) болт 1 поставлен с зазором, его стержень при затяжке (моментом на ключе Tзаm) растягивается и скручивается.
Пластины 2, 3 удерживаются от сдвига силами трения Fί, возникающими на поверхностях контакта. Условие, при котором начинается сдвиг, выражается зависимостью [1, c. 111–113; 2, с. 36–37; 3, с. 95–96].
где F – предельная сдвигающая сила; n – число поверхностей трения.
где F0 – усилие предварительной затяжки; fc – коэффициент трения на стыке. Таким образом,
Если коэффициент трения на стыке принять постоянным (при изменении усилия затяжки), то зависимость силы сдвига от величины F0 будет линейной.
Момент на ключе и сила затяжки связаны между собой формулой [1, c. 105–107; 2, c. 28–30; 3, c. 83–85].

где Tp – момент трения в резьбе; Tт – момент трения на торце гайки; d2 – сред-ний диаметр резьбы; ψ – угол подъема резьбы; φ – приведенный угол трения в резьбе; fт – коэффициент трения на торце гайки; H – размер под ключ; d0 – внутренний диаметр опорной поверхности гайки (диаметр отверстия под болт).
Определив из формулы (4) F0 и подставив его выражение в основное условие (3), получим
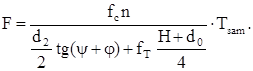

где 
где fp – коэффициент трения в резьбе; β – угол наклона рабочей стороны профиля резьбы к плоскости поперечного сечения (для метрической резьбы β = Исследуемый узел «Болт-пластины», динамометрический ключ со сменной головкой, штангенциркуль, резьбомер. 4. Порядок выполнения работы Пластины 1 (рис. 2), болт 2 с шайбой 3 и гайкой 4 выбираются по указа-нию преподавателя. Расчет силы трения при сдвиге. Замеряются: наружный диаметр резьбы болта (d); шаг резьбы (Р); размер под ключ (H); диаметр отверстия под болт (dо) и округляются до ближайших значений по ГОСТ. Внутренний диаметр (d1) и средний (d2) берутся из таблиц ГОСТа, а угол ψ определяется по формуле (6). Расчетная сила F определяется по формуле (3), причем в качестве силы прижатия пластин (F0) следует брать силу, не превышающую допускаемую ([F0]) из условия прочности болта на растяжение. Коэффициенты трения скольжения на поверхностях стыка пластин (fc), торце гайки (fт) и в резьбе (fр) ориентировочно можно выбирать из табл. 1.
|









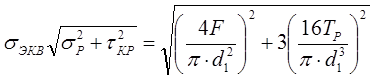

 /6, cos
/6, cos 
 .
. ?
?