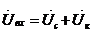Порядок выполнения работы.
Лабораторная работа № 12.
Тема: «Исследование резонанса напряжений в электрических цепях».
Цель: Исследование резонанса напряжений: снять резонансные кривые при переменной ёмкости, определить на опыте соотношения между сопротивлениями отдельных участков и падениями напряжения на них, между активными и реактивными мощностями. Снять резонансные кривые при переменной ёмкости.
Резонансом напряжений называют такой режим работы неразветвлённой электрической цепи, содержащий участки с индуктивностью и ёмкостью, при котором разность фаз напряжения на зажимах цепи и тока на входе цепи равна нулю. При этом сопротивления на реактивных участках равны между собой: 2πfL=1/2πfC=Zв,
где Zв= 
Резонанс можно получить изменением частоты, индуктивности или ёмкости. При резонансе напряжений сила тока в цепи максимальная, что позволяет на опыте фиксировать точку резонанса по показаниям амперметра. Падения напряжения на реактивных участках равны между собой: UL=I*XL=I*XC=UC, кроме того UL=U(XL / R) и UC=U(XC /R), т.е. они будут больше напряжения на зажимах цепи, если XL=XC>R.
Векторы напряжений UL и UC сдвинуты относительно друг друга на угол 180 0 , поэтому взаимно компенсируются при сложении: U= 
Полная мощность будет иметь активный характер: S=U*I= 
Форма резонансных кривых в значительной степени зависит от соотношения активного и волнового сопротивлений в цепи. Это соотношение учитывается добротностью контура: Q = 

Чем больше добротность, тем более острую форму будут иметь кривые тока, напряжений и мощностей.
Из анализа этой формулы следует, что резонанса можно добиться, изменяя частоту генератора, индуктивность катушки, ёмкость конденсатора или активные сопротивления. При резонансе токов: BL=BC; IL=IC; IL-IC=0; I=IQ1+IQ2, т.е. ток чисто активный и, следовательно, совпадает по фазе с напряжением на зажимах цепи (φ=0). Кроме того, он минимален, так как отсутствуют реактивные токи.
Если BL>G1, a BC>G2, то IL>IQ1 и XC>IQ2, тогда возможен случай, при котором: I1>I=IQ1+IQ2, I2>I, т.е. сила токов в отдельных ветвях может оказаться больше, чем сила тока на входе цепи.
Активная мощность в ветвях: P1=IQ1*U= 
P2=IQ2*U= 
S= 
т.е. полная мощность цепи равна активной. Это означает, что генератор снабжает цепь энергией, превращающейся в теплоту в активном сопротивлении катушки и конденсатора.
Добротность контура Q=IL / I=IC / I=YB / Q , где YB=BL=BC – волновая проводимость цепи; IL и IC – реактивные токи при резонансе. Чем меньше активные сопротивление цепи, тем меньше потери энергии в ней и тем больше добротность контура.
Порядок выполнения работы.
1. Ознакомится с приборами, необходимыми для работы. Собрать схему согласно рисунку 1показать её преподавателю и объяснить принцип и особенности работы.
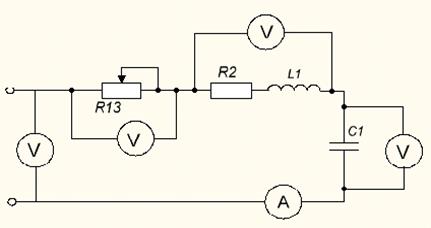 |
2. Установить в цепи по максимуму тока резонансный режим работы. Изменением величины ёмкости конденсатора добиться равенства индуктивного и ёмкостного сопротивлений.
3. Вычислить значение индуктивности катушки по результатам опыта, приняв Rк=18 Ом.
4. Измерить напряжение на элементах схемы и ток в цепи. Значения записать в таблицу 1.
5. Установить значение ёмкости больше, чем С0, затем меньше С0, снять значение напряжений на элементах цепи и записать их в таблицу 1.
6. Построить по результатам опыта векторные диаграммы для всех трёх режимов работы электрической цепи.
7. Определить кратность превышения индуктивного или ёмкостного напряжения над напряжением на входе цепи при резонансе, т.е. добротность: Q= 

| С, мкФ | I, A | UR, В | UL, В | UC, В | U, В |
| Измерение | |||||
| Измерение Расчёт | |||||
| Измерение |
8. Рассчитать частотные характеристики и изобразить их графики: XL=f(ω), XL=f(ω),
Z=f(ω), I=f(ω), φ=f(ω). Результаты расчёта занести в таблицу 2.
| ω, С -1 |
| XL, Ом |
| XC, Ом |
| Z, Ом |
| I, A |
| φ, 0 |
9. Определить полосу пропускания контура, проведя линию на высоте отношения I / / I0=1 / 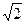
L= 

P=U*I*cosφ; Z= 


P=U*I*cosφ; S= 
10. Сделать заключение относительно:
а) возможности получения резонанса путём изменения ёмкости цепи;
б) характера изменения резонансных кривых. Выводы записать в отчёт.
1. Что называют резонансом напряжений?
2. Каким образом можно достичь резонанса напряжений?
3. Каковы характерные особенности сопротивлений цепи при резонансе напряжений?
4. Какую величину имеет коэффициент мощности и угол φ при резонансе напряжений?
5. Каким образом можно определить на опыте состояние резонанса напряжений?
6. Каковы особенности падений напряжений на отдельных участках исследуемой цепи при резонансе напряжений?
7. Что называют добротностью контура?
8. Что называют резонансом токов?
9. Каким образом можно достичь резонанса токов?
10. Каковы характерные особенности проводимости цепи при резонансе токов?
11. Каким образом можно определить на опыте и зафиксировать резонанс токов?
12. Какова особенность токов в ветвях при резонансе токов?
Источник
Исследование резонанса напряжений
Цель работы
Исследовать электрическую цепь с последовательно соединенными активным сопротивлением, конденсатором и катушкой с регулируемой индуктивностью. Выяснить условия возникновения резонанса напряжений.
Теоретические сведения
В неразветвленной электрической цепи (рисунок 2.1) при прохождении гармонического тока i = Im sinωt на зажимах создается гармоническое напряжение, равное алгебраической сумме мгновенных значений напряжений на отдельных элементах (второй закон Кирхгофа):
Рисунок 2.1 Неразветвленная электрическая цепь
На рисунке 2.2,а показаны кривые тока и напряжения, при этом напряжение на активном сопротивлении (uR) совпадает по фазе с током, на индуктивном элементе напряжение (uL) опережает ток на угол π/2, а на емкостном элементе напряжение (uC) отстает от тока на угол π/2.
Рисунок 2.2 Напряжение на активном, индуктивном, емкостном
сопротивлении при гармоническом токе:
а) кривые напряжений; б) векторная диаграмма
Построение векторной диаграммы (рисунок 2.2, б) осуществляется с учетом известных фазовых соотношений. Вектор напряжения на резисторе совпадает по фазе с вектором тока, на конденсаторе он отстает от вектора тока на 90°, а на катушке опережает вектор тока на 90°. Сумма этих векторов напряжений на элементах цепи, даст вектор напряжения источника. Из векторной диаграммы определяем напряжение на зажимах всей цепи:
U = 
где UR = IR – активная составляющая напряжения,
UL = IXL – индуктивная составляющая напряжения,
UС = IXС – емкостная составляющая напряжения.
Полное сопротивление цепи найдем из закона Ома, либо из треугольника сопротивлений (рисунок 2.3):
z = 
z = 
где Х = XL — XС – реактивная составляющая сопротивления;
XL = ω L – индуктивная составляющая реактивного сопротивления;
XС = 
ω = 2πf – угловая частота (f = 50 Гц).
Рисунок 2.3 Треугольник сопротивлений
Сдвиг фаз определяется из треугольника напряжений или сопротивлений:
φ = arctg 

В зависимости от знака величины (ХL – XC) сдвиг фаз может быть либо положительным (φ > 0 – индуктивный характер цепи), либо отрицательным (φ
В установке использован осциллограф для визуального наблюдения за опережением или отставанием напряжения от тока по фазе на угол jв зависимости от соотношения между напряжениями UL и UC. Для одновременного наблюдения на экране осциллографа двух процессов в нем имеется электронный коммутатор. Клеммы коммутатора расположены с левой стороны осциллографа («Вход 1», «Вход 2»). Ручками «Усиление 1» и «Усиление 2» устанавливают требуемую величину амплитуд исследуемых сигналов. Смещение осциллограмм по вертикали относительно друг друга осуществляют ручкой «Смещение».
2.4.2 Собрать электрическую схему установки (рисунок 2.4), уяснить назначение отдельных ее элементов и дать проверить ее преподавателю.
2.4.3 Перед подачей напряжения к установке рукоятку ползунка Т1 устанавливают на «0». На экране осциллографа будут две горизонтальные линии, которые совмещают в одну, пользуясь ручкой «Смещение». С помощью ЛАТРа устанавливают напряжение 30 или 60 В (по указанию преподавателя). Величину этого напряжения сохранять неизменной.
2.4.4 Изменяя индуктивное сопротивление цепи, при различных значениях 
Таблица 2.2 Параметры электрической цепи при различных видах нагрузки
Источник
Исследование резонанса напряжений
Цель работы: Изучение и экспериментальное исследование явления резонанса напряжений.
Основные теоретические сведения
Резонансом называется такой режим электрической цепи, при которой входной ток совпадает по фазе с входным напряжением, несмотря на наличие в цепи реактивных элементов.
Резонансный режим наступает тогда, когда частота внешних воздействий на систему равна собственной частоте системы,
т.е. частоте преобразования энергии внутри системы из одной формы в другую (энергия магнитного поля в энергию электрического поля и наоборот). Резонанс, таким образом, возникает при наличии в цепи индуктивности и емкости.
Одна из ценных особенностей резонансов — это значительное увеличение напряжений или токов при весьма экономичном использовании электрической энергии.
Резонанса в электрической цепи можно достичь, изменяя либо частоту источника питания, либо индуктивность, либо емкость.
Цепь, находящаяся в резонансном режиме, характеризуется следующим:
1. входные реактивные сопротивления или проводимости равны нулю:
xвх=0; 
2. угол сдвига фаз между входным током и выходным напряжением равен нулю, а коэффициент мощности максимален.
3. входная мощность чисто активная:
Резонанс напряжений
Резонанс при последовательном соединении индуктивности и емкости, при взаимной компенсации реактивных составляющих напряжения Uвх, называют резонансом напряжений.
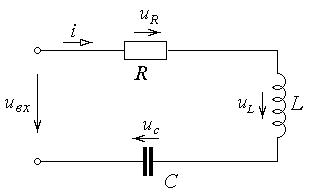
Если к цепи, изображенной на рис. 4-1, приложено переменное синусоидальное напряжение


Из приведенного выражения (4.3) видно, что ток iвх будет совпадать с приложенным напряжением при условии xвх = 0 или
Таким образом, при резонансе напряжений входное реактивное сопротивление xвх равно нулю, а полное сопротивление zвх имеет наименьшее значение, поэтому ток в цепи максимален.
При резонансе напряжений реактивные составляющие напряжения Uвх равны между собой:
и могут во много раз превышать напряжение, приложенное к цепи, что характеризуется добротностью контура:
где ρ — волновое или характеристическое сопротивление контура.

Рис. 4-1. Схема замещения последовательной цепи
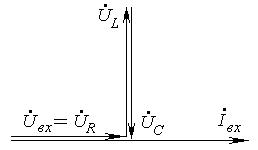
Векторная диаграмма резонанса напряжений в цепи (рис. 4-1) имеет вид:
Рис. 4-2. Векторная диаграмма резонанса напряжений
Нерезонансные режимы
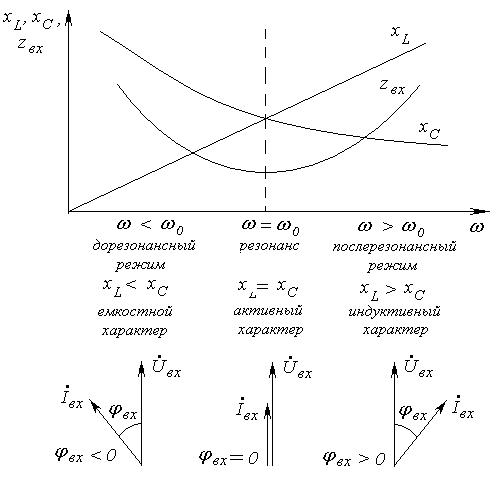
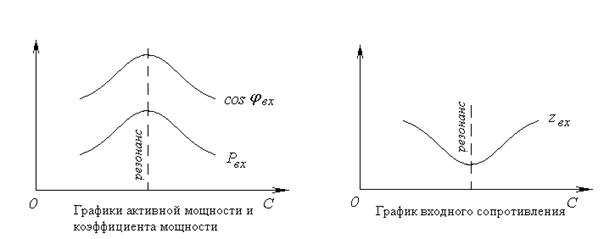
Режимы вне резонанса можно получить, если вывести систему из резонанса, т.е. нарушить условие (4.1), изменяя собственную частоту контура с помощью индуктивности L при постоянной емкости C, или изменяя емкость C при постоянной индуктивности L. В результате этой операции можно получить частотные характеристики (рис. 4-3 и рис. 4-4).
Следует отметить, что острота всех частотных характеристик зависят от добротности цепи Qg. Чем выше Qg, тем более острыми получаются пики всех кривых и поэтому резко возрастают избирательные свойства цепи.
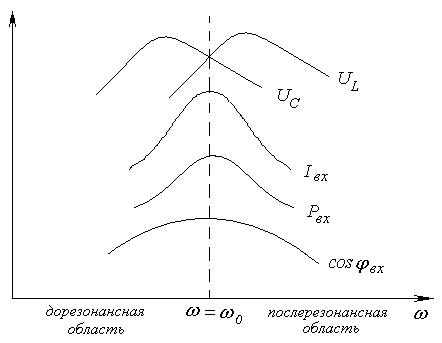
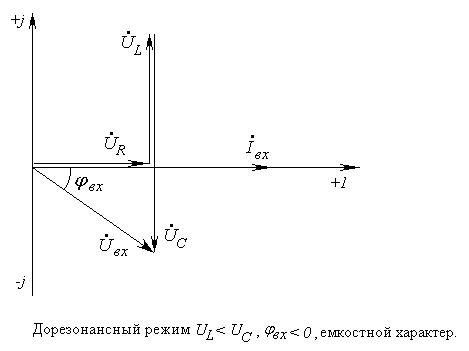
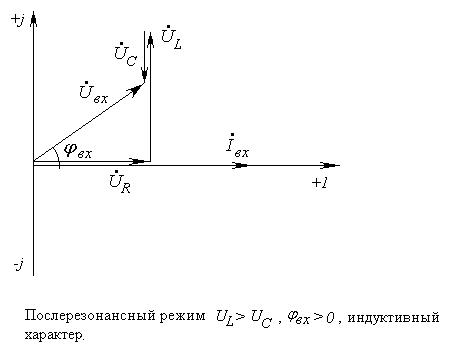
Изменяя величину емкости конденсатора при постоянной индуктивности можно получить графики функциональных зависимостей в последовательной цепи (рис. 4-5) и построить соответствующие векторные диаграммы (рис. 4-6).
Для схемы (рис. 4-1) на основании векторных диаграмм для нерезонансных режимов (рис. 4-6) можно построить треугольник напряжений для всей цепи (рис. 4-7, a) и соответствующий треугольник сопротивлений (рис. 4-7. б).
Из треугольника напряжений (рис. 4-7,а) следует:
где Ua— активная составляющая входного напряжения.
Из треугольника сопротивлений также можно определить величину коэффициента мощности:
Рис. 4-3. Частотные характеристики сопротивлений последовательной цепи
Рис. 4-4. Частотные характеристики тока, напряжения, мощности и коэффициента мощности последовательной цепи
Рис. 4-5. График функциональных зависимостей в последовательной цепи
Рис. 4-6. Векторные диаграммы последовательной цепи для нерезонансных режимов
Рис. 4-7. Треугольник напряжений (а) и треугольник сопротивлений (б) последовательной цепи
Перечень оборудования
1. Источники переменного напряжения 36 В, 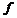
2. Катушка индуктивности с ферромагнитным сердечником с подмагничиванием (подмагничивание постоянным током уменьшает эквивалентную индуктивность катушка). Цепь подмагничивания включается тумблерами.
3. Батарея конденсаторов со ступенчатым регулированием 94 мкФ.
4. Амперметр с пределом измерений 2А.
5. Вольтметры — 3 шт. с пределами измерений 250 В, 100 В.
Содержание работы
Исследовать дорезонансный, резонансный и послерезонансный режимы последовательной цепи изменением индуктивности при постоянной емкости и изменением емкости при постоянной индуктивности. Измерить параметры катушки при помощи амперметра, вольтметра и ваттметра.
Порядок выполнения работы
1. Собрать схему для исследования последовательной цепи (рис. 4-8).
Рис. 4-8. Схема исследования последовательной цепи
2. Ключ В1 разомкнут. Включаем выключатели батареи конденсаторов, набираем суммарную емкость 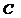
3. Изменяя, индуктивность катушки, установить дорезонансный режим (ток в цепи увеличивается), затем — послерезонансный режим (ток в цепи уменьшается). Показания приборов для одной точки дорезонансного режима и одной точки послерезонансного режима занести в табл. 4-1.
 , В
, В , А
, А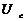 , В
, В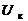 , В
, В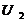 , В
, В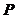 , Вт
, Вт4. По данным табл. 4-1 построить векторные диаграммы цепи для трех режимов: резонансного, дорезонансного и послерезонансного. Диаграмму удобно строить методом засечек с помощью циркуля, в соответствии с балансом напряжений.
5. Установить ток Iвх=0,5 А. регулированием индуктивности. Выключить батарею конденсаторов с помощью тумблеров, замкнуть ключ В1. Показания приборов занести в табл. 4-2
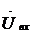 , В
, В , А
, А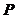 , Вт
, Вт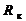 , Ом
, Ом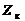 , Ом
, Ом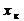 , Ом
, Ом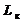 , Гн
, Гн 

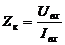
7. Разомкнуть ключ В1. Включить суммарную емкость 30 мкФ. Изменяя индуктивность, установить резонансный режим. Оставив индуктивность неизменной, записать показания приборов при ступенчатом изменении емкости в пределах имеющегося магазина емкостей. Показания приборов занести в табл. 4-3.
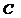 , мкФ
, мкФ  , В
, В , А
, А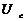 , В
, В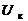 , В
, В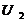 , В
, В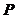 , Вт
, Вт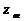 , Ом
, Ом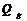
8. По данным табл. 4-3 построить графики зависимостей:
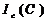

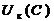
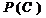
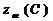
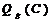
cos φвх(С) — определяется из соотношения (4.8)
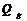
Содержание отчета
4. Таблицу приборов и оборудования.
5. Таблицы с результатами измерений и вычислений.
9. Выводы об особенностях резонансного и нерезонансного режимов.
Контрольные вопросы
1. Что такое резонанс напряжений?
2. Каким способом регулируется собственная частота цепи?
3. Чем определяется величина усиления напряжений?
4. Почему выходной ток при резонансе напряжений максимален?
5. Почему коэффициент мощности при резонансе равен единице, а до и после резонанса снижается?
6. Как строятся векторные диаграммы для нерезонансных режимов?
7. Почему резонансные режимы весьма экономичны?
8. Где используется резонансы напряжений?
1. Электротехника [Текст]: / Под ред. В. С. Пантюшина.- М.: Высшая школа , 1976. — гл.5, С.108 — 111.
2. Касаткин, А.С. Электротехника [Текст]: / А.С. Касаткин, М.В. Немцов; — М.: Высшая школа, 2002. — гл.12, с. 339-356.
3. Бессонов, Л.А. Теоретические основы электротехники. [Текст]: — М.: Гардарики, 2001. — §1.28.
Источник