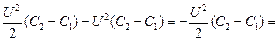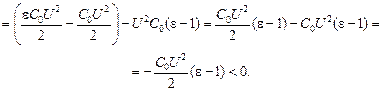Раздвижение пластин конденсатора
Задача 4.2. Изолированный воздушный конденсатор заряжен зарядом Q, площадь его пластин S, а расстояние между пластинами d1. Какую работу необходимо совершить внешней силой, чтобы увеличить расстояние между пластинами до величины d2 > d1?
| Q S d1 d2 d2 > d1 | Решение. Работа внешней силы пойдет на увеличение энергии конденсатора, поэтому А = W2 – W1 = 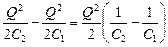 = = 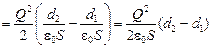 . . |
| А = ? |
Ответ: А 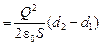
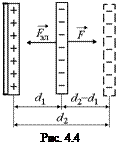
Автор: Можно. Ведь чтобы раздвинуть пластины, одну из них надо закрепить, а к другой приложить силу, равную той, с которой притягиваются пластины, и переместить незакрепленную пластину на расстояние (d2 – d1) (рис. 4.4). Сила F с которой притягиваются пластины, равна
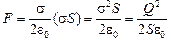
А = F(d2 – d1) = 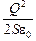
Как видим, мы получили тот же результат.
СТОП! Решите самостоятельно: А6, В3–В5.
Задача 4.3. Плоский воздушный конденсатор подключили к источнику постоянного напряжения величины U. Площадь пластин конденсатора S, расстояние между ними d1. Какую работу необходимо совершить внешней силой, чтобы уменьшить расстояние между пластинами до величины d2 0, т.е. Авнеш > 0! А Вы только что доказали, что Авнеш С1. Следовательно, заряд на пластинах также увеличивается:
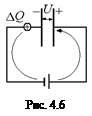
Таким образом, источник напряжения как бы «перетащил» заряд DQ = Q2 – Q1 = (C2 – C1)U с отрицательно заряженной пластины на положительно заряженную (рис. 4.6). При этом источнику пришлось совершить работу против сил электрического поля в конденсаторе:
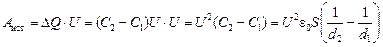
А общая работа источника напряжения и внешней силы как раз равна изменению энергии конденсатора:
Авнеш = (W2 – W1) – Аист = =
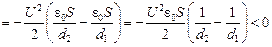
Как видите, работа внешних сил действительно получилась отрицательной.
Ответ: 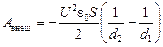
Читатель: Если пластины раздвигать, то работа внешних сил, конечно, будет положительной, а вот какой будет работа источника?
Автор: Отрицательной. Ведь заряды на пластинах будут уменьшаться, следовательно, DQ = Q2 – Q1
Задача 4.4. Изолированный конденсатор имеет заряд Q. Между его обкладками находится пластина из диэлектрика с диэлектрической проницаемостью e. Емкость конденсатора без пластины равна С. Какую работу надо совершить внешней силой, чтобы вытащить пластину из конденсатора?
| Q С e | Решение. Читатель: Я не понимаю, почему для того, чтобы вытащить пластину диэлектрика из конденсатора, надо совершать работу. Ведь поле в конденсаторе однородно, значит, никаких сил, действующих по касательным к пластинам, быть не может. Кроме того, пластина из диэлектрика электрически нейтральна. Автор: Во-первых, на краях обкладок поле неоднородно, а во-вторых, не надо забывать про поляризационные заряды! Силовые линии на краях конденсатора имеют вид, показанный на рис. 4.7. Мы видим, что |
| Авнеш = ? | |
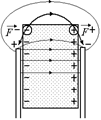 Рис. 4.7 Рис. 4.7 |
напряженность поля там как раз имеет касательную к пластинам составляющую. И именно из-за этого на поляризационные заряды действует сила, «возвращающая» пластину в конденсатор. Поэтому чтобы вытащить пластину из конденсатора, необходимо приложить внешнюю силу.
Теперь осталось вычислить работу внешней силы. Если емкость конденсатора без диэлектрика равна C0, то емкость с диэлектриком eС0. Тогда начальная энергия конденсатора 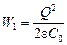
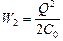
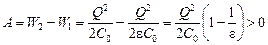
Ответ: 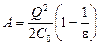
СТОП! Решите самостоятельно: А7, В7–В9, С7.
Задача 4.5. Воздушный конденсатор емкостью С0 подключен к источнику напряжения U. Какую работу надо совершить внешней силе, чтобы вставить в конденсатор пластину из диэлектрика с диэлектрической проницаемостью e?
| U C0 e | Решение. Сначала заряд на конденсаторе был равен Q1 = C0U. После того как вставили пластину, заряд увеличился и стал равным Q1 = eC0U. Следовательно, источник совершил работу Аист = U(Q2 – Q1) = U(eC0U – C0U) = U 2 C0(e – 1) > 0. |
| Авнеш = ? |
Суммарная работа источника и внешней силы равна изменению энергии конденсатора:
Авнеш = (W2 – W1) – Аист =
Таким образом, работа внешней силы отрицательна: пластина сама будет втягиваться в конденсатор.
Ответ: Авнеш 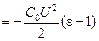
СТОП! Решите самостоятельно: В11, В12, В14.
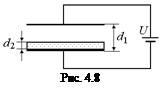
| U S d1 d2 m | Решение. Если бы конденсатор не был подключен к источнику напряжения, то после того, как пластинка «подпрыгнула» и ударилась о верхнюю обкладку, конденсатор бы полностью разрядился. Однако в данном случае источник «загонит» на обкладку новые заряды +q и –q в точности равные старым: q = CU. При этом |
| υ = ? |
энергия конденсатора 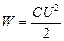
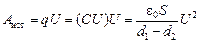
И эта работа как раз и пойдет на увеличение кинетической энергии пластинки: 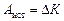
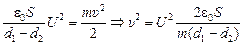
Ответ: 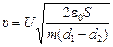
Источник
конденсаторы — Раздвижение/сближение пластин конденсатора.
Пусть дан конденсатор в цепи с батареей(ЭДС). Пусть конденсатор зарядился до ЭДС. При раздвижении пластин конд.(в заряженном состоянии) мы совершаем работу, куда девается это работа, переходит в энергию конденсатора?
задан 25 Янв ’14 20:29
Dragon65
328 ● 9 ● 27
86% принятых
1)Конденсатор зарядился до напряжения или разности потенциалов, но не до ЭДС. 2)Работа не девается, она лишь производится за счет трансформации энергии. Поскольку напряжение на конденсаторе остается постоянным, его энергия W = CU^2 / 2 убывает, так как при раздвижении пластин уменьшается емкость конденсатора. Если рассмотреть всю систему источника тока — конденсатор, то видно, что заряд от конденсатора перетекает к источнику тока. Часть энергии, запасенной в конденсаторе, может при этом расходоваться на нагревание соединительных проводников, часть может перейти в источник тока.
1 ответ
При раздвижении обкладок внешняя сила совершает работу, что приводит к изменению энергии конденсатора. При этом возможны два случая: когда конденсатор заряжен и отключен от источника тока и когда он подключен к нему постоянно. Во втором случае нужно еще учитывать работу сторонних сил в источнике. Работа, необходимая для того, чтобы раздвинуть пластины на одинаковое расстояние, в обоих случаях будет одинаковая, а энергия конденсатора в первом случае увеличится, а во втором — уменьшится.
отвечен 25 Янв ’14 22:22
Из-за чего при раздвижении пластин отключенного от ЭДС и заряженного конденсатора его энергия увеличится?
Из-за того, что раздвигая пластины Вы совершаете над конденсатором механическую работу. A = ΔW = q^2/C2 — q^2/C1 > 0, поскольку C2 (26 Янв ’14 10:16) zolton
И получается моя работа идет «В» конденсатор в этом случае?) НО я то работаю внешне, а там электрическое поле, оно просто в объеме увеличивается,такой переход E?
Если над телом совершают работу, то его энергия увеличивается, если само тело совершает работу — энергия уменьшается. Энергия конденсатора — это энергия электростатического поля между обкладками. Если конденсатор заряжен и отключен от источника, то при раздвижении обкладок его энергия увеличивается: напряженность поля между обкладками в этом случае не изменяется (не изменяется плотность энергии электростатического поля), а объем увеличивается, следовательно энергия увеличивается. Если конденсатор подключен к источнику, то меняется заряд на обкладках, следовательно меняется напряженность поля.
Источник
Найти энергию конденсатора до и после раздвижения пластин
Определить энергию поля конденсатора и силу взаимного притяжения пластин.
Расстояние между пластинами плоского конденсатора d=2мм, разность потенциалов u=600 В. Заряд.
Найти заряд, перетекший с пластин первого конденсатора на второй
Конденсатор электроемкостью С= 0,6 мкФ был заряжен до разности потенциалов U1=300В и соединен.

Найдите энергию конденсатора, заряженного до разности потенциалов U=50 B, если площадь пластин.
Найти энергию конденсатора в магнитном поле
Пожалуйста помогите решить задачу. проводящий контур площадью S = 400 см2, в который включен.
1)
e0 — электрическая постоянная 8,854 *10^-12 Ф/м
S — площадь пластин
d — расстояние между пластинами
Добавлено через 49 секунд
Энергия заряженного конденсатора
W = C*U^2/2
где U — напряжение на обкладках конденсатора
Добавлено через 5 минут
Ёмкость конденсатора до раздвигания пластин
C1 = e0*S/d1 = 8,854 *10^-12*(100*10^-4)/10^-3 = 88,54*10^-12 Ф
Ёмкость конденсатора после раздвигания пластин
C2 = e0*S/d1 = 8,854 *10^-12*(100*10^-4)/(25*10^-3) = 3,54*10^-12 Ф
Добавлено через 3 минуты
Энергия конденсатора до раздвигания пластин
W1 = C1*U^2/2 = 88,54*10^-12*(100)^2/2 = 44,27*10^-8 Дж
Энергия конденсатора после раздвигания пластин
W2 = C2*U^2/2 = 3,54*10^-12*(100)^2/2 = 1,77*10^-8 Дж
Источник
Материалы для практических занятий по общей физике (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 |
5. При последовательном соединении конденсаторов:
q1= q 2= . = q n= q 0; 
6. При параллельном соединении конденсаторов:
C0=C1+C2+. +Cn=
7. Энергия поля заряженного конденсатора:
W=
Задача 1. Три заряженные водяные капли радиусом 1 мм каждая сливаются в одну большую каплю. Найти потенциал большой капли, если заряд малой 10-10 Кл.
Решение. Потенциал большой капли j=Q/C, где Q — заряд большой капли. Радиус R большой капли найдем из закона сохранения массы: M=nm, где М =r(4/3)pR3, а m=r(4/3)pr3. Тогда R3=n r3. R = r n1/3. Отсюда: 
Задача 2. Расстояние между пластинами плоского воздушного конденсатора, присоединенного к источнику напряжения с ЭДС 180 В равно 5 мм. Площадь пластин конденсатора 175 см2. Найти работу по раздвижению пластин до расстояния 12 мм, если конденсатор перед раздвижением пластин отключен от источника.
Дано: e =180 В, d1 =5.10-3 м, d2 =12.10-3 м, S = 1,75.10-2 м2.
Решение. При раздвижении пластин меняется емкость конденсатора, а заряд на пластинах остается постоянным, так как конденсатор отключен от источника. Следовательно, меняется энергия заряженного конденсатора. Работа по раздвижению пластин равна изменению энергии конденсатора, т. е. А=DW=W2 — W1 , (1)
Емкость конденсатора до раздвижения пластин 

Заряд на пластинах найдем из условия q=C1U1 = e0Se / d1, так как U1=e. Таким образом, А =e0Se 2 (d2 — d1)/(2 d12)
Задача 3. Пластины плоского конденсатора подключены к источнику с E = 2 B. Определите изменение емкости и энергии электрического поля конденсатора, если конденсатор наполовину заполнен диэлектриком с диэлектрической проницаемостью e=2. Расстояние между пластинами d=1 см, площадь пластин S=50 см2.
Решение. Такой конденсатор, наполовину заполненный диэлектриком можно представить как два параллельно соединенных конденсатора с площадью пластин S’ = S/2, один из которых заполнен диэлектриком. Тогда С1=e0S’/d=e0S/2d — емкость первого, воздушного, конденсатора, а С2=ee0S/2d -емкость второго, заполненного диэлектриком. Общая емкость
Первоначальная емкость С0=e0S/d.
DС = С — С0 = (e+1)e0S/2d — e0S/d = (e — 1) e0S/2d,
Изменение энергии конденсатора DW = C e2/2 — C0e2/2 = DС e2/2,
После вычислений получим: DС =2,21.10-12 Ф. DW =4,42.10-12Дж.
Задача 4. В плоский воздушный конденсатор вставляется металлическая пластина толщиной d0. Заряд на обкладках конденсатора q. Конденсатор отключен от источника. Расстояние между пластинами d, площадь пластин S. Определить изменение емкости конденсатора и энергии электрического поля.
Решение. На металлической пластине индуцируется заряд, причем внутри пластины поле равно нулю. Конденсатор с вставленной пластиной можно представить как два последовательно соединенных конденсатора с емкостями: С1=e0S/l1 и С2=e0S/l2, где l1 и l2 — расстояния от обкладок до металлической пластины (рис. б). Суммарная емкость равна:
Так как l1 + l2= d –d0, то С= e0S/(d — d0).
Изменение электроемкости равно:

то есть емкость конденсатора увеличивается, причем не зависит от локализации пластины.
Изменение энергии электрического поля DW= W1 — W2:
DW=
Энергия электрического поля уменьшилась, так как уменьшается объем, в котором создается поле, напряженность же поля в пространстве между пластинами остается прежней.
Задачи для самостоятельного решения.
4.1. Найти емкость земного шара. Считать радиус земного шара 6400 км. На сколько изменится потенциал земного шара, если ему сообщить заряд 1 Кл?
4.2. Восемь заряженных водяных капель радиусом 1 мм и зарядом 0,1 нКл каждая сливаются в одну общую водяную каплю. Найти потенциал большой капли.
4.3. Требуется изготовить конденсатор емкостью С=250 пФ. Для этого на парафинированную бумагу толщиной d=0,05 мм наклеивают с обеих сторон кружки станиоля. Каким должен быть диаметр D кружков станиоля?
4.4. Площадь пластин плоского воздушного конденсатора 0,01м2, расстояние между ними 5 мм. К пластинам приложена разность потенциалов U1=300 В. После отключения конденсатора от источника напряжения пространство между пластинами заполняется эбонитом. Какова будет разность потенциалов между пластинами после заполнения? Найти емкость конденсатора С1 и С2 и поверхностные плотности заряда s1 и s2 на пластинах до и после заполнения.
4.5. Решить предыдущую задачу для случая, когда заполнение пространства между пластинами изолятором производится при включенном источнике напряжения.
4.6. Радиус центральной жилы коаксиального кабеля r=1,5 см, радиус оболочки R=3,5 см. Между центральной жилой и оболочкой приложена разность потенциалов U=2,3 кВ. Найти напряженность электрического поля на расстоянии x=2 см от оси кабеля.
4.7. Каким будет потенциал шара радиусом 3 см, если: а) сообщить ему заряд 1 нКл, б) окружить его концентрическим шаром радиусом 4 см, соединенным с землей?
4.8. Найти емкость сферического конденсатора, состоящего из двух концентрических сфер с радиусами 10 см и 10,5 см. Пространство между сферами заполнено маслом. Какой радиус должен иметь шар, помещенный в масло, чтобы иметь такую же емкость?
4.9. Найти емкость системы конденсаторов, изображенной на рисунке 4.9. Емкость каждого конденсатора 0,5 мкФ.
4.10 Разность потенциалов между точками А и В 6 В (см. рис.4.10). Емкость первого конденсатора 2 мкФ и емкость второго конденсатора 4 мкФ. Найти заряды q1 и q2 и разности потенциалов U1 и U2 на обкладках каждого конденсатора.
4.11. Шар радиусом 1 м заряжен до потенциала 30кВ. Найти энергию заряженного шара.
4.12 Шар, погруженный в керосин, имеет потенциал 4,5 кВ и поверхностную плотность заряда 11,3 мкКл/м2. Найти радиус, заряд, емкость и энергию шара.
4.13. Площадь пластин плоского воздушного конденсатора 0,01м2, расстояние между ними 2 см. К пластинам приложена разность потенциалов U1=3 кВ. Какова будет напряженность поля конденсатора, если, не отключая его от источника напряжения, пластины раздвинуть до расстояния 5 см? Найти энергии конденсатора до и после раздвижения пластин?
4.14 Решить предыдущую задачу при условии, что сначала конденсатор отключается от источника напряжения, а затем раздвигаются пластины конденсатора.
4.15 Два проводника имеют одинаковую форму и размеры, причем один из них полый, а другой сплошной. Если сообщить каждому из них одинаковый заряд, то будут ли потенциалы равны?
4.16 Заряженный медный и стальной шары одинакового радиуса приводят в соприкосновение. Как распределятся на них заряды?
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
5. Основные законы постоянного тока.
1. Сила постоянного тока I = q/t,
q — заряд, прошедший через поперечное сечение проводника за время t.
S — площадь поперечного сечения.
При равномерном движении заряженных частиц
где n — концентрация частиц, q — заряд одной частицы.
3. Закон Ома для участка цепи, не содержащем ЭДС
I =
где j1 — j2=U — разность потенциалов (напряжение на концах участка), R — сопротивление участка.
4. Сопротивление однородного проводника длиной l и площадью поперечного сечения S: R=
где r — удельное сопротивление вещества проводника.
Источник