НАПРЯЖЕНИЯ В ДВИЖУЩЕЙСЯ ВЯЗКОЙ ЖИДКОСТИ



Рассмотрим элементарный объем в виде параллелепипеда с ребрами dx,dy,dz, который выделим из движущейся жидкости (рис. 5.1).
Обозначим напряжения на гранях, ближайших к началу координат (АВКЕ, AEHD, ABCD), через рхх, руу, pzz, txy, txz, tyx, tyz, tzx, tzy.
Рис.5.1. Схема действия напряжений в движущейся
Первый индекс указывает ось, которой перпендикулярна данная грань, т.е. направление нормали к граням, второй — направление действия напряжения, т.е. параллельно какой оси координат оно направлено. Так, касательное напряжение tyx действует на грани, перпендикулярной оси OY, в направлении оси ОХ; tzx действует на грани, перпендикулярной оси OZ, в направлении оси ОХ и т.д.
Считая напряжения непрерывно изменяющимися по объему жидкости, получим значения напряжений на всех гранях параллелепипеда, пользуясь разложением функций напряжения в ряд Тейлора (табл. 5.1).
Отметим, что в любой точке потока вязкой жидкости касательные напряжения на взаимно перпендикулярных площадках, направленные по нормали к линии пересечения этих площадок, равны друг другу, т.е.

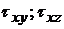
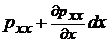

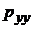

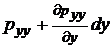
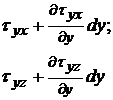


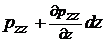

Таким образом, напряженное состояние вязкой движущейся жидкости характеризуется шестью независимыми компонентами напряжений рхх, руу, pzz, txy = tyx ; txz = tzx ; tyz = tzy.
Составим уравнения движения массы жидкости, заключенной в параллелепипеде (рис .5.1), рассмотрев сначала сумму проекций сил на направление оси ОХ. Эта сумма равна произведению массы параллелепипеда rdxdydz на проекцию ускорения движения его полюса (центра).
При составлении проекций принято считать направления нормальных напряжений совпадающими с направлениями внешних нормалей к граням параллелепипеда. В проекции на ось ОХ уравнение движения имеет вид
где Rxrdxdydz — проекция равнодействующей массовых сил на ось ОХ.
Произведя сокращения подобных членов, получим

Выполнив аналогичные действия для проекций сил на направления осей OY и OZ, получим систему дифференциальных уравнений движения вязкой жидкости в напряжениях:
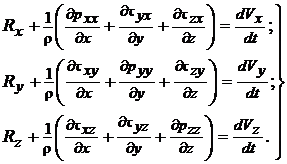
Если считать заданными проекции плотности распределения массовых сил, в уравнение (5.1) входят десять неизвестных функций: Vx, Vy, Vz, pхх, pyy, pzz, txy = tyx , txz = tzx, tyz = tzy .
Так как уравнений движения всего три, то система уравнений движения вязкой жидкости оказывается незамкнутой. Замыкание этой систеы уравнений может быть осуществлено с помощью уравнения неразрывности и других соотношений, устанавливающих связи между неизвестными. Обычно эти соотношения вводятся на основе гипотез и потому обязательно должны быть подтверждены экспериментально.
В основу получения соотношений между касательными напряжениями t и скоростями деформации жидких частиц в гидромеханике положен закон внутреннего трения Ньютона (1.18)
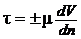
где µ — динамический коэффициент вязкости; 
Градиент скорости при слоистом движении жидкости выражает скорость угловой деформации частицы:


Распространяя закон вязкого трения на трехмерное (пространственное) движение, получим для касательных напряжений:
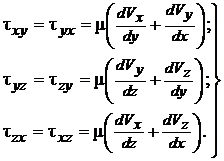
В каждой точке движущейся вязкой жидкости кроме касательных напряжений есть нормальные напряжения, значения которых зависят от направления действия. Последние являются следствием проявления вязкости и в гидромеханике описываются зависимостями
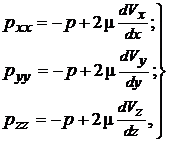
где р — давление, аналогичное давлению, действующему в невязкой жидкости, 
Добавочные напряжения не зависят от значения давления, но зависят от направления действия.

Перепишем уравнения (5.1), объединив в скобках все члены, зависящие от вязкости:
Подставив в эту систему уравнений значения напряжений из (5.2) и (5.3),а также выразив субстанциональное ускорение через локальное и конвективное ускорения (см. 3.4), получим систему уравнений движения вязкой несжимаемой жидкости ( = const) в виде:
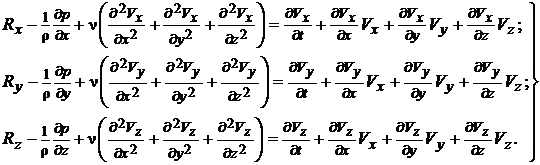
где ν — кинематический коэффициент вязкости.
Эти уравнения носят название уравнений Навъе-Стокса. Они записаны для неустановившегося движения несжимаемой вязкой жидкости.
Составляющие плотности распределения массовых сил Rx, Ry, Rz считаются заданными, а плотность r и кинематическая вязкость ν ( при соответствующем обосновании) — постоянными.
Тогда полученные уравнения совместно с уравнением неразрывности образуют замкнутую систему: при четырех уравнениях имеем четыре неизвестных функции p, Vx, Vy, Vz.
Общее решение нелинейных дифференциальных уравнений Навье-Стокса пока не найдено. Но в ряде случаев получены частные решения. Для этого должны быть заданы начальные и граничные условия.
Начальными условиями обычно задается распределение скоростей в области движения жидкости в некоторый момент времени. Это обычно удается практически осуществить только на основе экспериментальных данных.
Граничные условия задаются значениями скорости и давления на границах потока. На твердой границе используется условие прилипания частиц жидкости к твердому телу, т.е. например, на неподвижной твердой границе скорость потока будет равна нулю.
Границей потока может служить и свободная поверхность. В этом случае граничным условием является: давление во всех точках свободной поверхности одинаково и равно давлению во внешней среде.
Источник
Касательное напряжение возникающее в жидкости
Вопросы к зачету по группам МТ:
2.1. Основные свойства капельных жидкостей
2.2. Основные свойства газов
2.1. Основные свойства капельных жидкостей
1. Плотностью называют массу единицы объема жидкости. Для однородной жидкости плотность равняется величине массы М жидкости , поделенной на величину объема V , который она занимает
Плотность измеряется в системе СИ в кг/м 3 .
В системе СИ плотность воды при 4ºС составляет ρв = 1000 кг/м 3 , плотность рабочей жидкости МГ-30 при 20 ºС ρрж = 880 кГ/м 3 .
2. Удельным весом называют вес единицы объема жидкости. Для однородной жидкости удельный вес равняется величине веса G жидкости , поделенной на величину объема V , который она занимает
Удельный вес измеряется в системе СИ в Н/м 3 .
удельный вес воды при 4ºС составляет
удельный вес рабочей жидкости МГ-30 при 20 ºС составляет
γ = ρрж* g = = 880*9,81 = 8,64*10 3 Н/м 3 .
Связь между удельным весом γ и плотностью ρ известна
G = М g , γ V = ρ Vg , откуда γ = ρ g (2.3)
Отметим, что удельный вес воды в системе МКГСС равен γв = 1000 кГс/м 3 , а рабочей жидкости γрж = 880 кГс/м 3 .
Если жидкость неоднородна, то формулы (2.1) и (2.2) определяют средние значения удельного веса или плотности.
3. Вязкостью жидкости называется способность сопротивляться сдвигу ее слоев. При сдвиге слоев жидкости возникают касательные напряжения. Вязкость есть свойство противоположное текучести: более вязкие жидкости, сравниваемые с водой, такие как глицерин, смазочные масла являются менее текучими и наоборот.
При течении вязкой жидкости из-за тормозящего влияния неподвижного дна слои жидкости будут двигаться с разными скоростями, значения которых возрастает по мере удаления от твердого дна (рис. 2.1). Скорость V тем меньше, чем ближе слой жидкости к неподвижной стенке, при у = 0 , V = 0.
Рассмотрим два слоя жидкости, двигающиеся на расстоянии Δу. Слой А движется со скоростью V , слой В со скоростью V + Δ V . Из-за разности скоростей слой В сдвигается относительно слоя А на величину Δ V (за единицу времени). Величина Δ V является абсолютным сдвигом слоя А, а отношение Δ υ/Δ y – относительный сдвиг или градиент скорости. При сдвиге появляются касательные напряжения, которые обозначим через τ . Тогда аналогично явлению сдвига в твердых телах получим зависимость между напряжением и деформацией
Или, если слои будут расположены бесконечно близко друг к другу, переходим к дифференциалам, и получаем закон трения в жидкости Ньютона
Коэффициент пропорциональности μ в формуле для определения касательного напряжения в жидкости называется динамической вязкостью и характеризует сопротивляемость жидкости сдвигу.
Гипотеза о возникновении касательных напряжений между слоями жидкости была высказана Ньютоном, поэтому называется законом трения Ньютона. Экспериментально эта гипотеза была доказана профессором Н.П. Петровым в 1883 г .
Из закона трения выражаемого уравнением (2.1), следует, что напряжения трения возможно только в движущейся жидкости, вязкость проявляется при течении жидкости, в покоящейся жидкости касательные напряжения будем считать равными нулю.
Сила сопротивления сдвигу Т называется силой внутреннего трения, при постоянстве касательного напряжения по поверхности S выражается формулой Ньютона
Т = τ S = ± μ ( d υ/ dy ) S , (2.2)
где μ — тот же коэффициент пропорциональности, что и в формуле для касательного напряжения в жидкости. Знак перед значением силы выбирается в зависимости от знака градиента так, чтобы сила имела положительное значение.
Размерность динамической вязкости можем получить из формулы для касательного напряжения
В системе СИ единица динамической вязкости называется «Паскаль- секунда».
В системе СГС единица динамической вязкости называется «Пуаз» в честь французского врача Пуазейля, исследовавшего законы движения крови в сосудах.
Единица динамической вязкости
(сантиметр, грамм массы, секунда)
Наряду с понятием динамической вязкости в гидравлике используют понятие кинематической вязкости. Кинематическая вязкостью называется отношение динамической вязкости к плотности
В размерности кинематической вязкости отсутствуют единицы силы, ее легко измерить с помощью приборов носящих название вязкозиметров.
Единицей измерения кинематической вязкости с системе СИ является м 2 /с. В системе СГС единица измерения кинематической вязкости называется Стокс(Ст) в честь английского ученого Стокса, сотая доля стокса называется сантистоксом (сСт).
Единица кинематической вязкости
(сантиметр, грамм массы, секунда)
1 Ст = 10 -4 м 2 /с 1 сСт = 10 -6 м 2 /с
Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 2.2). Вязкость газов наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления.
Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает. В газах же вязкость обусловлена, главным образом, беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышением температуры. Поэтому вязкость газов с увеличением температуры возрастает.
Рис.2.2 Зависимость кинематической вязкости от температуры.
Обычно влияние температуры на вязкость оценивается с помощью таких экспериментальных графиков в справочной литературе. Однако, влияние температуры и давления на вязкость жидкостей можно оценить с помощью экспоненциальных зависимости, связывающей вязкость и температуру, а также давление и температуру.
Зависимость вязкости от давления проявляется лишь при относительно больших давлениях в несколько десятков МПа. С увеличением давления вязкость большинства жидкостей возрастает.
Рис.2.3. Зависимость относительной вязкости μ/μ0 от давления.
Где μ и μ0 — вязкость при давлении Р и Р0 ; α — коэффициент, значение которого для минеральных масел изменяется в пределах 0,02—0,03 (нижний предел соответствует высоким температурам, а верхний- низким). Например, известна вязкость воды при давлении 1 атм и 20 ºС, она равна 10 6 м 2 /с, определить вязкость воды при той же температуре и давлении 100 МПа, согласно графику она вырастет в 4 раза.
Наиболее распространенным является вискозиметр Энглера, который представляет собой цилиндрический сосуд, окруженный водяной ванной определенной температуры с насадком, встроенным в дно. Градус Энглера, назван по по имени немецкого химика Энглера, у нас он называется градус ВУ, внесистемная единица условной вязкости (ВУ) жидкостей, применяемая в технике. В России для измерения условий вязкости приняты условные градусы Энглера (°Е), которые представляют собой показания вискозиметра при 20, 50 и 100°С и обозначаются соответственно °E20;°E50 и °E100 .
Значение вязкости в градусах Энглера, например, °E20 есть отношение времени истечения t ж через отверстие вязкозиметра 200 см3 испытуемой жидкости к времени истечения такого же количества дистиллированной воды tв при 20 °С.
1 °E20 = t / t вод, где t вод = 51,6 с.
Для пересчета градусов Энглера в стоксы в случае минеральных масел применяют формулу
3. Сжимаемость — свойство жидкости изменять объем под действием давления, характеризуется коэффициентом объемного сжатия, который представляет собой относительное изменение объема Δ V при изменении давления ΔР на единицу давления, V 1 – первоначальный объем.
βр = — 
Коэффициент объемного сжатия в системе СИ измеряется в м 2 /Н или Па -1 .
Знак минус в формуле связан с тем, что увеличению давления Р2 >Р1 соответствует уменьшение объема V 2 V 1 . Рассматривая конечные приращения ΔР = Р2 — Р1 и
или, учитывая равенство ρ = m / V (1.4), находим приближенную формулу для определения плотности при увеличении давления
ρ2 ≈ ρ1 /(1— βр * Δр) (2.6)
обратная коэффициенту βр, называется объемным модулем упругости (ОМУ). Размерность ОМУ – Н/м 2 такая же, как размерность давления . Используя объемный модуль упругости К и конечные разности формулу (2.4) можно переписать в виде зависимости



которую называют обобщенным законом Гука.
Объемный модуль упругости К уменьшается с увеличением температуры и возрастает с повышением давления.
Для воды он составляет при атмосферном давлении приблизительно Кв = 2000 МПа. Следовательно, при повышении давления на 0,1 МПа (1 ат) объем воды уменьшается всего лишь на 1/20 000(одна двадцатитысячная) часть.
Такого же порядка модуль упругости и для других капельных жидкостей, например, для минеральных масел он равен приблизительно Крж = 1200 МПа.
Различают адиабатный и изотермический модуль упругости. Первый больше второго приблизительно в 1,5 раза и проявляется при быстротекущих процессах сжатия жидкости без теплообмена. Приведенные выше значения ОМУ являются значениями изотермического модуля.
Используя эти значения ОМУ по формуле (2.7), можно определить: при повышении давления воды до 40 МПа ее плотность повышается лишь на 2 %, а минерального масла на 3 %. Поэтому в большинстве случаев капельные жидкости можно считать практически несжимаемыми, т. е. принимать их плотность не зависящей от давления, но при очень высоких давлениях и упругих колебаниях сжимаемость жидкостей следует учитывать.
4. Температурное расширение характеризуется коэффициентом объемного расширения, который представляет собой относительное изменение объема при изменении температуры Т па 1°С и постоянном давлении, т. е.
βт = 
Рассматривая конечные приращения Δ V = V 2 — V 1 и ΔТ= Т2 — Т1 и, принимая βт постоянным, получаем объем жидкости при изменении температуры
учитывая равенство ρ = М/ V , находим приближенную формулу для определения плотности жидкости при изменении температуры
Для воды коэффициент βт возрастает с увеличением давления и температуры, при при 100°С и 10 МПа, βт = 700*10 -6 . Для минеральных масел в диапазоне давлений от 0 до 15 МПа βт можно принимать равным 800*10 -6 .
5. Сопротивление растяжению внутри капельных жидкостей по молекулярной теории может быть весьма значительно. При опытах с тщательно очищенной и дегазированной водой в ней были получены кратковременные напряжения растяжения до 23—28 МПа. Однако технически чистые жидкости, содержащие взвешенные твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначительных напряжений растяжения. Поэтому считают, что напряжения растяжения в капельных жидкостях невозможны.
5. Силы поверхностного натяжения. Свободная поверхность жидкости горизонтальна по всей поверхности раздела между жидкой и газообразной средой, кроме точек вблизи твердой стенки сосуда, где проявляются молекулярные силы взаимодействия твердого тела с жидкостью рис.2.4а. На поверхности раздела жидкости и воздуха действуют силы поверхностного натяжения, стремящиеся придать объему жидкости сферическую форму. Это явление проявляется также при выливании капли жидкости на твердую поверхность, рис.2.4б.
Поверхность у стенок сосуда искривлена (рис.2.4), и искривление сопровождается появлением дополнительного давления. В зависимости от того смачивается твердая поверхность жидкостью (рис.2г) или не смачивается (рис.2д) у твердой стенки жидкость может иметь разный краевой угол θ, соответствующий смачиванию или его отсутствию.
Трубка небольшого диаметра, в которой отсутствует горизонтальный участок поверхности раздела, называется капилляром. В этой трубке дополнительное давление может поднимать уровень жидкости (при смачивании) или опускать его.
Дополнительное давление, возникающее в капилляре определяется формулой
где σ — коэффициент поверхностного натяжения жидкости; r — радиус сферы, которая формируется в соответствие со свойствами жидкости и воздействием внешней среды.
Коэффициент σ, размерность которого Н/м, имеет следующие значения для разных жидкостей, граничащих с воздухом при температуре 20°С: для воды 73*10 -4 , для спирта
22*10 -4 , для керосина 27*10 -4 , для ртути 460*10 -4 . С ростом температуры поверхностное натяжение уменьшается.
Высоту подъема смачивающей жидкости или опускание несмачивающей жидкости в стеклянной трубке диаметром d определяют по формуле для полусферического мениска
где k (мм 2 ) имеет следующие значения: для воды 30, для ртути 10,1, для спирта +11,5.
С явлением капиллярности приходится сталкиваться при использовании стеклянных трубок в приборах для измерения давления, а также в некоторых случаях истечения жидкости. Большое значение приобретают силы поверхностного натяжения в жидкости, находящейся в условиях невесомости.
7. Испарение – процесс перехода жидкости в газообразное состояние. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова и зависит от условий, в которых они находятся.
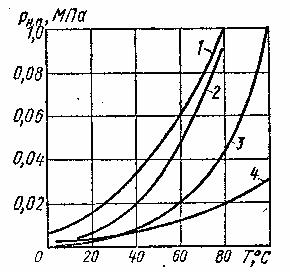
Рис.2.6 Зависимость давления насыщенных паров от температуры. 1 – бензин, 2 – спирт, 3- вода, 4 – керосин.
Если объем пространства над жидкостью достаточно велик испарение продолжается до исчезновения жидкости (выкипание чайника). Если объем недостаточно велик, часть молекул жидкости конденсируется и возвращается в жидкое состояние и испарение продолжается до наступления динамического равновесия, когда число испаряющихся и конденсирующихся молекул выравниваются. В окружающем жидкость пространстве устанавливается давление, называемое давлением насыщенных паров Рн.п. Одним из показателей характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении; чем выше температура кипения, тем меньше испаряемость жидкости.
Более полной характеристикой испаряемости является давление (упругость) насыщенных паров Рн.п. , выраженное в функции температуры. Чем больше давление насыщенных паров при данной температуре, тем больше испаряемость жидкости. С увеличением температуры давление Рн.п. увеличивается, однако у разных жидкостей в разной степени (рис. 2.6).
Для сложных жидкостей, представляющих собой многокомпонентные смеси, например, бензина или рабочая жидкость, содержащие растворенный воздух, давление Рн.п. зависит не только от физико-химических свойств и температуры но и от соотношения объемов жидкой и паровой фаз. Давление насыщенных паров возрастает с увеличением части объема занятого жидкой фазой. Обычно значения упругости паров сложных жидкостей даются для отношения паровой и жидкой фаз, равного 4: 1.
Максимально возможный в рабочей жидкости вакуум ограничен при данной температуре давлением насыщенных паров
8. Растворимость газов в жидкостях характеризуется количеством растворенного газа в единице объема жидкости, различна для разных жидкостей и изменяется с увеличением давления.
Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, т. е.
где V г — объем растворенного газа, приведенный к нормальным условиям, (Р0, Т0); V ж — объем жидкости; k — коэффициент растворимости; Р —давление жидкости.
Коэффициент k имеет следующие значения при 20 °С: для воды 0,016, керосина 0,13 минеральных масел 0,08, жидкости АМГ-10 — 0,1.
При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворятся в ней. Это явление может отрицательно сказываться на работе гидросистем.
9. Смазывающая способность – свойство жидкости обеспечивать наименьшее трение и износ металлических поверхностей деталей под нагрузкой. При пуске механизмов или при разрыве несущего слоя масляной пленки, неровности соприкасающихся деталей контактируют друг с другом, возникают значительные силы трения, если смазывающая способность не будет обеспечена. Оценка смазывающей способности затруднительна, но принимается во внимание при конструировании изделий гидравлики.
2.3. Основные свойства газов
Газы отличаются от жидкостей тем, что при большом давлении они могут быть сжаты до очень малого объема. Если предоставить любому газу большее пространство, чем он занимает, происходит расширение газа, а его давление уменьшается.
Закон, связывающий между собой давление и объем газа, впервые был открыт в начале 17-го века году Р.Бойлем, а позже Мариоттом.
Согласно этому закону давления одного и того же количества газа при постоянной температуре обратно пропорциональны объемам, занимаемым этим количеством газа.
Кривая зависимости Р от V называется изотермой.
Давление газа зависит также и от температуры. Гей-Люсак в 1816 году нашел, что эта связь выражается формулой при Р – const , закон Гей –Люсака(изобарный)
где V 0 – объем газа при 0°С, t – температура в градусах Цельсия, α =1/273 – термический коэффициент расширения. В это уравнение давление не входит, так как оно при сравниваемых состояниях газа одинаково.
Клайперон, связав законы Бойля-Мариотта и Гей-Люсака, получил уравнение состояния идеальных газов
где ( PV ) /Т = В – удельная газовая постоянная, различная для различных газов.
Реальные газы также соответствуют этому закону при обычных плотностях и при небольшом сжатии газа. При очень быстром сжатии (нагревание) или расширении (охлаждение) — (адиабатические процессы) Бойля-Мариота выражается степенной зависимостью 
где η = C р/ Cv — теплоемкости при постоянном давлении и при постоянном объеме.
Показатель степени равен η =1,4 для воздуха, для других газов он близок к этому значению.
Источник