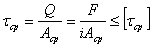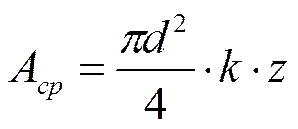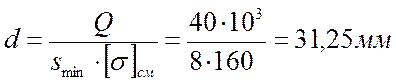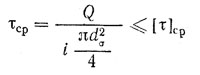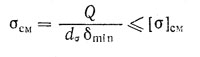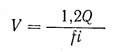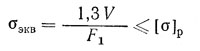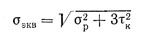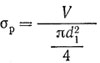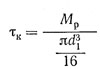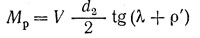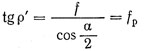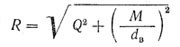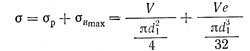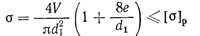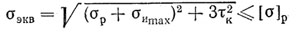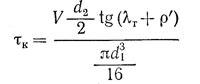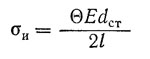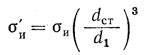Касательные напряжения среза болта

Rimoyt.com

Темы: машиностроение, САПР, 3d моделирование, техническое образование, промышленные предприятия, технические вузы

Истина подобна небу, а мнения — облакам.

Срез — разрушение соединительных деталей под действием поперечных нагрузок (т.е. перпендикулярных осям этих деталей).

Например, разрушение штифта может произойти при штифтовом соединении двух деталей, которые нагружены двумя противоположно направленными силами. Вместо штифта может быть шпонка, болт, шпилька, заклепка.

Допущения при расчете на срез:
— в поперечном сечении детали, где может быть срез, возникает только поперечная сила Q
— касательные напряжения распределены по поперечному сечению равномерно
— при соединении несколькими одинаковыми деталями – все они нагружены одинаково

Условие прочности при расчете на срез:

— расчетное напряжение среза
Q = F/i – поперечная сила в сечении
i – число соединительных деталей (например, число заклепок)
Aср – площадь поперечного сечения срезаемой детали (заклепки)
— допускаемое напряжение

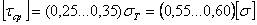
Три вида расчетов на срез:
— проверочный
— проектировочный – определение числа соединительных деталей или размеров деталей
— определение допускаемой нагрузки

Смятие – разрушение от давления между поверхностями соединительной детали и отверстия (при штифтовом, шпоночном соединениях и т.д.). При изменении формы отверстия от давления соединение разрушается.

Допущения при расчете на срез:
— силы давления распределены по поверхности смятия равномерно
— силы давления перпендикулярны поверхности смятия

Условие прочности при расчете на смятие: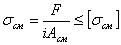

F/i – нагрузка на один соединительный элемент
i – число соединительных элементов
Aсм – площадь смятия

— допускаемое напряжение

Источник

Расчет болтовых соединений на срез и смятие.

СРЕЗ, СМЯТИЕ.

Болтовые соединения используются в фермах, металлических балочных конструкциях, колоннах и других конструкцияхдля крепления двух или трех отдельных элементов между собой.

При соединении элементов на каждый болт передаются две равные и противоположно направленные силы от первого и второго элементов (рис.а). Болт перерезается в плоскости соединения двух элементов, силы от которых образуют пару, уравновешиваемую другой парой сил – реакцией со стороны головки и гайки болта. Однако эти реакции не опасны, ибо для изготовления болтов используются высококачественная сталь.

Два элемента могут также соединяться с использованием одной или двухнакладок. Схема распределения усилий при наличии двух накладок указана на рис. б. В этом случае болт перерезается в двух плоскостях.

Прирешении задачи на срез и смятие необходимо :

1. Определить диаметр соединительного элемента (болта, заклепки, штифта и т.п.) используя условие прочности на срез:

где τ_ср – расчетное напряжение среза в плоскости рассчитываемого сечения;

[ τ ]_ср – допускаемое напряжение при срезе (сдвиге);

A_ср – площадь среза соединительного элемента:

k – число плоскостей среза в одном соединительном элементе (болте, заклепки, штифте и т.п.)

z – число соединительных элементов (болтов, заклепок, штифтов и т.п.);

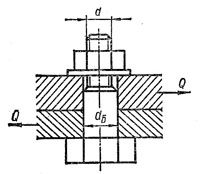
Рис. 1 — Зоны возникновения напряжений среза и смятия

2. Определить диаметр соединительного элемента (болта, заклепки, штифта и т.п.) используя условие прочности на смятие:

где σ_см– расчетное напряжение смятия;

[ σ ]_см – допускаемое напряжение смятия;

Q – поперечная сила (при передаче силы F при нескольких соединительных элементах Q = F / z);

z – число соединительных элементов (болтов, заклепок, штифтов и т.п.);

Из допущения о характере распределения сил взаимодействия по поверхности контакта следует, что если контакт осуществляется по поверхности полуцилиндра, то расчетная площадь А_см равна площади проекции поверхности контакта на диаметральную плоскость, т.е. равна диаметру цилиндрической поверхности d на ее минимальную высоту s:

3. Принять наибольшее значение диаметра соединительного элемента (болта, заклепки, штифта и т.п.)

Пример 1.Определить, исходя из условий прочности на срез и смятие, необходимый диаметр болта в соединении , показанном на рисунке 2. К листам приложена растягивающая сила F = 40 кН. Толщина одного листа 8 мм, второго листа — 10 мм. Материал болта — Ст3. Допускаемое напряжение на срез [t]_ср = 80 МПа. Допускаемое напряжение на смятие [σ]_см = 160 МПа. Болт без зазора входит в отверстие.

1. Определяем диаметр болта используя условие прочности на срез:

d=√4F/ πkz[t]ср

2. Определяем диаметр болта используя условие прочности на смятие:

Из двух значений диаметра, найденных по условиям прочности на срез и смятие, следует принять большее, т.е. d ³ 31,25 мм.

Согласно ГОСТ 24705-2004 Резьба метрическая надо взять болт с номинальным диаметром 32 мм.

Задача С-6. Стальные листы соединены между собой при помощи болтов, плотно вставленных в отверстия. К листам приложены растягивающие силы F. Материал болтов — Ст3. Допускаемое напряжение на срез [t]_ср = 80 МПа. Допускаемое напряжение на смятие [σ]_см = 160 МПа. (рисунок 4). Определить диаметр болтов. Данные своего варианта взять из таблицы 1

Источник

Техническая механика

Сопротивление материалов

Сдвиг (срез)

Напряжения при сдвиге

Сдвигом называют такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила.
Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков, при пробивании отверстия в заготовках на штампе (рис. 1) .

Рассмотрим брус площадью поперечного сечения А , перпендикулярно оси которого приложены две равные и противоположно направленные силы F ; линии действия этих сил параллельны и находятся на относительно небольшом расстоянии друг от друга.
Для определения поперечной силы Q применим метод сечений (рис. 2) .
Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:

откуда поперечная сила Q может быть определена, как:

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении бруса при сдвиге.
Очевидно, что при сдвиге в поперечном сечении возникают только касательные напряжения τ .

Предполагаем, что эти касательные напряжения равномерно распределены по сечению, и, следовательно, могут быть вычислены по формуле:

На основании полученной формулы можно сделать вывод, что форма сечения на величину напряжения при деформации сдвига не влияет.

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое.
Расчетная формула при сдвиге:

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое . (при обозначении предельно допустимых напряжений применяют квадратные скобки: [τ] или [σ] )
По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам).
Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести.
В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают [τ_ср] = (0,25….0,35) σ_т, где σ_т – предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

Деформация Гука при сдвиге

Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abcd , на грани которого действуют только касательные напряжения τ , а противоположную грань параллелепипеда представим жестко защемленной (рис. 3) .

Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bc по отношению к сечению, принятому за неподвижное.
Деформация сдвига характеризуется углом γ (гамма) и называется углом сдвига , или относительным сдвигом . Величина bb₁ , на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом .
Относительный сдвиг γ выражается в радианах.

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется закон Гука при сдвиге.
Закон Гука при сдвиге справедлив лишь в определенных пределах нагрузок и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу .

Математически закон Гука для деформации сдвига можно записать в виде равенства:

Коэффициент пропорциональности G характеризует жесткость материала, т. е. способность сопротивляться упругим деформациям при сдвиге, и называется модулем сдвига или модулем упругости второго рода .

Модуль упругости выражается в паскалях; для различных материалов его величина определена экспериментально и ее можно найти в специальных справочниках.
При проведении ответственных расчетов на срез величина модуля упругости для каждого соединения определяется опытным путем, непосредственно перед расчетом, либо берется из справочника с применением увеличенного запаса прочности.

Следует отметить, что между тремя упругими постоянными (модулями упругости) E , G и ν существует следующая зависимость:

Принимая для сталей ν ≈ 0,25, получаем: G_ст ≈ 0,4 Е_ст .

Материалы раздела «Сопротивление материалов»:

Источник

Расчет резьбовых крепежных изделий при постоянных напряжениях

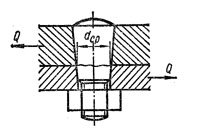
Болт поставлен без зазора в отверстие из-под развертки

Силы, перпендикулярные к оси болта, вызывают срез. Условие прочности болта

где τ_ср — расчетное напряжение на срез, Н/мм 2 ;
τ_ср — (0,2 — 0,3)σ_t —допускаемое напряжение на срез;
σ_t — предел текучести материала болта, Н/мм 2
Q — сила, действующая на соединение, Н;
i — число плоскостей среза (на рисунке i = 1);
d _б — диаметр ненарезанной части болта, мм.
Поверхности контакта соединяемых деталей и ненарезанной части болта проверяют на смятие:

σ_см — расчетное напряжение смятия, Н/мм 2 ;
δ _min — наименьшая толщина соединяемых деталей, находящихся в контакте с болтом мм;
[σ] _см — допускаемое напряжение смятия, Н/мм 2 :
для стали углеродистой [σ] _см — (0,8 — 1,0)σ _т ;
для стали легированной [σ] _см — (0,6 — 0,8)σ _т
для чугуна [σ] _см — (0,6 — 0,8)σ _пчр

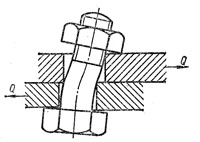
Расчет прецизионных (призонных) болтов, которые вставляют в конические отверстия

Болт, поставленный с зазором, воспринимает нагрузку, перпендикулярную к оси

Силу, с которой нужно затянуть болт — ее называют силой затяжки и определяют из условия, — чтобы не было сдвига деталей, т. е. чтобы сила трения Т на стыках соединяемых деталей была не меньше сдвигающей силы, обычно принимают с учетом запаса против сдвига деталей T = 1,2Q.

Для болта в данном соединении требуемая сила затяжки

где Q — сдвигающая сила;
i — число стыков ( i = 1);
f — коэффициент трения для стыка.
Для сухих обработанных стыков стальных или чугунных деталей
f = 0,10…0,15; то же при наличии масляной пленки f = 0,06.
В стыках стальных конструкций:
при пескоструйной обработке стыка f = 0,5;
при обработке пламенем газовой горелки f = 0,4;
при необработанных стыках (со следами окалины) f = 0,3;
при окраске алюминиевым порошком f = 015;
при окраске антикоррозионной краской f = 0,10;
при окраске свинцовым суриком f = 0,06

По найденной силе затяжки V рассчитывают болт на совместное действие растяжения и кручения. На практике влияние кручения для стандартных метрических резьб учитывают приближенно, вводя коэффициент 1,3. Тогда условие прочности

где F₁ = πd 2 ₁/4 — площадь поперечного сечения по внутреннему диаметру резьбы, мм 2 ;
[σ]_p = σ _т/ [n] — допускаемое напряжение, Н/мм 2
σ _т — предел текучести материала болта, Н/мм 2 ;
[n] — требуемый коэффициент запаса:
при контролируемой затяжке для болтов из углеродистой стали [n] = 1,6; для болтов из легированной стали [n] = 2
при неконтролируемой затяжке коэффициенты запаса [n] принимают в зависимости от диаметра резьбы:

Значения [n] при номинальном диаметре резьбы d, мм

Материал болтов	Ø 6 — 16	Ø 16 — 30	Ø 30 — 60
Углеродистая сталь	5 — 4	4 — 2,5	2,5 — 1,7
Легированная сталь	6,5 — 5	5 — 3,3	3,3 — 3

На практике чаще приходится иметь дело с неконтролируемой затяжкой. Поэтому для затянутых болтов с резьбой от М6 до М48 при неконтролируемой затяжке подсчитаны допускаемые осевые нагрузки [Р], которые приведены в таблице

Допускаемые осевые нагрузки [P] в кН для затянутых болтов при неконтролируемой затяжке

Материал	Ст 3	Сталь 35	Сталь 45	12ХН2	40Х
σ т, Н/мм 2	210	320	360	600	800
М6	0,80	1,20	1,35	1,75	2,30
М8	1,45	2,20	2,50	3,20	4,20
М10	2,55	3,90	4,40	5,50	7,30
М12	3,70	5,70	6,40	8,00	10,50
(М14)	5,75	8,80	9,90	13,00	17,50
М16	7,90	12,00	13,50	18,00	24,00
(М18)	9,60	14,50	16,50	22,00	29,50
М20	14,00	21,50	24,00	31,00	41,00
(М22)	20,00	31,00	35,00	43,00	58,00
М24	23,50	36,00	40,00	50,00	67,00
(М27)	37,00	56,00	63,00	80,00	105,00
М30	45,00	69,00	77,00	98,00	130,00
М36	73,00	110,00	125,00	145,00	195,00
М42	100,00	150,00	170,00	200,00	270,00
М48	130,00	235,00	255,00	275,00	365,00

Примечание. Размеры болтов, заключенные а скобки, применять не рекомендуется

Уточненный расчет

При более точных расчетах определяют эквивалентное напряжение

где, напряжение растяжения в поперечном сечении нарезанной части болта

наибольшее напряжение кручения в поперечном сечении нарезанной части болта

d₂ — средний диаметр резьбы;
λ — угол подъема резьбы;
ρ ‘ — приведенный угол трения, определяемый из соотношения

условный коэффициент трения между витками резьбы с углом профиля а или иначе приведенный коэффициент трения.

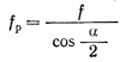
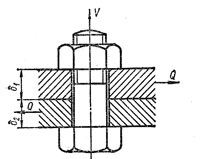
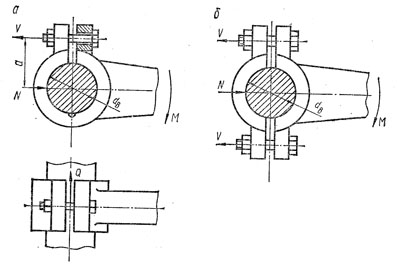
Болты клеммового (фрикционно — винтового) соединения

а — клемма с разрезной ступицей; б — клемма с разъемной ступицей

Эти болты также ставятся с зазором. Их затягивают так, чтобы момент трения М _тр на стыке вала и клеммы был не меньше вращающего момента М; обычно принимают с учетом запаса сцепления М _тр=1,2М

В общем случае клеммы могут быть нагружены одновременно осевой силой Q и вращающим моментом М. Клемма с разрезной ступицей менее удобна, чем клемма с разъемной ступицей. Последнюю можно устанавливать в любой части вала, не трогая насаженных на вал деталей.
Требуемая сила затяжки болтов клеммовых соединений зависит от принятого закона распределения давлений на поверхности контакта ступицы клеммы и вала. Наиболее неблагоприятной является посадка клеммы с большим зазором, когда контакт полуступиц с валом происходит по линиям; при затяжке болтов линейный контакт переходит в контакт по узкой площадке. При небольших зазорах, что соответствует в незатянутом состоянии посадкам h6 или g6, после затяжки закон распределения давлений оказывается близким к косинусоидальному. Наличие натяга в незатянутом соединении, что соответствует посадкам r6 или n6, обеспечивает после затяжки примерно равномерное распределение давлений

Рассматривается общий случай действия осевой силы Q и вращающего момента М. Расчет ведут либо по равнодействующей осевой и окружной сил, приведенной к поверхности контакта

либо отдельно по моменту М, стремящемуся повернуть клемму, и по силе Q, стремящейся сдвинуть клемму по валу.

Необходимая сила V затяжки болта

Клемма с разрезной ступицей и одним болтом (рис. а)	Клемма с разъемной ступицей и двумя болтами (рис. б)
Контакт по узкой площадке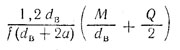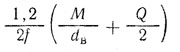
Посадка с малым зазором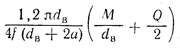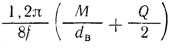
Посадка с натягом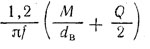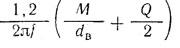

Винт нагружен осевой силой Q; возможно подтягивание под нагрузкой

Винты стяжных устройств работают на растяжение от внешних сил Q и на кручение от момента в резьбе М _р

Расчет на прочность проводят по формуле

с заменой V на Q.

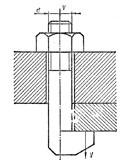
Болт с внецентренной растягивающей нагрузкой

При затяжке такой болт, имеющий эксцентричную или костыльную головку, испытывает растяжение, изгиб и кручение

Наибольшее суммарное нормальное напряжение

При значительных эксцентриситетах (е >0,1d) влияние кручения мало и его не учитывают. Тогда условие прочности

Изгиб болта (шпильки) может вызываться не только эксцентричностью нагружения, обусловленного формой головки болта, но и возникать из-за перекоса опорных поверхностей. Так, при перекосе торца гайки напряжения изгиба в поперечном сечении стержня шпильки

где Θ = Ml/EJ — угол перекоса в радианах;
Е — модуль продольной упругости материала шпильки;
d _ст — диаметр стержня шпильки;
l — длина шпильки
Напряжения изгиба в поперечном сечении нарезанной части шпильки

Из формулы следует, что для уменьшения напряжений σ _и‘ необходимо изготовлять шпильку с возможно меньшим диаметром стержня d _cт

Затянутый болт дополнительно нагружается осевой нагрузкой

Крепление крышек двигателей внутреннего сгорания, автоклавов и сосудов, находящихся под внутренним давлением.
Болты такого соединения должны быть при монтаже затянуты так сильно, чтобы гарантировать герметичность после приложения осевой нагрузки.

При соединении стальных или чугунных деталей ориентировочный расчет болта можно проводить на растяжение силой
Р = 1,3Q
где Р — осевая сила, действующая на болт, от предварительной затяжки;
Q — внешняя осевая сила

Источник