Коэффициент эквивалентности по контактным напряжениям

Определение допускаемых напряжений

Первоначально определение допускаемых контактных [ ]_Н и изгибных [ ]_F напряжений производим отдельно и для шестерни, и для колеса. Для этого находим:

1. Ресурс работы передачи в часах

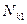
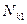
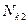
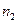
2. Ресурс работы передачи в числе циклов перемены напряжений на зубьях шестерни и колеса

=60 L_h; =60 L_h (21)

Марка стали	Термообработка	Твердость зубьев на поверхности	σТ, МПа
Нормализация	152-207НВ
167-217 НВ
50Г	190-229 НВ
30ХГС	215-229 НВ
40Х	200-230 НВ
Улучшение	207-250 НВ
50Г	241-285 НВ
30ХГС	235-280 НВ
40Х	257-285 НВ
40ХН	269-302 НВ
40Х	Улучшение + закалка ТВЧ	45-50HRC
40ХН,	48-53 HRC
35ХМ
40ХНМА	Азотирование	50-56 HRC
38Х2МЮА
20Х, 18ХГТ, 25ХГМ, 12ХН3А	Цементация и закалка	56-63 HRC

3. Коэффициенты эквивалентности по контактным μ_н и изгибным μ_F напряжениям для шестерни. Для типового режима нагружения (рис.2а) коэффициент эквивалентности принимают по таблице 2.2, для не типового, заданного циклограммой нагрузок (рис.2б), рассчитывают по формулам:

, (22)

где — вращающий момент, действующий в течение количества циклов ;

— кратковременный момент перегрузки с количеством циклов за срок службы менее 50*10 3 циклов

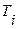
m—показательстепени кривой усталости (6 — для улучшенных и нормализованных сталей,9 — для других термообработок).

Рис.2. Циклограммы моментов (нагрузок)

4. Эквивалентные числа циклов нагружения зубьев шестерни и колеса за срок службы передачи соответственно по контактным и изгибным напряжениям.

, , (23)

, (24)

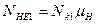
Таблица 2.2. Значения коэффициентов эквивалентности для типовых режимов нагружения

Режим нагружения	Коэффициент эквивалентности
μн	μF
m=6	m=9
постоянная нагрузка — 0
тяжелый — I	0,5	0,3	0,2
средний равновероятный — II	0,25	0,143	0,1
средний нормальный — III	0,18	0,065	0,036
легкий — IV	0,125	0,038	0,016
особо легкий — V	0,063	0,013	0,004

5. Коэффициенты долговечности по контактным напряжениям и по напряжениям изгиба

, (25)

где — базовое число циклов нагружения (для сталей с твердостью Н 7 , при твердости колес Н>350 HB (10НВ≈1 HRC)=30HB 2,4 ≤ 12*10 7 );

= 4_*10 6 – базовое число циклов по напряжениям изгиба;

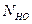
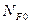
Область значений коэффициентов:

K_HL в диапазоне 1…2,6 для материалов с однородной структурой и 1…1,8 для поверхностно-упрочненных);

K_FL в диапазоне 1…4 для сталей с объемной термообработкой и 1…2,5 для сталей с поверхностной обработкой

6. По табл. 2.3 для шестерни и колеса находим пределы контактной σ_Hlim и изгибной выносливости σ_Flim

Таблица 2.3. Пределы контактной и изгибной выносливости

Термическая или химико- термическая обработка	Твердость поверхностей	Стали	σHlim , МПа	σFlim , МПа
Улучшение, нормализация	≤350НВ	Углеродистые и легированные стали	2НВ+70	1.75НВ
Объемная закалка	38-50HRC	17HRC+100	500-550
Поверхностная закалка	40-56HRC	17HRC+200	600-700
Цементация и закалка	56-63HRC	Легированные стали	23HRC	750-800
Азотирование	56-65HRC	Азотируемые стали	12HRC+290

7.Допускаемые контактные напряжения (МПа) вычисляют для шестерни 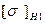и для колеса

= ,(26)

где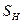— коэффициент безопасности (запаса прочности), принимаемый равным 1,1 при улучшении и нормализации и 1,2 при поверхностных упрочнениях;

Для зубчатых передач в качестве расчетных принимают меньшее из [σ]_H1 и [σ]_H2

8. Допускаемые напряжения изгиба σ_Flim (МПа) определяют по формулам

= ,(27)

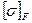
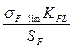
где S_F — коэффициент безопасности, выбираемый в зависимости от стабильности свойств материала, технологии изготовления и ответственности конструкции; для стальных зубчатых колес 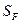= 1.4…2.2, в среднем 1.7;

9. Находим предельные допускаемые напряжения для проверки при перегрузке. Допускаемые напряжения [σ_Hmax] принимают при:

улучшении или сквозной закалке	[σHmax]=2,8 σт
цементации или контурной закалке ТВЧ	[σHmax]= 44НRСср
азотировании	[σHmax]=35НRСср≤2000МПа

Допускаемые напряжения [σ_Fmax] вычисляют также в зависимости от вида термообработки и возможной частоты приложения перегрузки:

где σ_Flim – предел выносливости при изгибе; Y_Nmax — максимально возможное значение коэффициента долговечности (4 для сталей с объемной термообработкой; 2,5 для сталей с поверхностной обработкой); k_st – коэффициент влияния частоты приложения перегрузки (1,2..1,3 перегрузки единичные, 1 при многократном (10 3 ) действии перегрузок.

Источник

Детали машин

Основы расчета на прочность зубчатых колес

Условия работоспособности зубчатых передач

Передача нагрузки в зубчатой передаче происходит в результате соприкосновения боковых профилей сопряженных зубьев. Под действием сил давления зубья находятся в сложнонапряженном состоянии. При этом нагружается и поверхность зубьев (линейный контакт), и весь объем зуба. Поэтому работоспособность передачи оценивается контактной прочностью боковой поверхности зубьев и объемной прочностью зуба при сложном нагружении. Оценка прочности зубьев усложняется действием переменной нагрузки на зуб, изменяющейся по прерывистому пульсирующему циклу.

При недостаточной контактной прочности поверхности зубьев происходит усталостное выкрашивание рабочих поверхностей.
Поломки зубьев в основном тоже носят усталостный характер и происходят либо при перегрузках передачи, либо при недостаточной их объемной прочности. При объемном нагружении зубьев главным видом деформации является изгиб. Поэтому оценку объемной прочности зубьев обычно проводят по деформации изгиба. Таким образом, в зубчатых передачах при оценке работоспособности используют два условия:

а) условие контактной прочности поверхности :

б) условие объемной прочности при деформации изгиба :

Таким образом, стандартный расчет зубчатых передач на прочность сводится к определению действующих в материалах колес напряжений (контактных и деформации изгиба) и сравнения полученных значений с допускаемыми напряжениями для этих материалов.

Сложность расчетов зубчатых колес на прочность обусловлена характером нагрузки, действующей в зоне контакта колес. Определение величины этой нагрузки, называемой расчетной нагрузкой – наиболее сложная задача, выполняемая при расчетах зубчатых передач. Ответственным этапом при расчетах вызывает правильная оценка допускаемых напряжений в зоне контакта зубьев.

Оптимизация параметров передачи

Стандартная зубчатая передача с эвольвентным зацеплением обеспечивает неразрывность контакта сопряженных зубьев в процессе работы и постоянное передаточное отношение в пределах допустимой погрешности. Для такой передачи основной критерий работоспособности – обеспечение контактной и изгибной прочности зубьев.
Кроме того, в условия работоспособности необходимо внести ряд существенных дополнений, учитывающих специфику нагружения, особенности конструкции и условий эксплуатации, позволяющих оптимизировать параметры проектируемой передачи – ее габариты, вес, стоимость изготовления.
Наиболее часто при проектировании передачи учитываются следующие условия оптимизации параметров:

• минимальное число зубьев;
• минимальное отклонение передаточного отношения;
• обеспечение стандартных значений модуля и межосевого расстояния;
• снижение до минимума неравномерности распределения нагрузки по длине зуба за счет минимизации ширины венца;
• минимальный угол наклона зубьев из условия торцевого перекрытия;
• минимальная масса и момент инерции колес;
• оптимальные коэффициенты смещения инструмента из условия наибольшей прочности зуба;
• оптимальные твердость и марка материала из условий эксплуатации.

Режимы нагружения

При работе зубчатой передачи зубья, входя поочередно в зацепление, подвергаются нагружению по прерывистому отнулевому циклу. Если параметры цикла неизменны во времени, то режим нагружения называют постоянным.

Большинство зубчатых передач работает при переменных режимах нагружения, которые задают циклограммой , т. е. графиком изменения вращающего момента Т (нагрузки) во времени (рис. 1).

Исследованиями и практическими испытаниями установлено, что при всем многообразии циклограмм моментов их можно приближенно свести к шести стандартным типовым режимам нагружения для большинства машин.

При вычерчивании графиков типовых режимов нагружения фактическую циклограмму (рис. 1, а) заменяют упорядоченной циклограммой (рис. 1, б), на которой вращающие моменты Т_i , действующие в течение требуемого ресурса N_K , располагают последовательно в порядке убывания их значений.

Затем строят эту циклограмму (рис. 2) в относительных координатах Т_i/Т_max , Σ N_i/N_K и полученную ступенчатую циклограмму заменяют плавной огибающей кривой. Так получают графическое изображение шести типовых режимов нагружения, которые на рис. 2 обозначены:

0 – постоянный режим нагружения – является наиболее тяжелым. его принимают за расчетный для неопределенных режимов нагружения (например, редуктор общего назначения может быть использован в различных нестандартных условиях). К режимам постоянного нагружения относят режимы с отклонениями до 15%. При этом за расчетную принимают нагрузку, соответствующую номинальной мощности двигателя.

I – тяжелый режим нагружения – характерен для машин, которые работают бόльшую часть времени с нагрузками, близкими к номинальным, например, для горных машин.

II – средний равновероятный режим нагружения – характерен для машин, которые работают одинаковое время при всех значениях нагрузок, например, для транспортных машин.

III – средний нормальный режим нагружения – характерен для машин, которые работают бόльшую часть времени при средних нагрузках, например для достаточно интенсивно эксплуатируемых машин.

IV – легкий режим нагружения – характерен для машин, которые работают бόльшую часть времени с нагрузками ниже средних, например для широко универсальных металлорежущих станков.

V – особо легкий режим нагружения – характерен для машин, которые работают бόльшую часть времени с малыми нагрузками, например, для металлорежущих станков.

Использование перечисленных выше типовых режимов нагружения позволяет упростить прочностные расчеты передач, в т. ч. – зубчатых.

В расчетах зубчатых передач на выносливость фактический переменный режим нагружения заменяют эквивалентным (по усталостному воздействию) постоянным режимом.

Чтобы понять значение эквивалентного режима работы предположим, что зубья колеса работают в переменном режиме, имеющем несколько ступеней, и на каждой i -й ступени испытывают N_i циклов нагружения. Опытным путем установлено, что разрушение зубьев при действии циклических напряжений происходит после суммы Σ N_i циклов нагружений в результате постепенного накопления в материале микроскопических дефектов и повреждений (микротрещин, раковин и т. п.).

При работе на нескольких ступенях нагружения повреждения продолжают независимо нарастать по линейному закону, поэтому их можно линейно суммировать.

Следовательно, фактический переменный режим нагружения можно заменить эквивалентным постоянным режимом, при котором зубья колеса приобретают равноценную степень усталостного повреждения.

В качестве эквивалентного принимают постоянный режим с номинальным моментом Т , равным наибольшему из длительно действующих моментов (на рис. 1 Т = Т_max = Т_З ) и эквивалентным числом циклов нагружения N_E .

Эквивалентные числа циклов нагружения N_НЕ и N_FE при расчете на контактную и изгибную прочность определяют соответственно по формулам:

где μ_Н и μ_F – коэффициенты эквивалентности для типовых режимов нагружений (табл. 1).

Таблица 1. Значение коэффициентов эквивалентности μ_Н и μ_F

В таблице 1 q_F — показатель степени уравнения кривой усталости при изгибе: для нормализованных и улучшенных колес q_F = 6, для закаленных и поверхностно упрочненных зубьев q_F = 9.

Требуемый ресурс N_K рассчитываемого зубчатого колеса в циклах при частоте вращения n , об/мин, и времени работы L_h , ч:

где n_З – число зацеплений зуба рассчитываемого колеса за один его оборот (численно равно числу колес, находящихся в зацеплении с рассчитываемым колесом).

Методика расчета зубчатых колес на прочность

Определение действительных контактных напряжений

При оценке работоспособности по условию контактной выносливости (1) необходимо вычислить фактические контактные напряжения, возникающие на боковых поверхностях зубьев. Экспериментальные исследования показывают, что разрушение профилей зубьев начинается в местах, расположенных в зоне начальных окружностей.
Для определения контактных напряжений можно воспользоваться формулой Герца для вычисления максимального нормального напряжения в зоне соприкосновения двух цилиндров по линейному контакту:

где q – нагрузка на единицу длины линии контакта (удельная нагрузка); q = F_tK_Н/b_w ,
здесь K_Н – коэффициент нагрузки; b_w – рабочая ширина зубчатого колеса;
Е_пр – приведенный модуль упругости, получаемый из соотношения 2 /Е_пр = 1 /Е₁ + 1 /Е₂ ; (здесь 1 /Е — некоторая характеристика податливости материала), откуда: Е_пр = 2 Е₁Е₂/(Е₁ + Е₂) ; для колес, изготовленных из одного материала, Е_пр = Е ;
ν — коэффициент Пуассона;
ρ_пр – приведенный радиус кривизны цилиндров, определяемый из соотношения 1 /ρ_пр = 1 /R₁ + 1 /R₂ , (здесь 1 /ρ_пр — кривизна поверхности), откуда: ρ_пр = R₁R₂ / (R₁ + R₂) .

Выразив величину напряжений через нагрузку и характеристики сопрягаемых поверхностей зубьев в зоне контакта, и введя коэффициент нагрузки K_Н для компенсации неучтенных других видов напряжений, получим формулу для определения действительных контактных напряжений работе зубчатой передачи.

Определение действительных напряжений при изгибе зубьев

При оценке напряжений изгиба принимают, что зуб ведомого колеса испытывает наибольшие напряжения в начале зацепления, а вся нагрузка передается одной парой зубьев в течение всего периода зацепления. Экспериментальные исследования показывают, что ошибки изготовления, приводящие к расхождению окружных шагов, не компенсируются полностью деформациями зубьев. В результате наиболее нагруженными зубья будут в начале и в конце зацепления.

Расчетную схему зуба можно представить в виде жестко защемленной балки, нагруженной нормальной силой F , приложенной к вершине зуба. Возникающая сила трения F_тр между зубьями приводит к отклонению силы нормального давления на угол трения α .
Величину силы F’ находят по формуле F’ =F/cos α .
Полученную силу F’ раскладывают на продольную и поперечную составляющие. Продольная составляющая N вызывает в зубе деформацию сжатия, а поперечная Q – деформации сдвига и изгиба.

Таким образом, зуб испытывает сложную деформацию. Однако напряжения сжатия малы по сравнению с напряжениями изгиба. Поэтому суммарные нормальные напряжения в опасном сечении зависят в основном от напряжений изгиба, уменьшенных на величину напряжения сжатия. Обычно расчет зуба ведут по той стороне зуба, на которой находят растянутые волокна, так как там быстрее появляются усталостные трещины.
Выразив величину напряжений через нагрузку и характеристики сечения и введя коэффициент нагрузки K_F для компенсации неучтенных других видов напряжений, определяют действительные напряжения при изгибе зубьев:

где l – плечо изгиба (расстояние от ножки зуба до опасного сечения;
W_З –момент сопротивления изгибу опасного сечения ножки зуба.

Расчетная нагрузка

Каждый зуб колеса можно условно представить в виде балки, подверженной во время работы динамическим нагрузкам отнулевого цикла. Эти нагрузки вызывают контактные напряжения в материале зуба, обусловленные криволинейностью рабочей поверхности зубьев, и изгибающие напряжения из-за пульсирующих поперечных нагрузок.
Длительное воздействие пульсирующих контактных напряжений и напряжений, обусловленных изгибом, вызывает усталость материала колеса, что приводит к различным повреждениям – разрушению рабочей поверхности зуба или даже его поломке.

Следует учитывать, что зубья колес, в отличие от принимаемых при расчетах в сопромате элементарных балок, подвержены сложным нагружениям, поэтому их прочностной расчет сопровождается учетом многочисленных факторов, влияющих на величину нагрузки на зубья во время работы передачи. При работе зубчатых колес в их зацеплении возникают дополнительные нагрузки, связанные с условиями эксплуатации, погрешностями в изготовлении и монтаже, деформациями валов и опор и др. Влияние этих факторов на прочностные свойства зубчатых колес учитывается различными коэффициентами, составляющими в результате суммарного воздействия коэффициент нагрузки К .
Коэффициент нагрузки вводится с целью компенсации неучтенных дополнительных напряжений, возникающих из-за сложного нагружения зубьев, особенностей конструкции и эксплуатации колес. Проблема выбора значения коэффициента нагрузки в зубчатых передачах – одна из сложных.

В конечном итоге при расчетах номинальные (проектные) силы F_ном или моменты Т_ном умножают на коэффициент нагрузки К , определяя тем самым расчетную нагрузку, максимально приближенную к действительной:

где F и Т – расчетные сила и момент; F_ном и Т_ном – номинальные сила и момент, соответствующие требуемой (проектной) мощности рассчитываемой машины.

Коэффициент нагрузки определяют отдельно для каждого из основных критериев работоспособности зубчатых колес. Основными критериями работоспособности для большинства зубчатых колес является усталостная контактная прочность, а также прочность зубьев при изгибе.

Коэффициент нагрузки при расчете на контактную прочность

При расчете по контактным напряжениям (на усталостную контактную прочность) коэффициент нагрузки K_Н определяется по формуле:

где К_А – коэффициент, учитывающий внешнюю динамическую нагрузку , не учтенную в циклограмме, и зависит от степени равномерности нагружения двигателя и исполнительного звена. При равномерном режиме нагружения двигателя и режиме нагружения исполнительного звена с малой неравномерностью К_А = 1,25. При задании нагрузки циклограммой моментов или типовым режимом нагружения (см. выше), в которых учтены внешние динамические нагрузки, К_А = 1.

K_Hβ – коэффициент концентрации нагрузки по ширине зубчатого венца . Этот коэффициент учитывает неравномерность распределения нагрузки по длине контактных линий зубьев в зацеплении, в том числе и изменение нагрузки по контактной линии, обусловленной изменением угла наклона зуба β .
Коэффициент K_Hβ зависит от угла перекоса зубчатых колес и от податливости сопряженных зубьев. Угол перекоса, в свою очередь, зависит от деформации валов вследствие изгиба и скручивания (для шестерен, нарезаемых на валах), а также упругих смещений опор. Очевидно, что для широкого колеса неравномерность распределения нагрузки будет большей, чем для узкого.

При расчетах учитывается способность зубьев колес прирабатываться. Приработка – это изнашивание более нагруженных участков рабочих поверхностей зубьев, после чего нагрузка распределяется по зубу более равномерно. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы K_Hβ 0 и после приработки K_Hβ . Значение коэффициента K_Hβ 0 определяют по справочным таблицам в зависимости от коэффициента ψ_bd = b₂/d₁ , схемы передачи и твердости зубьев.
Для снижения коэффициента K_Hβ неравномерности распределения нагрузки по длине контактной линии следует располагать колеса симметрично опор, увеличивать жесткость зубчатых колес, валов, опор, повышать точность изготовления, применять бочкообразные зубья и т. п.

K_Ha – коэффициент, учитывающий распределение нагрузки между зубьями . Этот коэффициент учитывает влияние ошибок окружного шага и направления зубьев от погрешностей изготовления. Значение коэффициента K_Ha определяют в зависимости от степени n_ст точности колеса по нормам плавности.

K_Hv – коэффициент, учитывающий внутреннюю динамику нагружения в зацеплении, связанную с погрешностями шагов зацепления, профилей и деформацией зубьев шестерни и колеса. На величину этого коэффициента значительное влияние оказывает неточность изготовления и монтажа передачи, а также окружная скорость колес.
Внутренняя динамическая нагрузка (присущая самой передаче) связана с ударами зубьев на входе в зацепление из-за ошибок шагов по основной окружности. Ошибки изготовления малы, и компенсируются деформациями зубьев, поэтому зацепление происходит, но с ударом (рис. 4). В зависимости от характера погрешности в шаге может иметь место кромочный (по вершине зуба – когда шаг шестерни меньше шага колеса) или срединный (в середине линии зацепления – когда шаг шестерни больше шага колеса).
Коэффициент внутренней динамической нагрузки K_Hv принимают по справочным таблицам в зависимости от степени точности, окружной скорости и твердости рабочих поверхностей.

Для определения величин перечисленных коэффициентов в справочной литературе приводятся соответствующие графики, таблицы, формулы и аппроксимирующие зависимости.

Коэффициент нагрузки при расчете на изгибную прочность

При расчете зубчатых колес по напряжениям изгиба коэффициент нагрузки определяется по формуле:

где K_Fβ – коэффициент концентрации нагрузки по ширине зубчатого венца при изгибе. При расчетах на изгиб этот коэффициент определяется по формуле:

где K_Hβ 0 – коэффициент неравномерности распределения нагрузки в начальный период работы (справочная величина).

K_Fα – коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями при изгибе. Обычно при расчетах принимают K_Fα = K_Hα .

K_Fv – коэффициент, учитывающий внутреннюю динамическую нагрузку в зацеплении при изгибе. Значение этого коэффициента принимают по справочным таблицам с учетом степени точности, окружной скорости и твердости поверхностей зубьев колес.

Допускаемые напряжения в зубчатых колесах

Во время работы зубчатой передачи зубья колес входят в зацепление поочередно и нагружаются по прерывистому отнулевому циклу. Поэтому выбор допускаемых напряжений базируется на кривых усталости, получаемых экспериментально на образцах зубчатых колес и построенных в полулогарифмических координатах σ – N (рис. 5).
С помощью кривых усталости определяют число циклов до разрушения или ресурс передачи. Кривые строят для различных видов напряжения – контактных или изгиба, для разных материалов и видов термической обработки, а также других параметров проектируемой передачи.

Допускаемые контактные напряжения для шестерни [σ]_H1 и колеса [σ]_H2 определяют по общей формуле с учетом влияния на контактную прочность долговечности (ресурса), шероховатости сопрягаемых поверхностей зубьев и окружной скорости:

где σ_{H lim} — предел контактной выносливости, определяемый по справочным таблицам в зависимости от материала зубчатого колеса и средней твердости поверхности зубьев Н_ср, равной полусумме верхнего и нижнего значений твердости.

Таблица 2. Значения σ_{H lim} , соответствующие базовому числу циклов нагружения

Источник