Конденсатор емкость которого 7 мкф включен под напряжение u 500sin314t

Линейные цепи синусоидального тока. Основные теоретические положения , страница 3

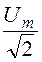
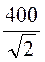
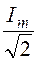
Действующие значения:U === 282 B, I === 1,061 A.

ЗАДАЧА 3.2. Цепь r, L с параметрами r = 35 Ом, L = 80 мГн питается от источника синусоидального напряжения частоты f = 50 Гц. Амплитудное значение напряжения питания U_m= 200 B, а начальная фаза ψ_u = -20°. Рас-считать мгновенное и действующее значения тока. Построить векторную диаграмму цепи. Найти активную, реактивную и полную мощности цепи. Построить треугольник мощностей.

Решение

Приведём расчётную схему цепи (рис. 3.3,а).

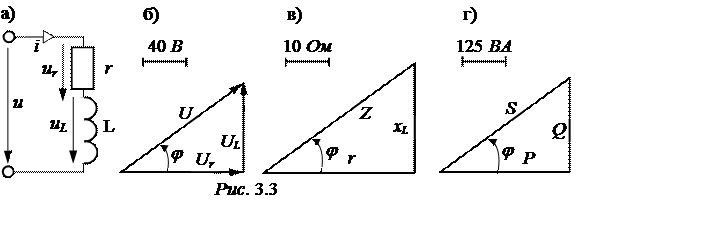Запишем мгновенное значение приложенного к цепи r, L напряжения:

Индуктивное сопротивление цепи x_L= ωL = 314×80×10 -3 = 25,12 Ом.

По второму закону Кирхгофа для контура цепи u = u_r + u_L или в век-торной форме u= u_r + u_L. На основании этого уравнения строится вектор-ная диаграмма напряжений (рис. 3.3,б).

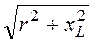
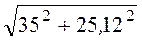
Треугольник сопротивлений цепи приведен на рис. 3.3,в. Это – прямо-угольный треугольник, из которого получаем полное сопротивление цепи Z === 43,1 Ом

и угол сдвига фаз между током и напряжением

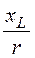
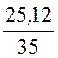
j= arctg= arctg= 35,67°.

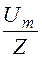
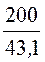
По закону Ома для амплитудных значений I_m=== 4,64 A.

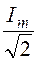
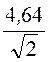
Действующее значение тока I === 3,28 A.

Действующие значения напряжений на участках:

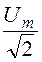
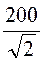
— на входе цепи (напряжение сети)u === 141,4 B.

Треугольник мощностей приведен на рис. 3.3,г.

Отметим, что на основании любого из треугольников рис. 3.3 можно рассчитать коэффициент мощности

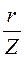
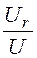
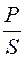
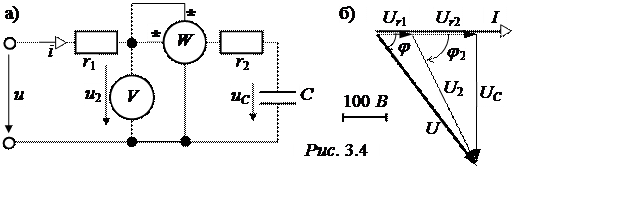cosj ===== 0,811 = cos35,67°, полученный ранее на основании треугольника сопротивлений цепи.

Рассчитать мгновенное значение напряжения сети u(t) и напряжения на конденсаторе u_С(t). Найти показания вольтметра и ваттметра. Построить векторную диаграмму цепи.

Решение

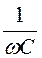
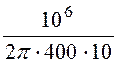
Ёмкостное сопротивление x_С=== 39,81 Ом.

Амплитудное значение напряжения на ёмкости

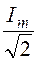
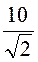
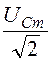
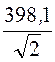
I=== 7,07 A,u_C=== 281,5 B.

Действующие значения напряжений на активных сопротивлениях

Из прямоугольного треугольника напряжений (наружный треугольник)

u=== 352 B,

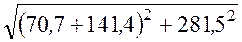
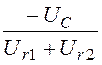
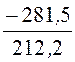
j= arctg= arctg= —53°.

Мгновенное значение напряжения сети

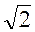
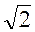
u(t)= U_m×sin(ωt+ψ_i+j) = u××sin(ωt+15°+(-53°)) = 352×sin(ωt – 38°) B.

Напряжение на конденсаторе по фазе отстаёт от тока на 90°, его мгновенное значение u_C(t)= 398,1×sin(ωt– 75°) B.

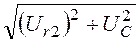
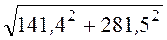
u₂ = u_W === 315 B.

Вольтметр схемы рис. 3.4,а измеряет действующее значение напряже-нияu₂ = 315 B.

Показание ваттметра: P_W = u_W ×I_W ×cos.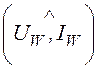

Источник

Вынужденные электрические колебания.

Расчетно-графическое задание по физике №6

Свободные колебания в идеальном колебательном контуре.

Свободные затухающие электрические колебания

Вынужденные электрические колебания.

1. Свободные колебания в идеальном колебательном контуре.

2. Свободные затухающие колебания в колебательном контуре.

3. Вынужденные электрические колебания.

5. Активное сопротивление в цепи переменного тока.

6. Емкость в цепи переменного тока.

7. Индуктивность в цепи переменного тока.

8. Закон Ома для переменного тока.

9. Работа и мощность переменного тока.

10. Колебательный контур состоит из конденсатора емкостью С = 2 нФ и катушки индуктивностью L = 1 мГн. Пренебрегая сопротивлением контура, определить, на какую волну этот контур настроен.

11. Колебательный контур содержит соленоид (длина l = 5 см, площадь поперечного сечения S₁ = 1,5 см 2 , число витков N = 500) и плоский конденсатор (расстояние между пластинами d = 1,5 мм, площадь пластинS₂ = 100 см 2 ). Определить частоту ω собственных колебаний контура.

12. Колебательный контур состоит из катушки индуктивностью L = 0,2 мГн и конденсатора с площадью пластин S = 155 см 2 , расстояние между которыми d = 1,5 мм. Зная, что контур резонирует на длину волны λ =630 м, определить диэлектрическую проницаемость среды, заполняющей пространство между пластинами конденсатора.

13. Конденсатор емкостью зарядили до напряжения U_m и замкнули на катушку индуктивностью L. Пренебрегая сопротивлением контура, определить амплитудное значение силы тока в данном колебательном контуре.

14. Колебательный контур содержит катушку с числом витков N = 100 индуктивностью L = 10 мкГн и конденсатор емкостью С = 1 нФ. Максимальное напряжение U_m на обкладках конденсатора составляет 100 В. Определить максимальный магнитный поток, пронизывающий катушку.

15. Колебательный контур состоит из катушки индуктивностью L = 10 мГн, конденсатора емкостью С = 0,1мкФ и резистора сопротивлением R = 20 Ом. Определить, через сколько полных колебаний амплитуда тока в контуре уменьшится в е раз.

16. Колебательный контур содержит катушку индуктивностью L = 25 мГн, конденсатор емкостью С = 10 мкФ и резистор сопротивлением R = 1 Ом. Начальный заряд конденсатора Q_m = 1 мКл. Определить: 1) период колебаний контура; 2) логарифмический декремент затухания колебаний; 3) уравнение зависимости изменения напряжения на обкладках конденсатора от времени.

17. Определить добротность Q колебательного контура, состоящего из катушки индуктивностью L = 2 мГн, конденсатора емкостью С= 0,2 мкФ и резистора сопротивлением R = 1 Ом.

18. Частота затухающих колебаний n в колебательном контуре с добротностью Q = 2500 равна 550 кГц. Определить время, за которое амплитуда тока в этом контуре уменьшится в 4 раза.

19. Определить период изменения синусоидального тока, если угловая частота 157 с -1 .

20. Мгновенное значение тока в цепи i=100sinωt. Найти действующее значение этого тока.

21. Определить амплитуду напряжения u=Umsin(ωt +π/2), если при t=0 U=200 В.

22. Конденсатор, емкость которого 7 мкФ, включен под напряжение u=500sin314t. Написать выражение для мгновенного значения тока и построить в масштабе графики изменения тока и напряжения.

23. К катушке с индуктивностью 50 мГн и R=0 приложено напряжение u=157sin314t. Написать выражение для мгновенного значения тока и построить в масштабе графики изменения тока и напряжения.

24. Конденсатор емкостью С=10 мкФ подключен к источнику с напряжением u=150sin500t В. Написать выражение мгновенного значения тока в цепи конденсатора и определить его действующее значение.

25. Выражение для мгновенного значения напряжения конденсатора, емкость которого 2 мкФ, имеет вид: u=169sin(100t + π/2). Определить выражение для мгновенного значения тока, протекающего через конденсатор.

26. К генератору с напряжением u=283sin500t подключен реостат с сопротивлением R=10 Ом. Написать выражение мгновенного значения тока в реостате и найти его действующее значение.

27. Мгновенные значения двух переменных токов записываются выражениями: i₁=50sin(ωt + 0º), i₂=50sin(ωt + 90º). Записать мгновенное значение результирующего тока, равного сумме двух заданных токов.

28. Емкостное сопротивление конденсатора при частоте 1000 Гц составляет 20 Ом. Определить емкость конденсатора.

29. Катушку, активным сопротивлением которой можно пренебречь, включили под синусоидальное напряжение 380 В частотой 50 Гц, и в ней установили ток 4 А. Определить индуктивность катушки.

30. К источнику с напряжением u=120sin1000t В подключена катушка, ток в которой описывается уравнением i=8sin(1000t-53º) A. Найти индуктивность и активное сопротивление катушки.

31. Определить сопротивление и проводимость конденсатора емкостью С=1 мкФ при подключении к источнику напряжения частотой 50Гц.

32. Выражения для мгновенных значений тока и напряжения имеют вид: i=14,2sin(ωt + π/2) u=169sin(ωt + π/2). Определить показания амперметра и вольтметра, а также сопротивление цепи.

33. При напряжении U=250 В в цепи, состоящей из последовательно соединенных конденсатора и резистора, ток I=5 А. Потребляемая цепью мощность — P=1 кВт. Определить активное сопротивление R и емкость конденсатора С, если частота питающего напряжения f=50 Гц. Построить векторную диаграмму.

34. Катушка индуктивности подключена к сети переменного тока с напряжением U=150 В. Ток в катушке ток I=6 А, а мощность, потребляемая катушкой, — P=540 Вт. Определить индуктивность катушки, если частота напряжения сети f=50 Гц.

35. Индуктивное сопротивление катушки в три раза больше ее активного сопротивления. При напряжении на зажимах катушки U=120 В активная мощность, расходуемая в этой катушке, P=1200 Вт. Вычислить ток и активное сопротивление катушки.

36. Ток в катушке без стального сердечника, включенной под постоянное напряжение 2,1 В, равен 0,3 А. При включении той же катушки под синусоидальное напряжение частотой 50 Гц с действующим значением 50 В ток в катушке равен 2 А. Определить параметры катушки (R и L).

37. Ток катушки, включенной в цепь с напряжением 120 В и частотой 50 Гц, равен 6 А. При этом же напряжении, но при частоте 86 Гц ток в катушке равен 4 А. Определить индуктивность катушки.

38. В катушке, присоединенной к сети с постоянным напряжением 120 В, возникает ток 20 А. В той же катушке, присоединенной к сети с переменным напряжением 220 В (частота f=50 Гц), ток составляет 28,2 А. Определить индуктивность катушки.

39. При напряжении сети U=126 В и частоте f₁=28,7 Гц ток в катушке был равен I₁=28 А. При том же напряжении, но при частоте f₂=51 Гц ток в катушке был равен I₂=21 А. Найти индуктивность катушки.

40. В цепь колебательного контура, содержащего последовательно соединенные резистор сопротивлением R = 40 Ом, катушку индуктивностью L = 0,36 Гн и конденсатор емкостью С = 28 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m = 180 В и частотой ω = 314 рад/с. Определить: 1) амплитудное значение силы тока I_mв цепи; 2) разность фаз φ колебаний силы тока и напряжения.

41. В цепь колебательного контура, содержащего катушку индуктивностью L = 0,2 Гн и активным сопротивлением R = 9,7 Ом, а также конденсатор емкостью С = 40 мкФ, подключено внешнее переменное напряжение с амплитудным значением U_m =180 В и частотой ω = 314 рад/с. Определить: 1) амплитудное значение силы тока I_m в цепи; 2) разность фаз φ между током и внешним напряжением; 3) амплитудное значение напряжения U_mL на катушке; 4) амплитудное значение напряжения U_mC на конденсаторе.

42. Последовательно соединенные резистор с сопротивлением R = 110 Ом и конденсатор подключены к внешнему переменному напряжению с амплитудным значением U_m= 110 В. Оказалось, что амплитудное значение установившегося тока в цепи I_m= 0,5 А. Определить разность фаз между током и внешним напряжением.

43. В цепь переменного тока напряжением 220 В и частотой50 Гц последовательно включены резистор сопротивлением R = 100 Ом, катушка индуктивностьюL = 0,5Гн и конденсатор емкостью С = 10 мкФ. Определить: 1) силу тока в цепи; 2) падение напряжения на активном сопротивлении; 3) падение напряжения на конденсаторе; 4) падение напряжения на катушке.

44. В цепь переменного тока частотой n = 50 Гц включена катушка длиной l = 20 см и диаметром d = 5 см, содержащая N = 500 витков медного провода площадью поперечного сечения S = 0,6 мм 2 . Определить, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм·м.

45. В цепь переменного тока частотой n = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см 2 , содержащая N = 1000 витков. Определить активное сопротивление катушки, если известно, что сдвиг фаз φ между напряжением и током составляет 30°.

46. К зажимам генератора присоединен конденсатор емкостью С = 0,15 мкФ. Определить амплитудное значение напряжения на зажимах, если амплитудное значение силы тока равно 3,3 А, а частота тока составляет 5 кГц.

47. Определить в случае переменного тока (n = 50 Гц) полное сопротивление участка цепи, состоящего из параллельно включенного конденсатора емкостью С = 10 мкФ и резистора сопротивлением R = 50 Ом.

48. В цепь переменного тока частотой n = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсатор емкостью С = 22 мкФ. Определить, какая доля напряжения, приложенного к этой цепи, приходится на падение напряжения на конденсаторе.

49. Генератор, частота которого составляет 32 кГц и амплитудное значение напряжения 120 В, включен в резонирующую цепь, емкость которой С = 1 нФ. Определить амплитудное значение напряжения на конденсаторе, если активное сопротивление цепи R = 5 Ом.

50. Активное сопротивление колебательного контура R = 0,4 Ом. Определить среднюю мощность , потребляемую колебательным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением силы тока I_m = 30 мА.

51. Колебательный контур содержит конденсатор емкостью С = 5 нФ и катушку индуктивностью L = 5 мкГн и активным сопротивлением R = 0,1Oм. Определить среднюю мощность , потребляемую колебательным контуром, при поддержании в нем незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе U_m = 10 В.

52. Колебательный контур содержит катушку индуктивностью L = 6 мкГн и конденсатор емкостью С = 1,2 нФ. Для поддержания в колебательном контуре незатухающих гармонических колебаний с амплитудным значением напряжения на конденсаторе U_m = 2 В необходимо подводить среднюю мощность = 0,2 мВт. Считая затухание колебаний в контуре достаточно малым, определить добротность данного контура.

53. В сеть переменного тока с действующим значением напряжения 120 В последовательно включены проводник с активным сопротивлением 10 Ом и катушка индуктивностью 0,1 Гн. Определить частоту n тока, если амплитудное значение силы тока в цепи равно 5 А.

Не нашли, что искали? Воспользуйтесь поиском:

Источник