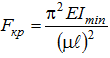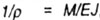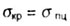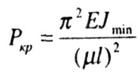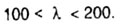Критическое напряжение с увеличением гибкости стержня уменьшается

Критическая сила. Критическое напряжение. Гибкость. Влияние способов закрепления

Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.

При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаныЭйлером.

В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:

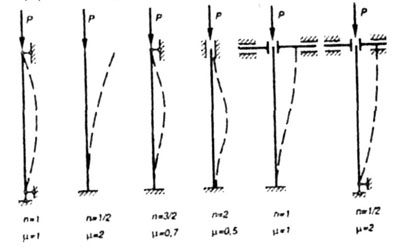
гдеI_min – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ — геометрическая длина стержня, μ – коэффициент приведенной длиныиликоэффициент приведения (зависит от способов закрепления концов стержня), Значения μприведены под соответствующей схемой закрепления стержней

Критическое напряжение вычисляется следующим образом

, где гибкость стержня ,

а радиус инерции сечения.

Введем понятие предельной гибкости.

Величинаλ_пред зависит только от вида материала:

Если у стали 3 Е=2∙10 11 Па, а σ_пц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80

Таким образом, для стержней большой гибкости λ≥λ_пред критическая сила определяется по формуле Эйлера.

В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ₀≤λ≤λ_пр,(стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.

σ_к=а-bλ, или F_кр=A(a—bλ)

где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа,b=1,14МПа.

При значениях гибкости стержня0≤λ≤λ₀ (стержни малой гибкости) потеря устойчивости не наблюдается.

Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.

Формула Эйлера и пределы ее применимости для стальных и деревянных стержней. Другие формулы для определения критической силы

Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид:

где Е — модуль продольной упругости материала стержня;

J_min — минимальный момент инерции поперечного сечения стержня.

Для стержней с другими видами закрепления формулу Эйлера записывают в виде:

где — приведенная длина стержня;

— коэффициент приведения длины.

Выражение «приведенная длина» означает, что в формуле Эйлера с помощью коэффициента все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению.

Коэффициент приведения длины иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять

На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента

Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости

в свое время полученной на основании закона Гука.

Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна

— минимальный радиус инерции (геометрическая характеристика сечения);

— минимальный момент инерции площади сечения стержня.

Значение предельной гибкости 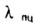получается из условия

Предельная гибкость равна

Так, для малоуглеродистой стали, если принять Е = 2×10 5 МПа,

Для повышения несущей способности конструкций в них стремятся использовать стержни возможно меньшей гибкости. Так что расчет реальных конструкций с гибкостью 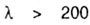практически маловероятен. Будем считать верхней границей значений гибкости реальных стержней.

Следовательно, формула Эйлера для определения критического значения сжимающей силы в виде

применима в случае, если гибкость стержня находится в пределах

Для малоуглеродистой стали этот диапазон равен

Дата добавления: 2018-04-04 ; просмотров: 3135 ; Мы поможем в написании вашей работы!

Источник

В реальных условиях при превышении предельной гибкости что может произойти?

не бывает предельной гибкости у швеллера. Бывает у элементов.

Швеллеры лучше гнуть, чем сжимать.

В случае, если используете прогоны в качестве распорок — можете посчитать на сжатие с учетом начальных несовершенств. Причем с как минимум геометрической нелинейностью, ведь изогнутый швеллер при сжатии будет сильней изгибаться.

Сараи, эстакады, этажерки и прочий металлолом

Для изгибаемого элемента? Получается, он у Вас основная колонна?

ЗЫ: «в основном всегда 150» — это просто потому что там в скаде 11 версии стоит цифра 150 и её никто не трогает, ибо не знает, что такое предельная гибкость.

ЗЗЫ: ну и, собственно, альфа — коэффициент использования на устойчивость при центральном сжатии.

Сараи, эстакады, этажерки и прочий металлолом

Источник

Критическое напряжение с увеличением гибкости стержня уменьшается

Тестовые вопросы по теме «Устойчивость сжатых стержней»

— Какую форму принимает ось сжатого стержня, если величина сжимающей силы больше критической?

— Зависит ли величина критической силы от упругих свойств материала стержня?

— Как изменится величина критической силы, если длину стержня увеличить в два раза?

2. уменьшится в четыре раза;

3. уменьшится в восемь раз.

— Как изменится величина критической силы, если шарнирные опоры концов стержня заменить опорами с жестким защемлением?

1. увеличится в четыре раза;

2. уменьшится в четыре раза.

— Если стержень теряет устойчивость, то это происходит

1. в плоскости наибольшей жёсткости;

2. в плоскости действия сил;

3. в плоскости наименьшей жёсткости.

— Формула Эйлера для определения критической силы применяется для стержней

— Кто впервые получил формулу для определения критической силы для сжатой стойки:

— Стержень теряет устойчивость:

2. в плоскости действия силы;

3. в плоскости наибольшей жесткости;

4. в плоскости наименьшей жесткости.

— Формула Эйлера для устойчивости сжатого стержня.

1. F сч = n 2 E J ρ l 2 ;

2. F сч = n 2 π 2 E J min μl 2 ;

3. F сч = n 2 E J x l 2 ;

4. F сч = n 2 π 2 E J x l 2 .

— Понятие устойчивого состояния системы.

1. Малейшие отклонения системы от положения равновесия приводят к непропорционально большим перемещениям и усилиям.

2. Это свойство системы сохранять свое состояние при внешних воздействиях.

3. Малые нарушения равновесия (отклонения от первоначального положения) вызывают малые изменения в напряженно-деформированном состоянии системы.

4. Это состояние, при котором система может сохранять заданную форму или потерять ее при любом малом внешнем воздействии.

1. Значение силы, при которой система может переходить из первоначального положения в новое деформированное, называется критическим.

2. Наибольшее значение силы, при котором происходит разрушение системы, называется критическим.

3. Минимальное значение силы, при котором система может переходить из первоначального положения в новое деформированное, называется критическим.

4. Это сила, при которой система теряет устойчивость.

— Пределы применимости формулы Эйлера для материала типа стали.

1. λ ≥100 ;

2. λ

3. 40≤ λ ≤100 ;

4. 0≤ λ ≤100 .

1. σ кр = a — bλ ;

2. σ кр = N кр A ;

3. σ кр = π 2 E λ 2 ;

4. σ кр ≤ σ adm .

— Что понимают под «устойчивостью сжатых стержней»?

1. отсутствие разрушения при сжатии;

2. отсутствие опрокидывания;

3. способность сохранять первоначальную форму равновесия;

4. способность восстанавливать исходную форму равновесия.

— Что такое «критическая сила»?

1. максимально сжимающая сила, при которой стержень сохраняет прочность;

2. минимальная сжимающая сила, при которой стержень теряет устойчивость;

3. максимальная сила, при которой стержень сохраняет устойчивость;

4. минимальная сила, при которой в стержне появляются пластические деформации.

— Выбрать правильную запись условия устойчивости сжатого стержня

1. σ сж ≤ σ m S ;

2. σ сж a — bλ ;

3. σ сж ≤ σ кр S y ;

4. σ сж ≤ F сж A .

— Выбрать правильную запись условия устойчивости

1. F сж F кр ;

2. F сж ≤ F кр S y ;

3. F сж = σ сж A ;

4. F сж ≤ σ кр A .

1. силы сжатия, при которых наступает предел текучести;

2. силы, при которых сжатый стержень теряет устойчивость, упругое равновесие;

3. силы, при которых стержень разрушается.

— Потеря устойчивости происходит в результате продольного изгиба относительно главной оси сечения, относительно которой осевой момент инерции.

3. момент сопротивления максимальный.

— Критические напряжения Эйлера должны быть:

3. при значениях λ ≥100 .

— Зависимость Ясинского применяется, если:

1. σ кр = σ Т ;

2. 100≥ λ ≥40 ;

3. при i min = J min A .

— Условие устойчивости сжатого стержня:

1. σ кр = F кр A = φ σ ;

2. σ кр > σ Т ;

3. σ y = φ σ .

— Формула Эйлера при расчете устойчивости сжатого стержня:

1. F кр = π 2 E J min μl 2 ;

2. F кр = π 2 E J max μl 2 ;

3. F кр = π 2 E A i min .

— Пределы применимости формулы Эйлера

1. σ кр = σ T ;

2. σ кр = a — bλ ;

3. σ кр = π 2 E .

— Из приведенных характеристик материала выбрать характеристику, используемую при расчете на устойчивость

— Критические напряжения при потере устойчивости больше предела текучести.

3. зависят от скорости приложения осевой нагрузки.

— Коэффициент приведенной длины стержня при вычислении критической силы по формуле Эйлера зависит от .

1. величины приложенной силы

2. способа закрепления стержня

4. формы поперечного сечения стержня

— Вывод формулы Эйлера для критической силы сжатого стержня основан на предположении, что под действием сжимающей силы, равной критической силе, стержень изогнется, при этом.

1. напряжения достигают предела текучести

2. напряжения превышают предел текучести

3. в стержне возникают пластические деформации

4. деформации подчиняются закону Гука

— Признаком потери устойчивости сжатого стержня является.

1. увеличение напряжения до предела текучести

2. внезапной смены прямолинейной формы равновесия на криволинейную

3. увеличение напряжения в поперечном сечении до предела пропорциональности

4. увеличение напряжения до предела упругости

— Формула Эйлера для критической силы имеет вид.

1. P кр = σA , где σ нормальное напряжение в поперечном сечении стержня, А – площадь сечения

2. P кр = π 2 E I max l 2 , где l – длина стержня

3. P кр = EAε , где ε — продольная деформация

4. P кр = π 2 E I max μl 2 , где E – модуль упругости, I min — минимальный осевой момент инерции сечения стержня, μl — приведенная длина с тержня

— Для определения критической нагрузки за пределом пропорциональности используется формула.

3. нормальных напряжений при изгибе

4. нормальных напряжений при растяжении-сжатии

— Какова зависимость между критическим напряжением и гибкостью в формуле Ясинского (для балки из любого материала)?

— Во сколько раз увеличится критическое напряжение, если длину стержня уменьшить вдвое? Применима формула Эйлера.

— Чему равен минимальный радиус инерции прямоугольного сечения h > b ?

— По какой формуле определяется минимальный радиус инерции?

1. I min A ;

2. I min A ;

3. I min S z ;

4. I min λ .

— От каких упругих постоянных материала зависит критическое напряжение при расчетах на устойчивость?

— Во сколько раз увеличится F _cr , если l уменьшить вдвое?

— Какова зависимость между критическим напряжением и гибкостью стержня по формуле Эйлера?

— По какой формуле определяется критическое напряжение при расчете на устойчивость?

1. P A ;

2. π 2 E λ 2 ;

3. π 2 E ( μ l ) 2 ;

4. P cr A ;

5. π 2 E I min ( μ l ) 2 .

— Во сколько раз увеличится гибкость стержня, если минимальный радиус инерции уменьшить вдвое?

— Укажите формулу Эйлера для определения критического напряжения

1. π 2 E I min λ 2 ;

2. π 2 E λ 2 ;

3. π 2 E I min ( μl ) 2 .

— Как определяется гибкость стержня?

1. μ i min l ;

2. i min μl ;

3. μl i min .

— Во сколько раз увеличится σ _cr по формуле Эйлера, если диаметр и длина круглого стержня удвоятся?

— Укажите пределы применимости формулы Эйлера для стальных балок

1. 80≥ λ ≥100 ;

2. λ ≥100 ;

3. λ .

— По какой из приведенных формул определяется критическое напряжение в стальной балке из стали Ст3, если её гибкость равна 115?

1. a — bλ + c λ 2 ;

2. π 2 E ( μl ) 2 ;

3. π 2 E I min ( μl ) 2 ;

4. a — bλ ;

5. π 2 E λ 2 .

— Какова зависимость между критическим напряжением и гибкостью в формуле Ясинского?

— Во сколько раз увеличится критическая сила, если минимальный момент инерции сечения увеличить в 2 раза?

— Укажите пределы применимости формулы Эйлера для чугунных балок

1. λ ≥100 ;

2. λ ≥90 ;

3. λ ;

4. λ ≥80 ;

5. λ .

— С каким запасом устойчивости работает балка, если на неё действует нагрузка P =15 г., площадь поперечного сечения балки 20 см 2 , критическое напряжение равно 1600 кг/см 2 ?

— Укажите пределы применяемости формулы Ясинского для стальных балок

1. 80≥ λ ≥40 ;

2. 80≥ λ ≥20 ;

3. 80≥ λ ≥30 ;

4. 100≥ λ ≥80 ;

5. 100≥ λ ≥40 .

— Укажите объединенную расчетную формулу устойчивости

1. a — bλ + c λ 2 ;

2. π 2 E λ 2 ;

3. P F ≤ φ σ .

— Чему равна допускаемая продольная сила, если площадь сечения равна 15 см 2 , φ =0,76 и допускаемое напряжение на сжатие – 1600 кг/см 2 ?

— При каком значении напряжений нельзя применять формулу Эйлера?

1. σ σ T ;

2. σ σ пц ;

3. σ > σ b ;

4. σ > σ T ;

5. σ > σ пц .

— Чему равна гибкость квадратного стержня длиной 1 м., если оба его конца защемлены ( a = 5 см., l = 1 м)?

— Относительно какой оси радиус инерции сечения является минимальным?

— Чему равно допускаемое напряжение на устойчивость, если основное допускаемое напряжение на сжатие равно 1600 кг/см 2 , а коэффициент продольной устойчивости – 0,76?

— Какой коэффициент приведения длины соответствует приведённой схеме?

1. μ =1 ;

2. μ =2 ;

3. μ =0,5 ;

4. μ =0,7 .

— Как записывается формула для определения критической силы данного стержня?

1. F = π 2 E J min l 2 ;

2. F = π 2 E J max μl 2 ;

3. F = E J max l 2 ;

4. F = E J min μl 2 .

— При сжатии упругого стержня, показанного на рисунке, силой P ≥ P _кр форма потери устойчивости стержня имеет вид.

1.

2.

3.

4.

— Чему равен коэффициент приведения длины?

— Чему равен коэффициент приведения длины?

— Можно ли применить формулу Ясинского для определения критического напряжения в стальном стержне из стали Ст3 длиною 2 м с радиусом инерции i _min = 3 см?

— Во сколько раз увеличится критическое напряжение, если обе стороны “ a ” и длину l стержня квадратного сечения удвоить?

— Чему равен радиус инерции относительно оси Z сечения, состоящего из двух швеллеров, если радиус инерции одного швеллера равен i _z ?

— Чему равно критическое напряжение стального стержня, если l = 3 м., i _min = 2 см?

— Какой стержень является менее устойчивым?

3. устойчивость обоих стержней одинаковая.

— У какого стержня критическая сила больше?

3. у обоих стержней критические силы равны.

— Какой момент инерции нужно подставить в формулу Эйлера для вычисления критической силы

2. I x 0 ;

3. I y 0 ;

4. I y .

— Чему равна приведенная длина стержня?

— Чему равна гибкость стержня, если l = 3 м, I _min = 25 см 2 , A = 2 c м 2 ?

— Во сколько радиус инерции верхнего составного сечения больше, чем у нижнего (относительно оси x )?

— Чему равен коэффициент приведения длины?

— Можно ли применить формулу Эйлера для расчета стальной балки из стали Ст3 длиной l =1 м, если площадь е сечения равна A = 9 см 2 , I _min = 6,75 см 4 ?

— Чему равна приведенная длина стержня?

— Чему равна гибкость стержня, если l = 3 м., I _min = 120 см 4 , A = 45 см 2 ?

— Во сколько раз увеличится критическое напряжение, если одну сторону стержня квадратного сечения удвоить?

— У какого стержня критическая сила больше?

3. у обоих стержней одинакова величина критической силы.

— Относительно какой оси стержень потеряет устойчивость?

— Устойчив ли стержень, представленный на схеме. Действующая сжимающая сила 10 кН, запас устойчивости 4, материал – сталь Е = 2 ∙ 10 5 МПа

— Устойчив ли стержень (см. схему)? Действующая сила 134 кН, материал сталь, Е = 2 ∙ 10 5 МПа, сечение – двутавр № 18, запас устойчивости 3. Применима формула Эйлера

4. расчет на устойчивость не требуется.

— Рассчитать F _кр для стержня, представленного на схеме. Сечение – двутавр № 20, материал сталь E = 2 ∙ 10 5 МПа

— Определить приведенную длину стержня для расчета на устойчивость, если l= 3 м

— От каких параметров сжатого стержня (см. приведенный график) зависит величина предельной гибкости?

— Как изменится F _кр при замене поперечного сечения: вместо двутавра №16 используется двутавр № 20 (при прочих равных условиях)?

— Как изменится критическая сила при замене прямоугольного сечения на сечение в форме двутавра ?

— Как изменится гибкость стержня при замене схемы крепления концов с варианта А на вариант Б?

— По какой из приведенных формул следует рассчитывать стержень, изображенный на схеме, если материал — сталь, а сечение – двутавр № 20?

1. F кр = π 2 E J min μ l 2 ;

2. F кр = a — b λ A ;

3. F кр = σ T A .

4. расчет на устойчивость не проводится.

— Определить допускаемую нагрузку для стержня представленного на схеме, если запас устойчивости трехкратный? Материал сталь Е = 2 ∙ 10 5 МПа, а сечение – двутавр № 20.

— Рассчитать гибкость стержня круглого поперечного сечения, если его диаметр 60 мм, длина 2,4 м, стержень шарнирно закреплен с обоих концов

— По какой из приведенных формул следует рассчитывать на устойчивость стержень, представленный на схеме, если материал стержня сталь, предельная гибкость для которой 96?

1. F кр = π 2 E J min μ l 2 ;

2. F кр = a — b λ A ;

3. F кр = σ сж A ;

4. F кр = σ T A .

— Определить допускаемую нагрузку для стойки. Материал – сталь Е = 2 ∙ 10 5 МПа, поперечное сечение – швеллер № 16, запас устойчивости 4.

— Как изменится F _кр при замене первого способа крепления стержня на второй?

— Определить величину гибкости для стержня. Сечение – швеллер № 16, длина l = 5 м

— По какой из формул следует рассчитывать устойчивость стержня на участке 2?

1. π 2 E J min μ l 2 ;

2. a — b λ A ;

3. σ сж A .

4. подходящая формула не приведена.

— Чему равно критическое напряжение для круглого стержня, если известно, что F _сж = 8кН; [ F _у] =12 кН; F _кр =24 кН; диаметр стержня 50 мм?

— Как изменится критическая сила, если длину стойки увеличить в 3 раза?

— Рассчитать гибкость стального стержня. Поперечное сечение – двутавр № 18.

— По какой из формул следует рассчитывать устойчивость стержня на участке 3?

1. σ сж ≤ σ T ;

2. σ сж ≤ a — b λ ;

3. σ сж ≤ π 2 E λ 2 ;

4. σ сж = π 2 E J min μλ 2 А .

— Если несколько одинаковых стоек, имеющих кольцевое поперечное сечение ( ∅ 52/60), жестко закреплены как в основании, так и в массивной недеформируемой плите, которая подвергается нагрузке F , то гибкость (λ) каждой из них:

— Стальной стержень сжат силой F =180 кН. Опорные закрепления в обеих главных плоскостях инерции одинаковы. На сколько процентов можно максимально увеличить силу F , чтобы еще сохранилась устойчивость стержня? Принять нормативный коэффициент запаса устойчивости [ n _y ] =2 и модуль продольной упругости E =2 ∙ 10 11 Па.

— Если участок трубопровода жестко закрепить в опорах А и В, то его гибкость λ в связи с расчетом на устойчивость равна:

— Стальной стержень, имеющий двутавровое поперечное сечение, сжат силой F . Опоры: в плоскости чертежа – две заделки, из плоскости – заделка внизу и свободный конец наверху. Для какого из указанных ниже профилей можно создать стержень, равноустойчивый в обеих главных плоскостях инерции?

— Стержень, имеющий прямоугольное поперечное сечение ( bxh ), сжат силой F . Опоры: в плоскости чертежа – две заделки, из плоскости – заделка внизу и свободный конец наверху. Стержень будет равноустойчивым в обеих главных плоскостях инерции, если соотношение размеров h / b равно:

— Если охладить третий стержень, то какой из трех стержней, удерживающих в равновесии недеформированный брус CD , потеряет устойчивость?

— Сила F сжимает деревянную стойку, поперечное сечение которой – квадрат со стороной a =0,2 м. Если предельная гибкость λ_{пр .}=110, a рекомендуемая – не более λ_{ма x} =200, то максимально допустимая высота стойки в м. равна:

— Стержень длиной l = 2 м с промежуточным шарнирным закреплением сжат силой Р. Зависимость критического напряжения от гибкости λ для стали Ст.3 приведена на рисунке.

Поперечное сечение стержня представляет собой швеллер №10, радиусы инерции которого i _x =3,99 см, i _y =1,37 см. Критическое напряжение для стержня равно.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник