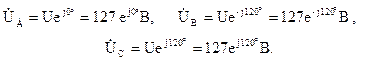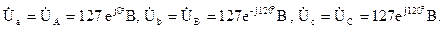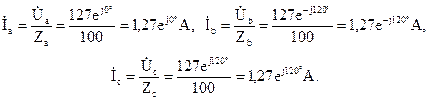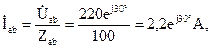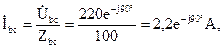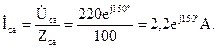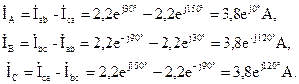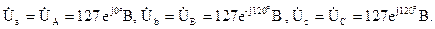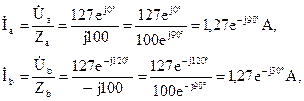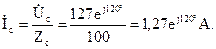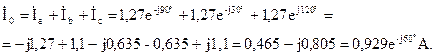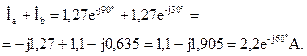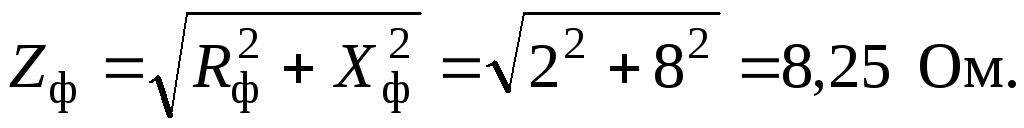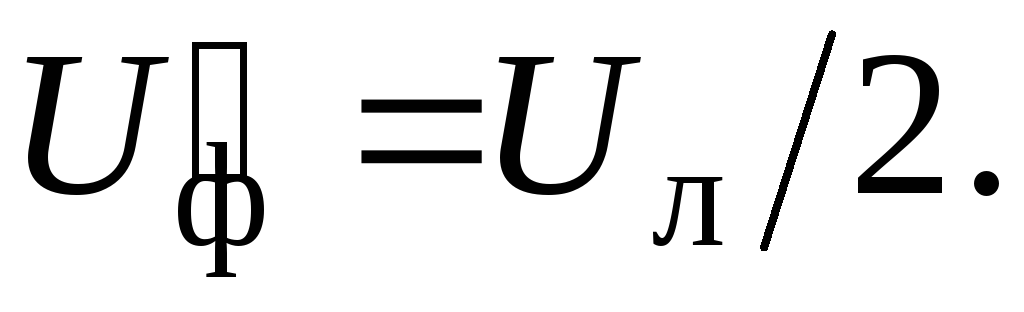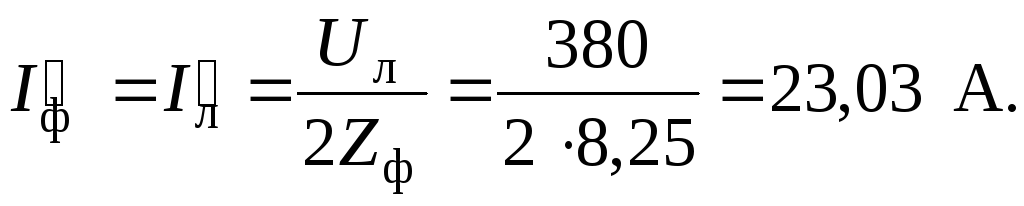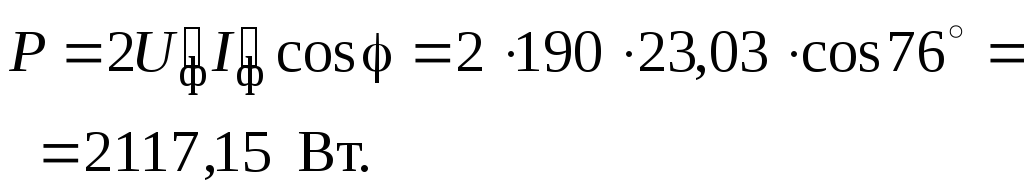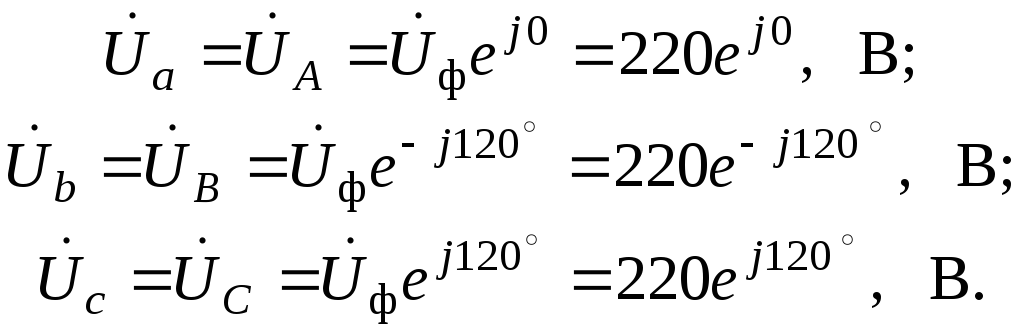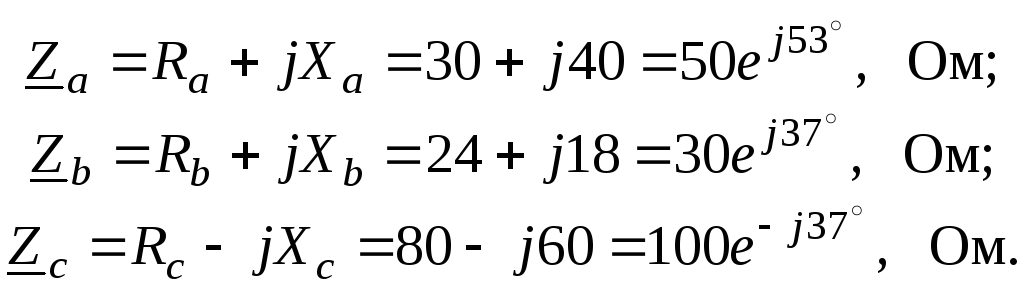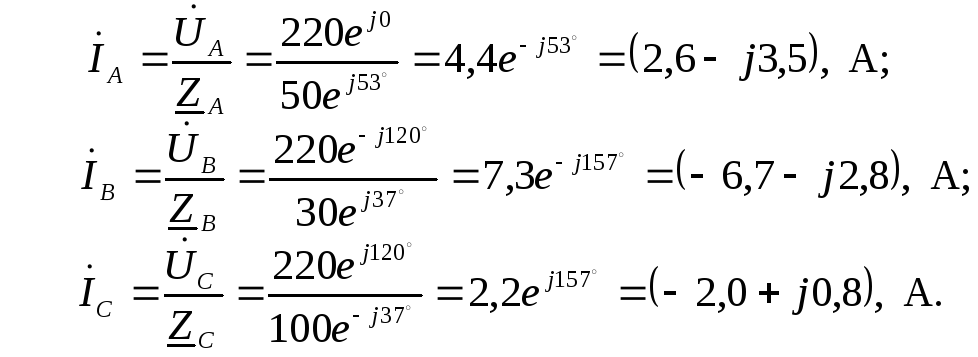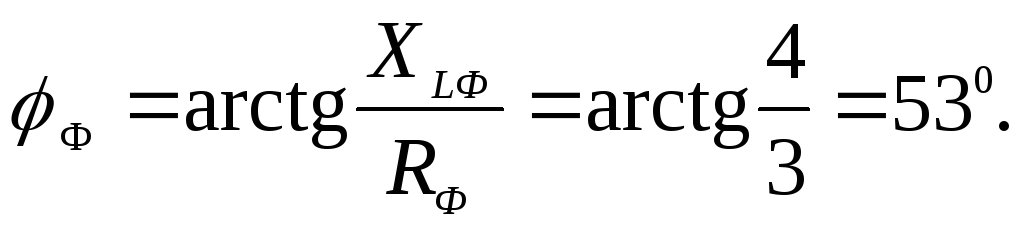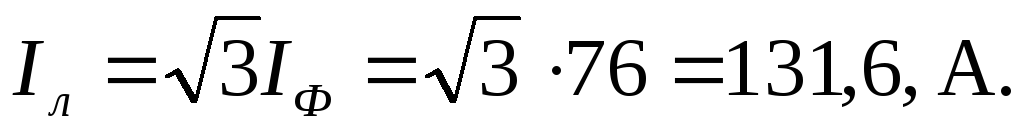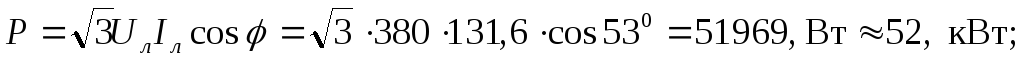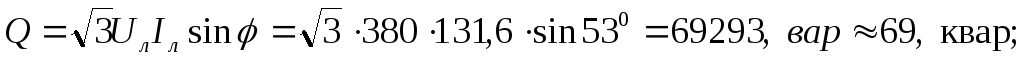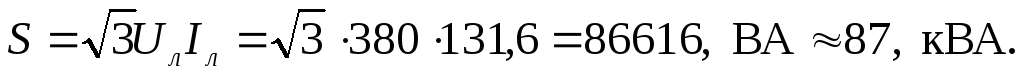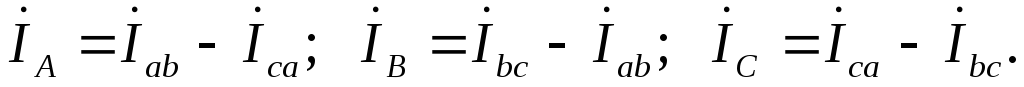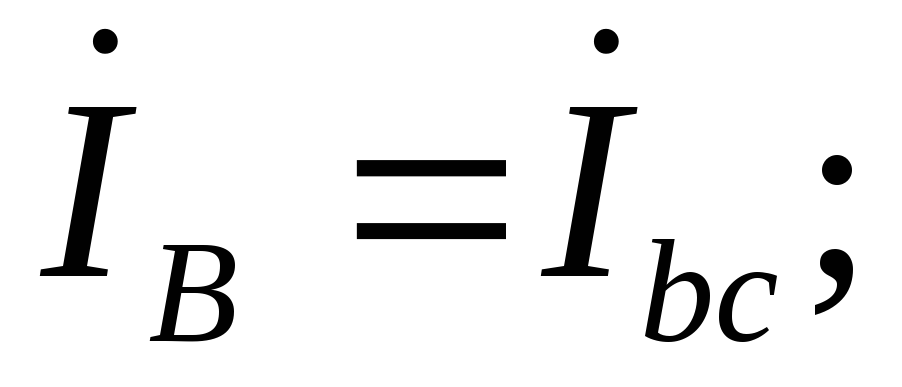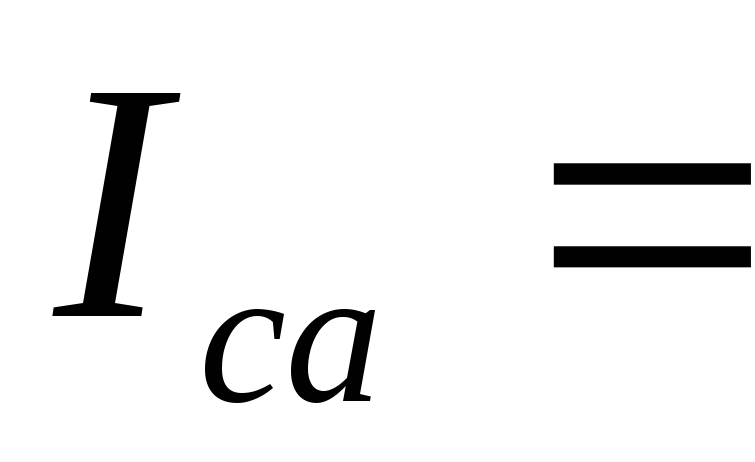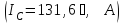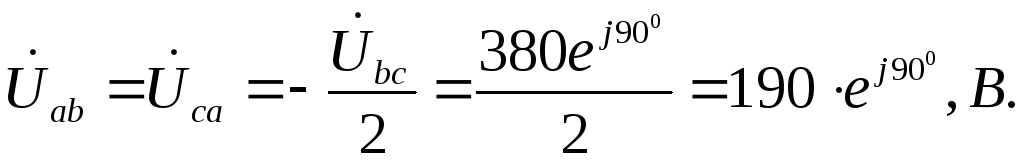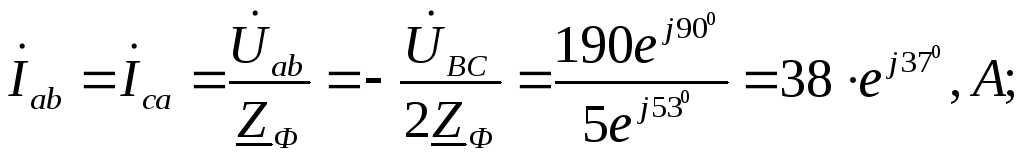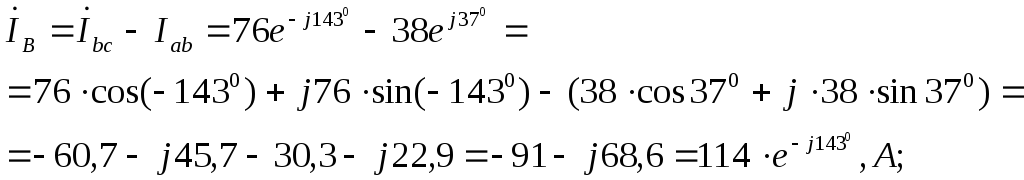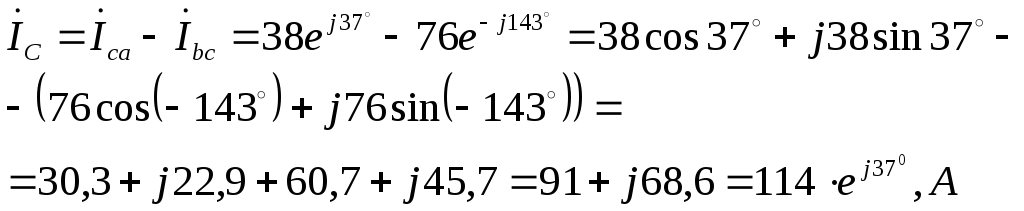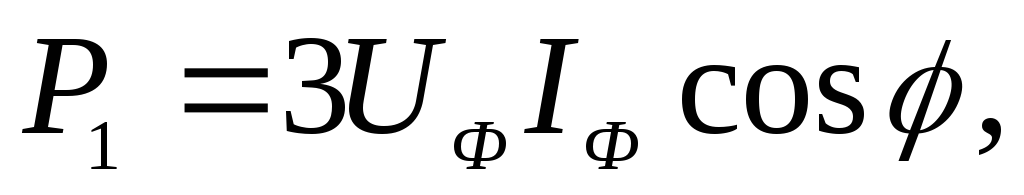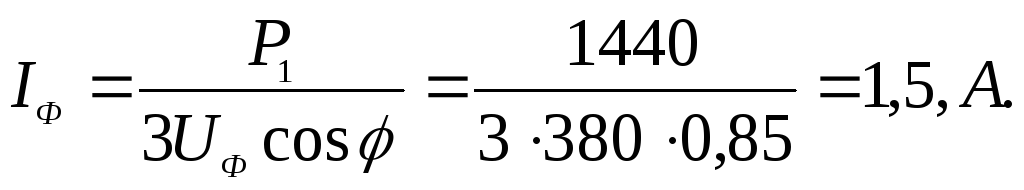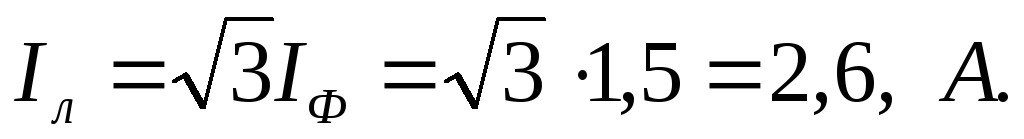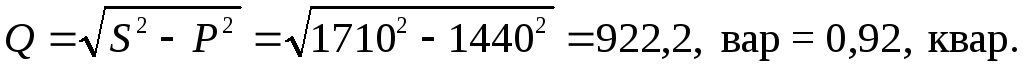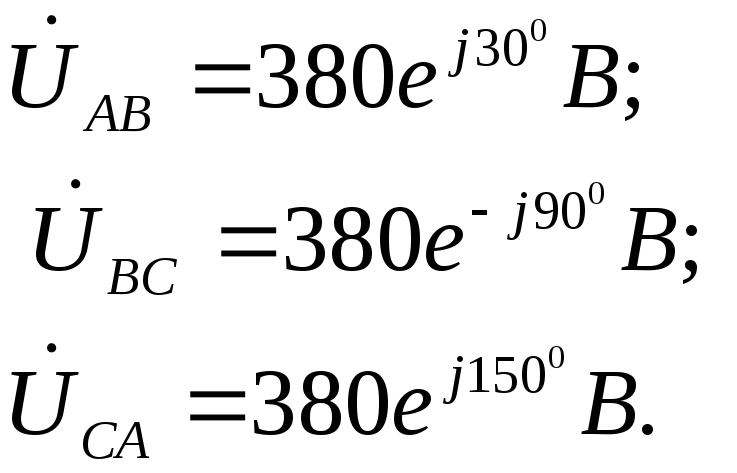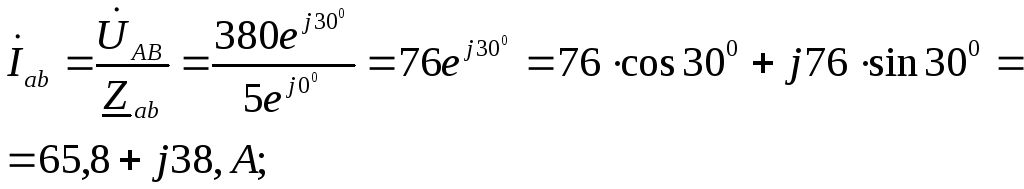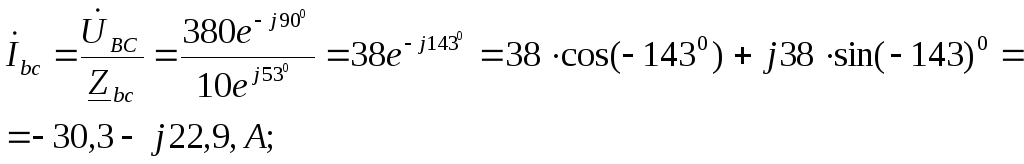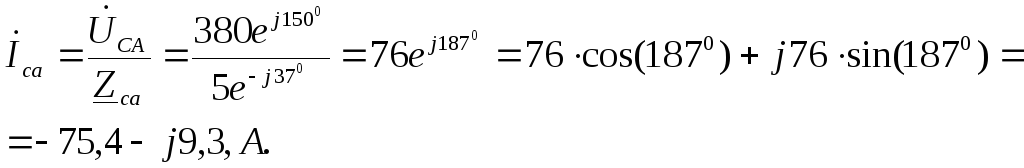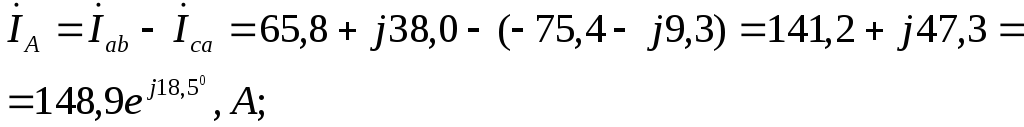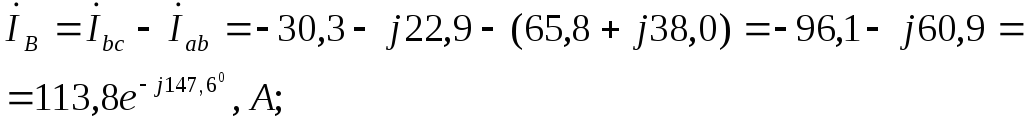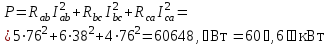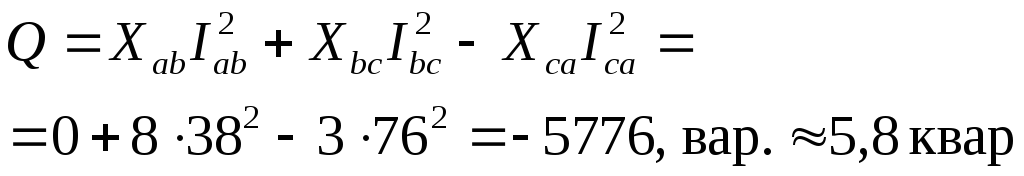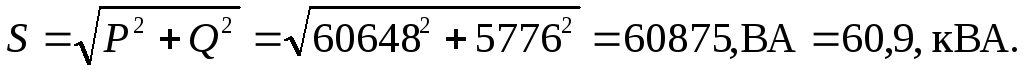Линейное напряжение решение задач

Примеры решения задач. 3.2.1Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда при наличии и отсутствии нулевого провода (рис

3.2.1Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда при наличии и отсутствии нулевого провода (рис. 3.10). Питание осуществляется от источника с линейным напряжением U_Л = 220В, сопротивления фаз нагрузки одинаковы и равны Z_а = Z_b = Z_c = Z_Ф = R = 100 Ом.

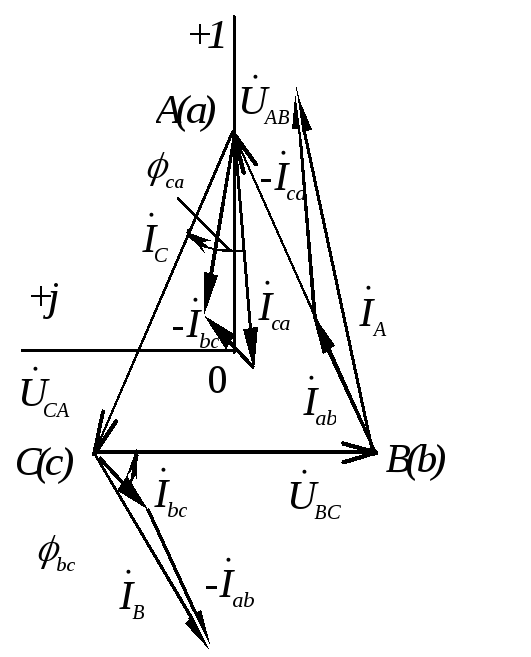
Построить векторную диаграмму рассчитанных токов и напряжений.

При симметричной нагрузке расчет токов и напряжений для схемы с нулевым проводом и без нулевого провода выполняется одинаково, так как в трехпроводной схеме напряжение смещения нейтрали равно нулю 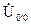= 0 и, следовательно, фазные напряжения приемников равны фазным напряжениям генератора, а в четырехпроводной схеме ток нулевого провода отсутствует I₀ = 0.

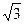
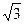
Фазные напряжения генератора U_фг = U_Л/ = 220/ = 127 В.

Фазные напряжения генератора в комплексной форме записи:

Фазные напряжения приемников равны соответствующим фазным напряжениям генератора:

Фазные токи приемников определим по закону Ома:

Построим векторную диаграмму токов и напряжений для режима симметричной нагрузки (рис. 3.11).

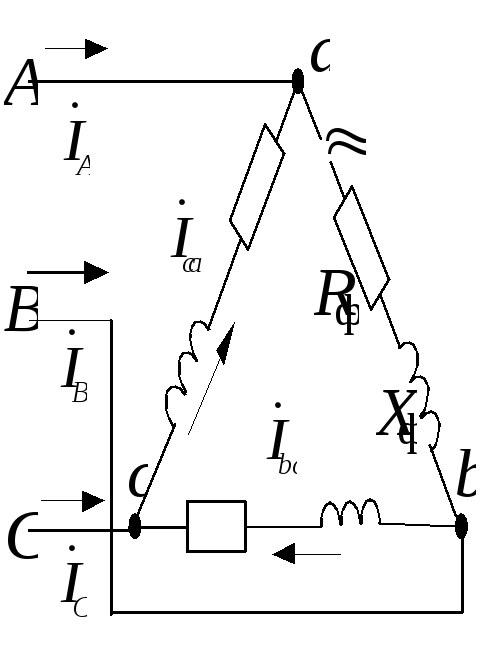
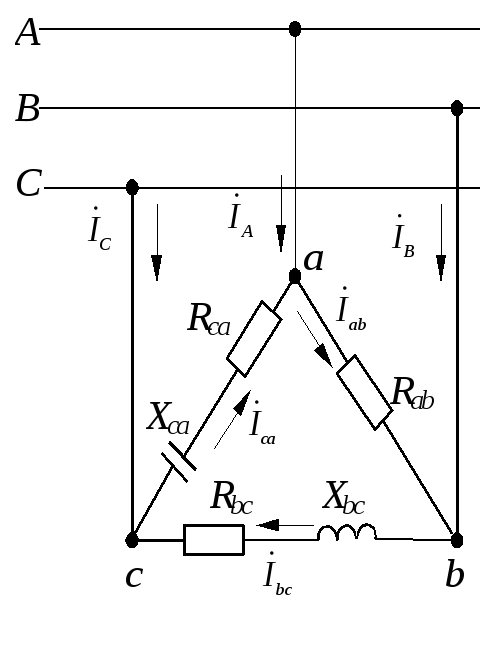
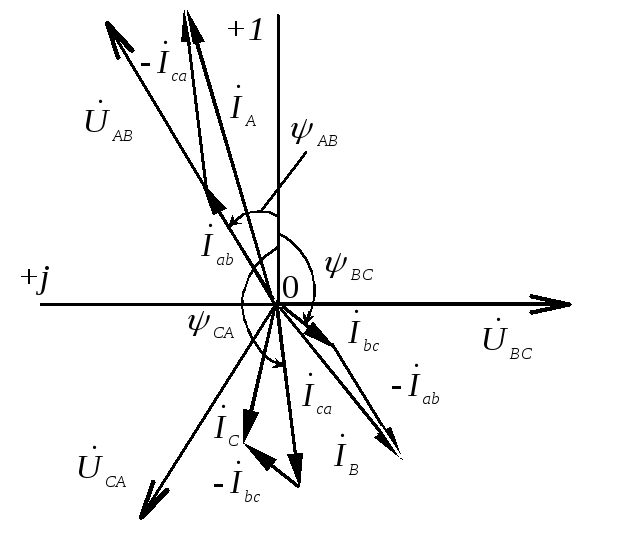
3.2.2Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме треугольник (рис. 3.12), питающейся от источника с линейным напряжением U_Л = 220В, сопротивления фаз нагрузки одинаковы и равны Z_аb= Z_bc = Z_ca = Z_Ф = R = 100 Ом.

Построить векторную диаграмму рассчитанных токов и напряжений.

Фазные напряжения приемников, при соединении фаз нагрузки треугольником, равны линейным напряжениям генератора, поэтому фазные токи легко определяются по закону Ома:

Как видно по расчетам, все токи получились одинаковые по модулю и сдвинуты друг относительно друга по фазе на 120°.

Линейные токи определяем по уравнениям, составленным с помощью первого закона Кирхгофа:

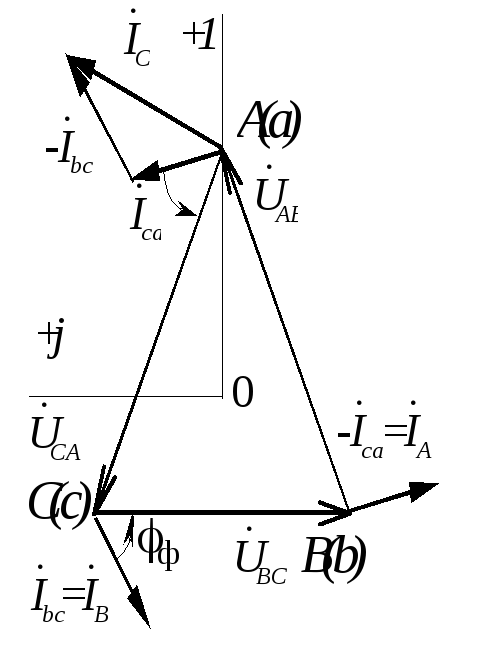
Линейные токи при симметричной нагрузке также получаются одинаковыми по модулю и сдвинутыми друг относительно друга по фазе на 120°. Это хорошо видно на векторной диаграмме токов и напряжений (рис. 3.13).

Линейные и фазные токи приемника при симметричной нагрузке связаны соотношением: I_Л = 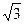I_Ф.

3.2.3Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда с нулевым проводом (рис. 3.14). Питание осуществляется от источника с линейным напряжением U_Л = 220В, сопротивления фаз нагрузки: Z_а = jX_L=j100 Ом, Z_b = –jX_c= –j100 Ом, Z_c = R = 100 Ом. Построить векторную диаграмму токов и напряжений.

В схеме с нулевым проводом фазные напряжения приемника равны соответствующим фазным напряжениям генератора:

Фазные токи приемников определим по закону Ома:

Рис. 3.15

Ток в нулевом проводе определяется с помощью первого закона Кирхгофа:

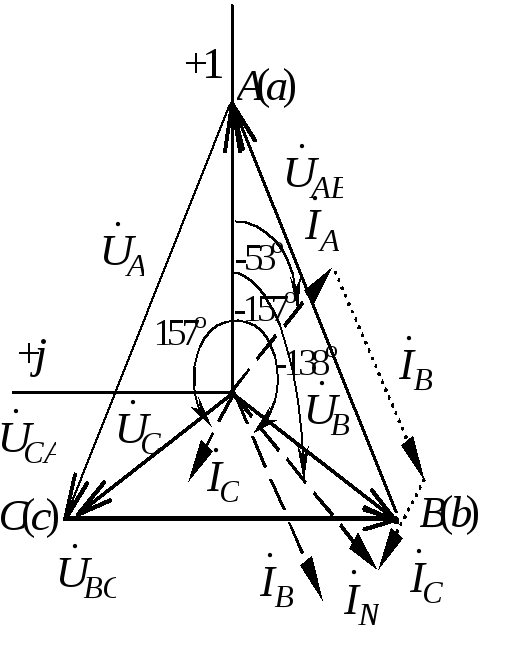
Построим векторную диаграмму токов и напряжений (рис. 3.15).

3.2.4По данным задачи 3.2.3. рассчитать значение активного сопротивления резистора R, включенного в фазу с нагрузки, при котором ток нулевого провода будет равен нулю.

Как видно по векторной диаграмме (рис. 3.15), ток нулевого провода будет отсутствовать в том случае, если действующее значение тока фазы с будет равно сумме токов фаз a и b. Сумма фазных токов:

Действующее значение тока фазы с: 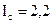А.

Сопротивление резистора определим по закону Ома:

Ом.

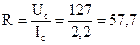
Источник

Трехфазные электрические цепи

Содержание главы

Примеры решений задач

Данные примеры задач, относятся к предмету «Электротехника».

Задача #4511

К источнику трехфазной сети с линейным напряжением U_л = 380 В и частотой f = 50 Гц подключена равномерная нагрузка, соединенная по схеме «звезда», с полным сопротивлением в фазе Z = 90 Ом и индуктивностью L = 180 мГн. Определить активную, реактивную и полную мощности, коэффициент мощности, действующее значения линейного тока. Построить векторную диаграмму токов и напряжений.

I ф = U ф Z = 220 90 = 2,45 А

Активное сопротивление в фазе:

R = Z 2 — X L 2 = 90 2 — 56,5 2 = 70 О м

Коэффициент мощности катушки:

Мощность, потребляемая нагрузкой:

P = 3 U ф I ф cos ⁡ φ = 3 × 220 × 2,45 × 0,778 = 1260 В т = 1,26 к В т

Q = 3 U ф I ф sin ⁡ φ = 3 × 220 × 2,45 × 0,628 = 1010 В т ≈ 1 к В т

S = 3 U ф I ф = 3 × 220 × 2,45 = 1620 В т = 1,62 к В т

Векторная диаграмма токов и напряжений представлена на рисунке.

Ответ: P = 1,26 кВт; Q = 1 кВт; S = 1,62 кВт; cos φ = 0,778; I_л = 2,45 А.

Задача #4512

К четырех проводной трехфазной сети с действующим значением линейного напряжения 220 В подключена неравномерная активная нагрузка с потребляемой мощностью в фазах P_A = 3 кВт, P_B = 1, 8 кВт, P_C = 0,6 кВт. Определить действующее значение тока в нейтральном проводе.

I A = P A U ф = 3000 127 = 23,6 А

I B = P B U ф = 1800 127 = 14,2 А

I C = P C U ф = 600 127 = 4,72 А

Ток в нейтральном проводе определяем из векторной диаграммы (см. рисунок) как сумму векторов фазных токов:

I N ˙ = I A ˙ + I B ˙ + I C ˙ = 16 А

Задача #4513

К трехфазной четырехпроводной сети с действующим значением линейного напряжения U_л = 380 В и частотой f = 50 Гц подключен приемник энергии, соединенный по схеме «звезда». В фазу A включена катушка с индуктивностью L = 0,18 Гн и активным сопротивлением R_A = 80 Ом, в фазу B – резистор сопротивлением R_B = 69 Ом, в фазу C – конденсатор емкостью C = 30 мкФ с последовательно соединенным резистором сопротивлением R_C = 40 Ом. Определить действующие значения линейных и фазовых токов, полную потребляемою нагрузкой мощность.

Z A = R А 2 + X L 2 = R А 2 + 2 π f L 2 = 80 2 + 2 π × 50 × 0,18 2 = 98 О м

Z C = R C 2 + X C 2 = R А 2 + 1 2 π f C 2 = 80 2 + 1 2 π × 50 × 30 × 10 — 6 2 = 110 О м

I A = U ф Z A = 220 98 = 2,25 А

I B = U ф Z B = 220 69 = 3,2 А

I C = U ф Z C = 220 110 = 2 А

P A = I A 2 R A = 2,25 2 × 80 = 405 В т

P B = I B 2 R B = 3,2 2 × 69 = 704 В т

P C = I C 2 R C = 2 2 × 40 = 160 В т

P н = P A + P B + P C = 405 + 704 + 160 = 1269 В т

Q A = I A 2 X L = 2,25 2 × 56,5 = 285 в а р

Q C = — I C 2 X C = — 2 2 × 106 = — 425 в а р

Q н = Q A + Q C = 285 + — 425 = — 140 в а р

S = P н 2 + Q н 2 = 1269 2 + 140 2 = 1280 В × А = 1,28 к В × А

Ответ: I_A = 2,25 А; I_B = 3,2 А; I_C = 2 А; S = 1,28 кВ × А.

Задача #4514

К трехфазному генератору, обмотки которого соединены по схеме «звезда», подключена равномерная нагрузка, соединенная по той же схеме, через линию, обладающую активным сопротивлением R = 2 Ом и индуктивностью L = 16 мГн. Полное сопротивление нагрузки в каждой фазе Z_н = 80 Ом (конденсатор емкостью C = 53 мкФ с последовательно включенным резистором). Определить действующее значение напряжения в нагрузке, если линейное напряжение генератора U_л = 380 В при частоте f = 50 Гц. Построить векторную диаграмму токов и напряжений.

Фазное напряжение генератора

Активное сопротивление нагрузки:

R н = Z н 2 — X C 2 = Z н 2 — 10 6 2 π f C 2 = 80 2 — 10 6 2 × 3,14 × 50 × 53 2 = 16,7 О м

Реактивное сопротивление нагрузки и линии:

X н = — 10 6 2 π f C = — 10 6 2 × 3,14 × 50 × 53 = — 60 О м

X л = 2 π f L = 2 × 3,14 × 50 × 16 × 10 — 3 = 5 О м

I л = U ф R н + R л 2 + X н + X л 2 = 220 16,7 + 2 2 + — 60 + 5 2 = 3,8 А

Для построения векторной диаграммы (см. рисунок) определяем угол сдвига по фазе между напряжением на зажимах генератора и током в линии:

φ = atan ⁡ X н + X л R н + R л = atan ⁡ — 55 18,7 = — 71 °

Найдем падение напряжения на активном и индуктивном сопротивлениях линии соответственно:

Δ U R л = I л R л = 3,8 × 2 = 7,6 В

Δ U X л = I л X л = 3,8 × 5 = 19 В

Падение напряжения на нагрузке:

U R н = I л R н = 3,8 × 16,7 = 63,6 В

U X н = I л R н = 3,8 × 60 = 228 В

Задача #4515

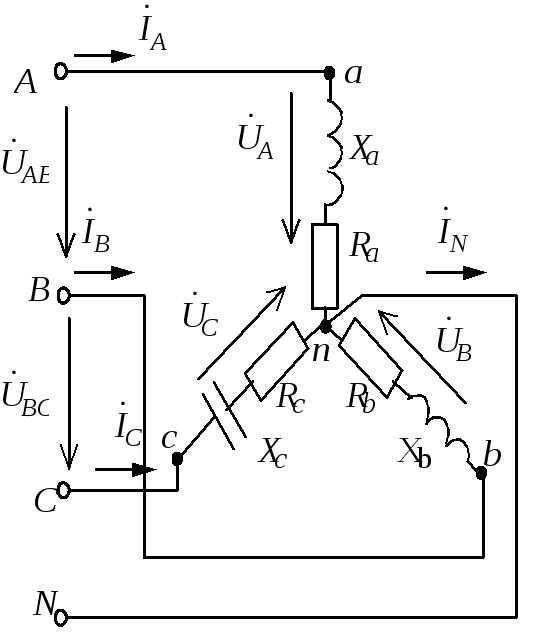
К трехфазной сети с нулевым проводом подключена несимметричная нагрузка фазы которой характеризуются следующими параметрами: для фазы A R_A = 0,8 Ом и X_LA = 1,2 Ом; для фазы В R_B = 0,4 Ом и Х_CB = -2 Ом; для фазы С R_C = 1 Ом и X_LC = 1,8 Ом. Определить фазные и линейные токи, ток нулевого провода и коэффициенты мощности каждой фазы при соединении фаз нагрузки звездой. Линейные напряжения сети равны 380 В.

Фазные напряжения при наличии уравнительного нулевого провода равны:

Сопротивления фаз нагрузки в соответствии с условием задачи:

Фазные токи определяются из соотношений:

Линейные токи в этой схеме равны фазным, а ток нулевого провода

I ˙ 0 = I ˙ A + I ˙ B + I ˙ C = 85 — j 127 + 82,6 — j 72,6 + 56,6 + j 92,3 = 224,2 — j 107,3 = 248 e j 25,6 °

Коэффициенты мощности определяются углами сдвига фаз токов и напряжений, т. е.

Задача #4521

В трехфазную сеть с действующим значением линейного напряжения 220 В и частотой 50 Гц включен потребитель, соединенный по схеме “треугольник” и имеющий равномерную нагрузку, состоящую из катушки м индуктивностью L = 0,3 Гн и последовательно включенного с ней резистора с активным сопротивлением 20 Ом в каждой фазе. Определить действующие значения линейных и фазовых токов, фазное напряжение, потребляемую полную, активную и реактивную мощности.

Полное сопротивление нагрузки в фазе:

Z = R 2 + X L 2 = R 2 + 2 π f L 2 = 20 2 + 2 × 3,14 × 50 × 0,3 2 = 96 О м

I л = 3 I ф = 3 × 2,3 = 3,98 ≈ 4 А

P = 3 U ф I ф cos ⁡ φ = 3 × 220 × 2,3 × 0,208 = 317 В т

Q = 3 U ф I ф sin ⁡ φ = 3 × 220 × 2,3 × 0,97 = 1470 в а р

S = 3 U ф I ф = 3 × 220 × 2,3 = 1520 В × А

Ответ: I_ф = 2,3 А; I_л = 4 А; U_ф = 220 В; P = 317 Вт; Q = 1470 вар; S = 1520 В × А.

Задача #4522

К трехфазной сети подключена несимметричная нагрузка, фазы которой характеризуются следующими параметрами: для фазы A R_A = 2,3 Ом и Х_CA = -1,5 Ом; для фазы В R_B = 1,8 Ом и X_LB = 3,1 Ом; для фазы C R_C = 1,3 Ом и Х_CC = -2,7 Ом. Определить фазные и линейные токи, коэффициенты мощности каждой фазы при соединении фаз нагрузки треугольником. Линейные напряжения сети равны 220 В.

Фазные и линейные напряжения при соединении нагрузки треугольником равны между собой:

U ф B = U л B = 220 e — j 120 ° В

U ф C = U л C = 220 e j 120 ° В

Сопротивления фаз нагрузки в соответствии с условием:

Фазные токи определяются из соотношений:

I ф A = U ф A Z A = 81,5 e j 33 ° А

I ф B = U ф A Z A = 61,1 e — j 180 ° А

I ф C = U ф C Z A = 73,3 e j 184 ° А

Линейные токи в данной схеме равны векторным разностям соответствующих фазных токов:

I ˙ л A = I ˙ ф A — I ˙ ф C = 149,5 e j 19 ° А

I ˙ л B = I ˙ ф B — I ˙ ф C = 137 e — j 161 ° А

I ˙ л C = I ˙ ф C — I ˙ ф B = 13 e — j 57 ° А

Коэффициенты мощности определяются углами сдвига фаз токов и напряжений, т. е.

Источник

примеры решений задач / 2.2 Трехфазные цепи / 1.3.2 Решение типовых задач1

Примеры решения типовых задач

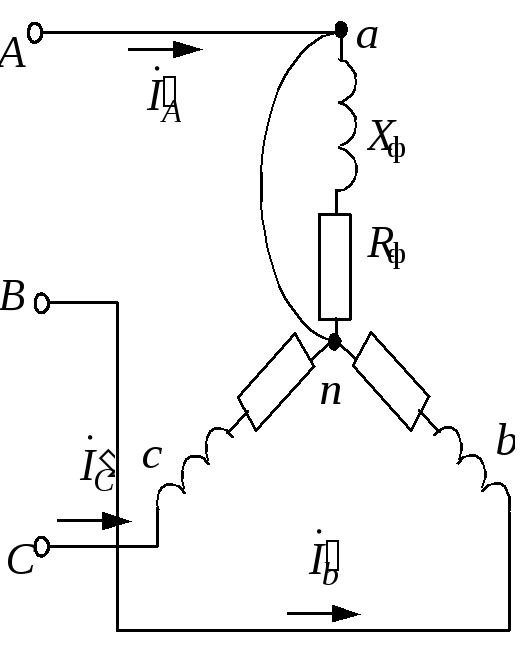
Задача 1.3.1 Трехфазный асинхронный двигатель включен в сеть 380 В по схеме «звезда». Параметры обмоток следующие: R_ф = 2 Ом, Х_ф = 8 Ом.

Требуется: изобразить схему включения двигателя в сеть; определить фазные и линейные токи; определить потребляемую активную мощность; построить векторную диаграмму токов и напряжений; рассмотреть два аварийных режима – обрыв и короткое замыкание фазы А.

Т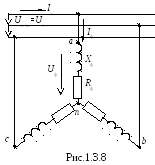рехфазный асинхронный двигатель является симметричной активно-индуктивной нагрузкой, поэтому включается в сеть по схеме «звезда» без нейтрального провода. Его схема замещения представлена на рис. 1.3.8

Номинальное напряжение сети является линейным напряжением, т. е. , тогда фазное напряжение

Поскольку нагрузка симметричная, то расчет можно проводить для одной фазы.

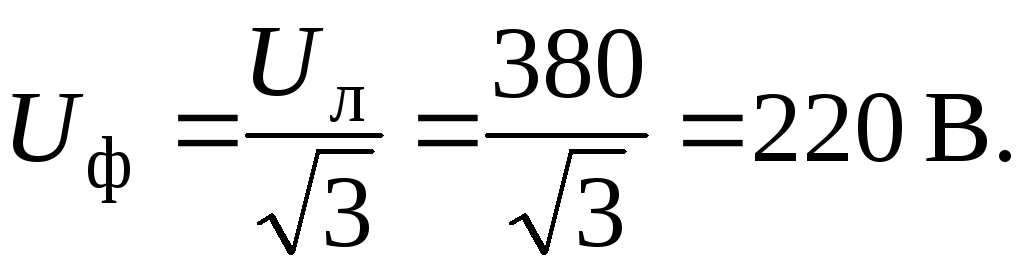
Полное сопротивление фазы

.

Для схемы «звезда» линейный ток 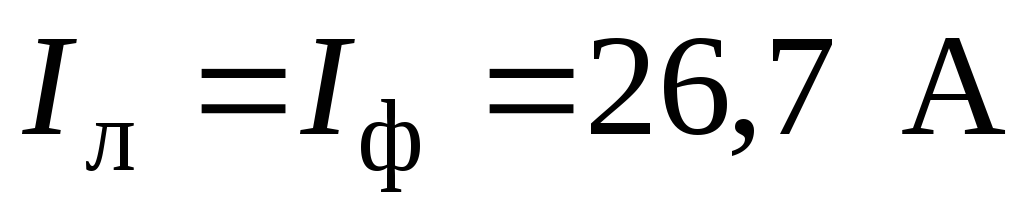. Потребляемая активная мощность

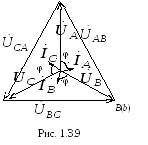
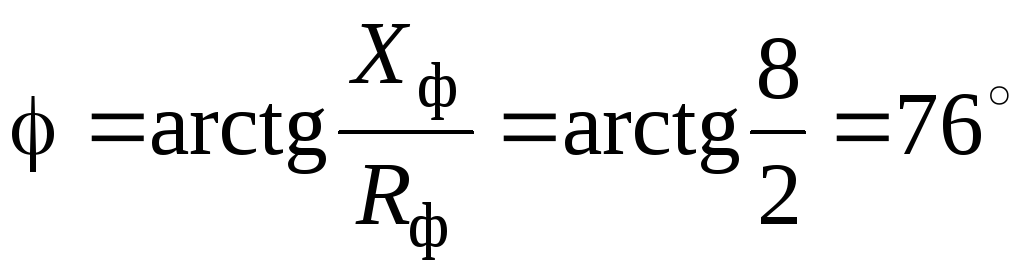
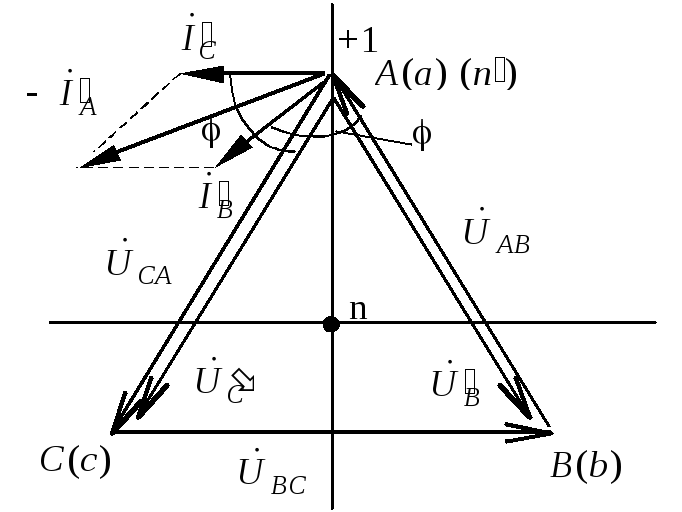
где  — фазовый угол,

.

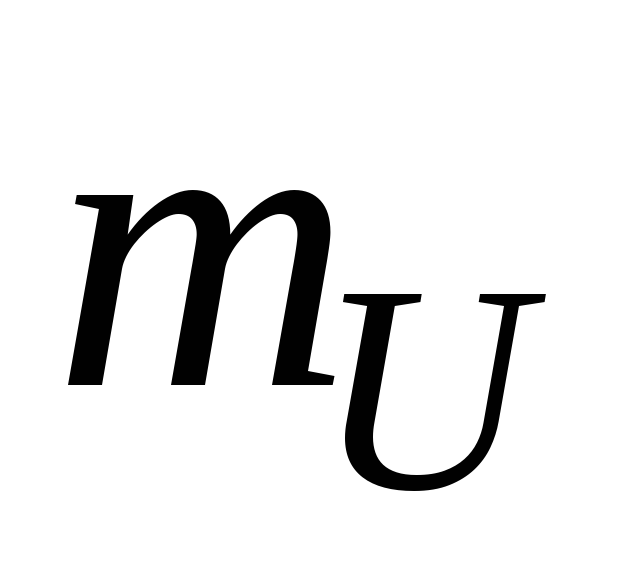
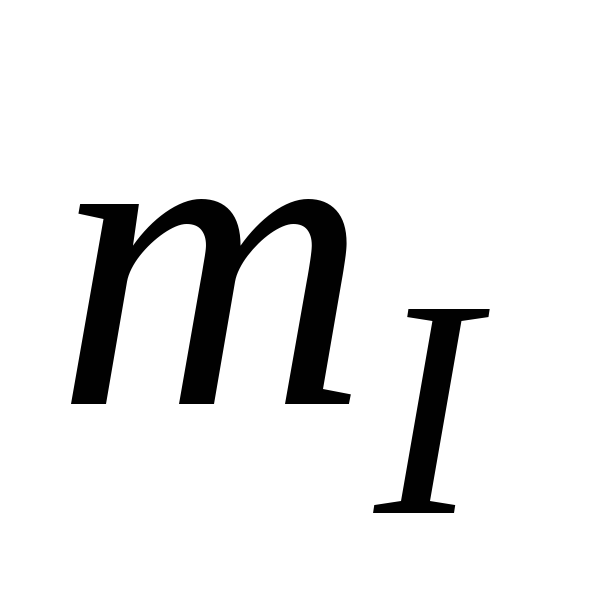
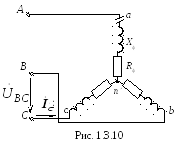
Векторная диаграмма токов и напряжений показана на рис. 1.3.9. Для построения векторной диаграммы необходимо выбрать масштабы напряжений и токов .

Рассмотрим аварийный режим работы– обрыв фазы А (рис.1.3.10).

В этом случае трехфазная цепь превращается в однофазную , причем фазы b и с оказываются включенными последовательно на линейное напряжение , т. е. на каждую из этих фаз падает напряжение

.

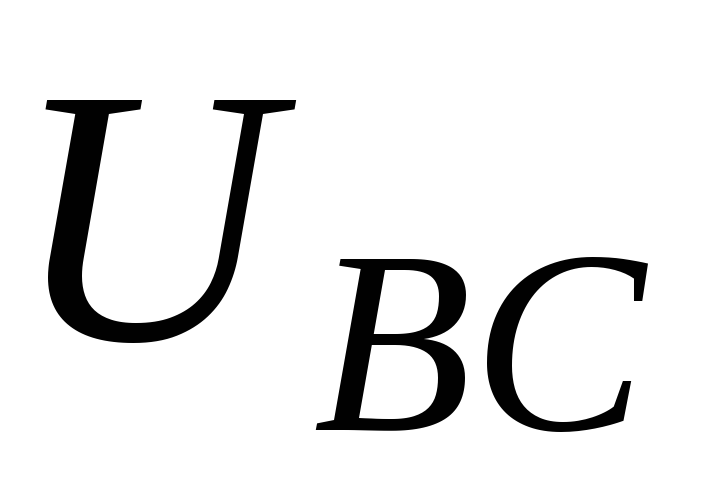
Как видно из расчета, потребляемая мощность снизилась почти в два раза.

Если обрыв фазы произошел внутри самого двигателя (обрыв обмотки), то эта обмотка оказывается под повышенным напряжением , что видно из векторной диаграммы (рис.1.3.11). Неповрежденные обмотки находятся под пониженным напряжением, что не опасно для них.

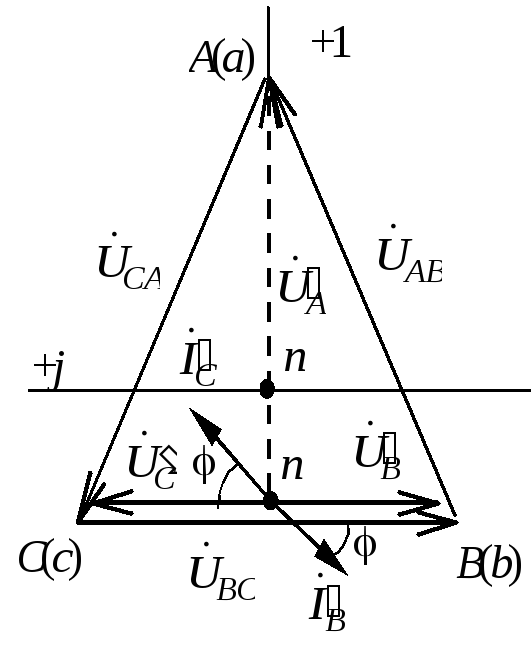
Рассмотрим аварийный режим работы – короткое замыкание фазы «а» (рис. 1.3.12, а, б).

При коротком замыкании фазы нейтральная точка оказывается связана с питающей точкой А, значит, неповрежденные фазы b и с окажутся включенными на линейное напряжение 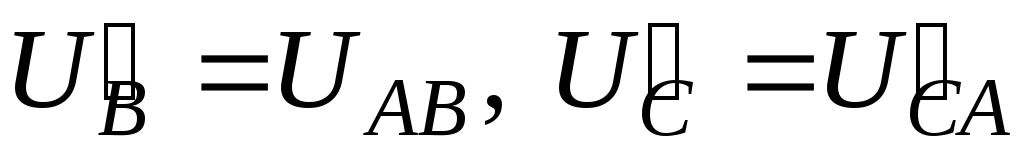, что видно из векторной диаграммы.

Токи в неповрежденных фазах

.

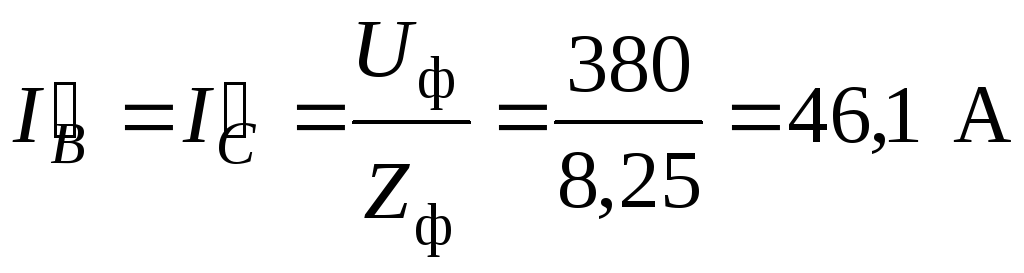
Ток в фазе а равен геометрической сумме токов и ( по векторной диаграмме составляет примерно 69 А).

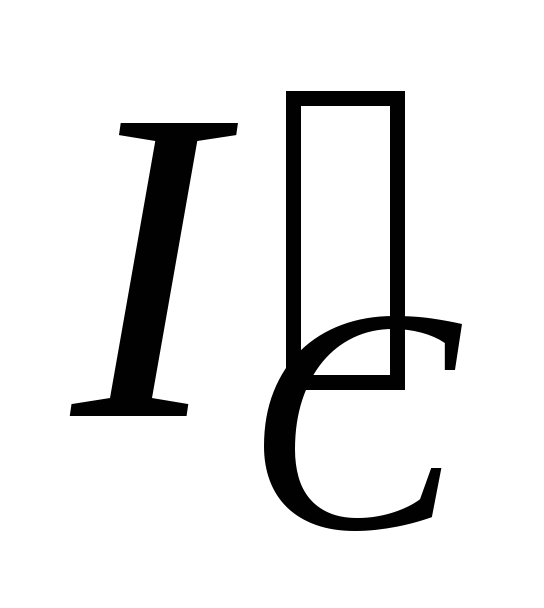
Задача 1.3.2. Три однофазных приемника включены в трехфазную сеть с напряжением 380 В по схеме “звезда с нейтральным проводом”. Сопротивления приемников: 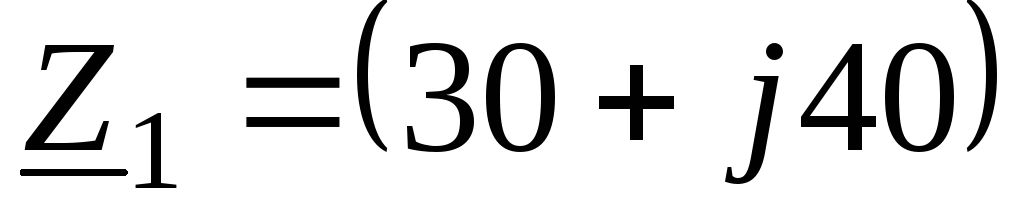Ом; Ом; Ом.

Требуется изобразить схему включения приемников; определить токи в проводах сети; построить векторную диаграмму токов и напряжений; вычислить активную, реактивную и полную (кажущуюся) мощности.

Схема включения приемников принципиальная и расчетная представлены на рис. 1.3.13, а,б.

Наличие нейтрального провода обеспечивает симметричную систему фазных напряжений на приемниках. Напряжение сети – линейное напряжение

В.

Система фазных напряжений в комплексной форме

Для схемы “звезда“ фазные и линейные токи равны между собой и составляют

Ток в нейтральном проводе

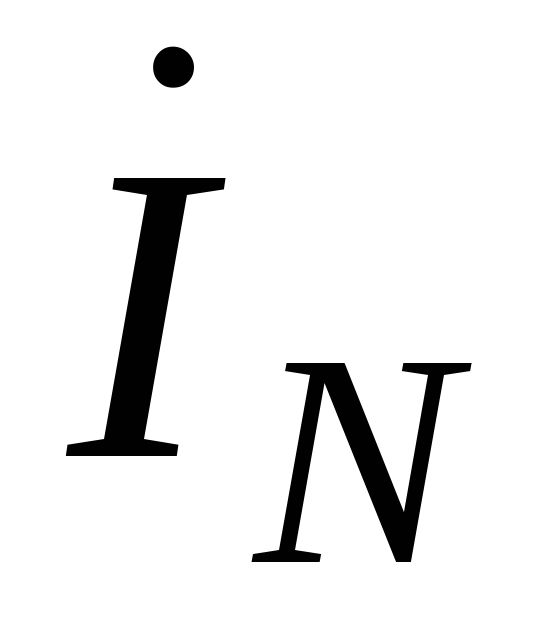
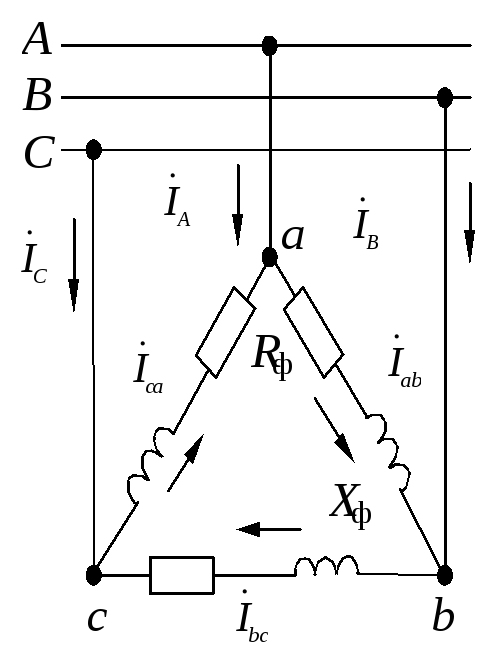
При построении векторных диаграмм фазные и линейные напряжения и токи строятся относительно комплексных осей откладываются с учетом начальных фаз. Ток в нейтральном проводе – это результат геометрического сложения векторов фазных токов, и его расположение и длина должны соответствовать расчетному значению (рис. 1.3.13).

Задача 1.3.3. К трехфазной системе напряжением 380 В подключены три одинаковых приемника (R_Ф = 3 Ом, X_LФ = 4 Ом), соединенные по схеме “треугольник“ (рис.1.3.14). Определить токи в фазных и линейных проводах и потребляемую мощность (активную, реактивную, полную). Построить векторную диаграмму токов и напряжений.

Рассмотреть аварийные режимы – обрывы фазного и линейных проводов.

Нагрузка фаз одинакова, поэтому расчет проводится для одной фазы.

Напряжение сети — это линейное напряжение, в схеме “треугольник “ U_ф = U_л = 380 В.

Комплексное сопротивление фазы:

где

линейные токи (только для симметричной нагрузки):

Активная мощность, потребляемая нагрузкой:

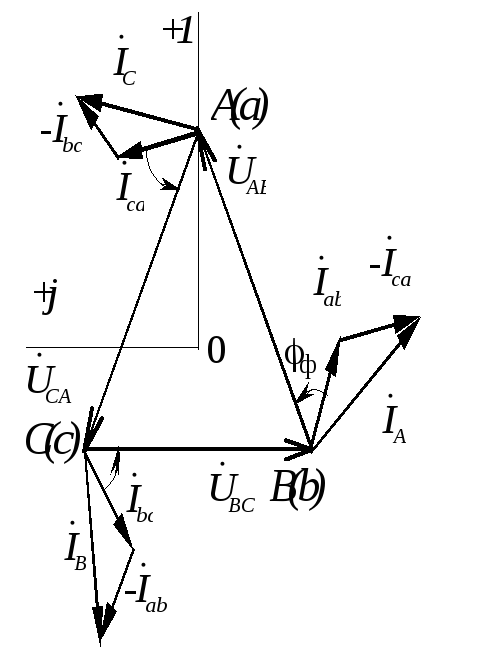
Векторная диаграмма может быть построена в двух вариантах в зависимости от изображения системы напряжений (рис.1.3.15 ). Предварительно выбирают масштабы тока и напряжения.

Фазные токи отстают от соответствующих напряжений на угол _Ф = 53. Линейные токи находятся из соотношений:

Рассмотрим обрыв фазы “аb” (рис.1.3.16,а). Определим токи в неповрежденных фазах и в линии, построим векторную диаграмму токов и напряжений.

Рис. 1.3.16

Токи в неповрежденных фазах не изменяются, так как не изменяются напряжения:

Линейные токи по первому закону Кирхгофа (с учетом ):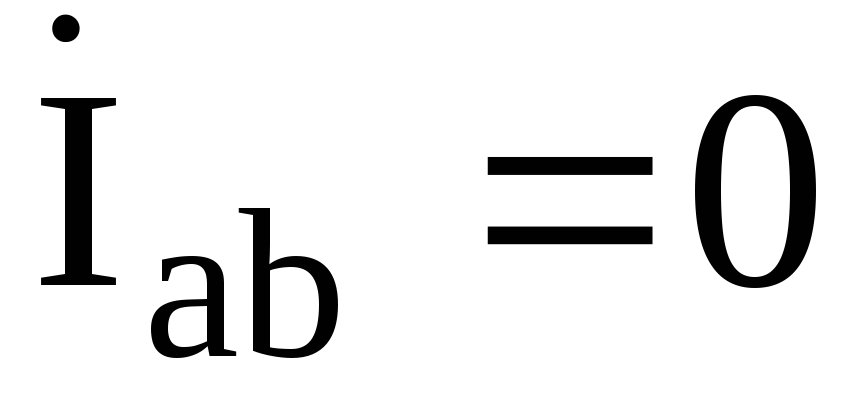

.

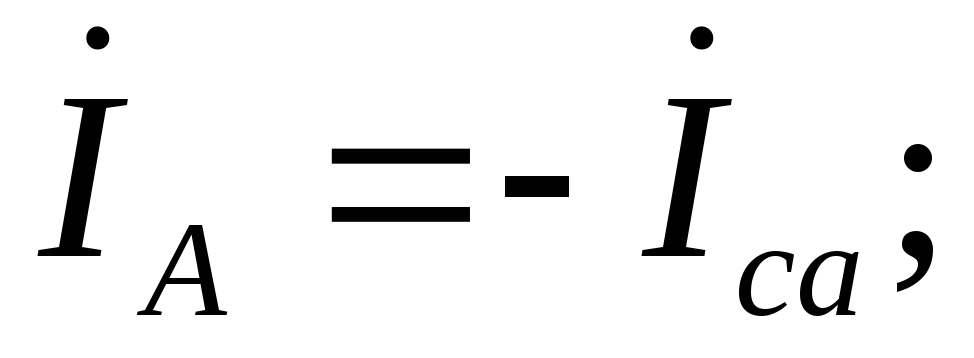
Из этих уравнений следует, что действующие значения линейных токов и равны действующим значениям фазных токов , а у линейного тока действующее значение не изменяется

Векторная диаграмма токов и напряжений строится аналогично симметричному режиму и приведена на рис.1.3.16,б.

Рассмотрим обрыв линейного провода А (рис.1.3.17,а). Определим фазные и линейные токи и построим векторную диаграмму токов и напряжений.

К приемнику подводится только напряжение

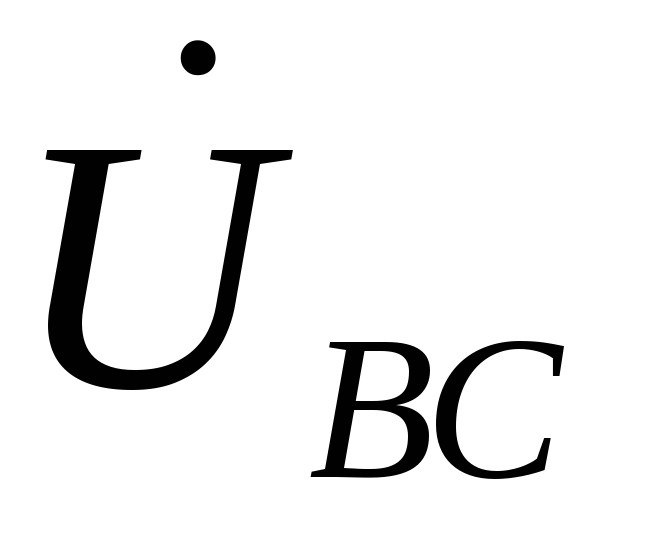
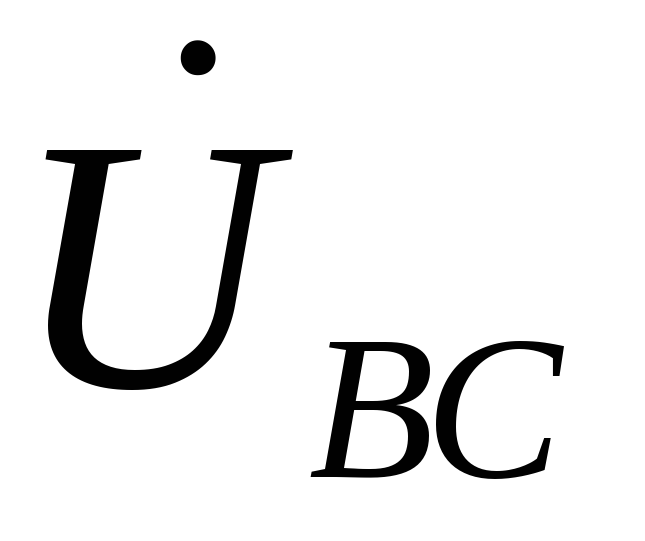
Сопротивление фазы “bс” включено на полное напряжение , а равные сопротивления фаз “аb” и ”са” включены последовательно друг с другом, причем к каждому из них подведена половина напряжения .

Сеть становится аналогичной однофазной с двумя параллельными ветвями:

Ток фазы “bс” не изменяется:

линейные токи ( при ) :

Векторная диаграмма токов и напряжений представлена на рис. 1.3.17,б.

Задача 1.3.4 В трехфазную сеть напряжением 380 В, частотой f = 50 Гц включен трехфазный асинхронный двигатель по схеме “треугольник“. Потребляемая активная мощность P = 1,44 кВт, коэффициент мощности cos = 0,85. Определить потребляемый двигателем ток, токи в обмотках двигателя, активное и индуктивное сопротивления, индуктивность катушек, полную и реактивную потребляемые мощности.

Двигатель является симметричной нагрузкой, поэтому расчет ведем на фазу.

Сеть маркируется линейным напряжением, поэтому U_Л = 380 В.

При соединении по схеме “треугольник“ U_Л = U_Ф= 380 В.

Активная мощность, потребляемая нагрузкой,

отсюда фазный ток, протекающий в обмотках двигателя:

Потребляемые двигателем токи — линейные токи:

Полное сопротивление фазы обмотки двигателя:

Ом,

Ом,

Ом.

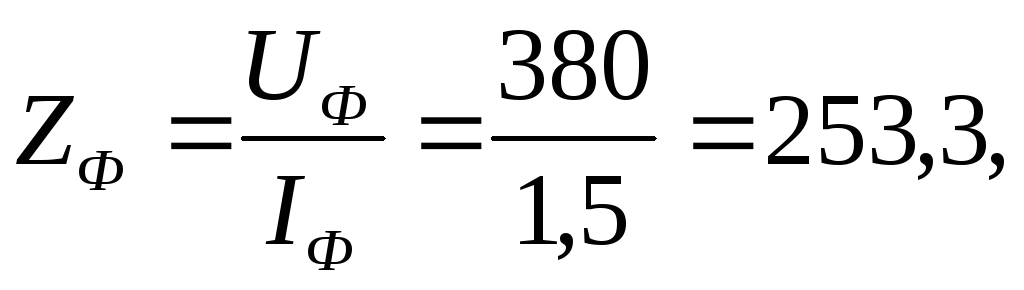
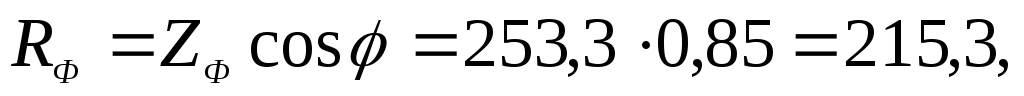
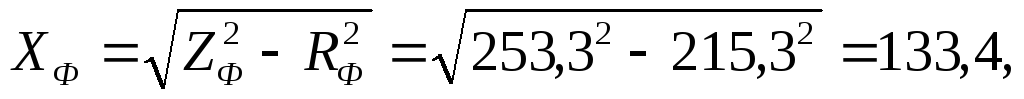
Индуктивность обмотки определяется из выражения

,

Гн.

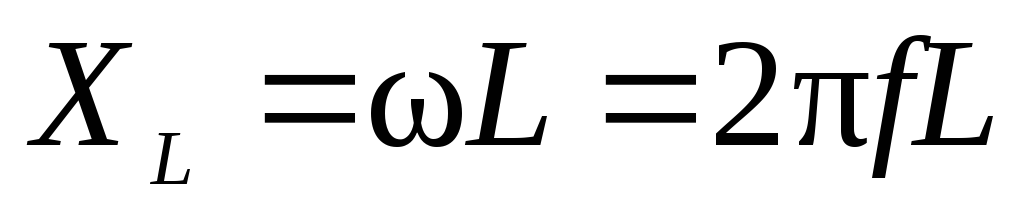
Полная потребляемая мощность:

кВА;

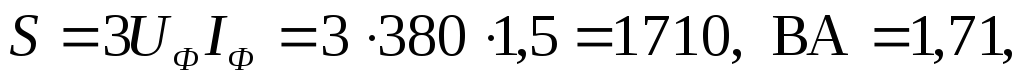
Задача 7.3 К трехпроводной трехфазной линии с напряжением 380 В подключены три однофазных приемника с параметрами: R₁= 5 Ом, R₂= 6 Ом, X_L2= 8 Ом, R₃=4 Ом, X_C3= 3 Ом. Определить токи в фазах и линейных проводах, активную, реактивную и полную мощности и построить векторную диаграмму токов и напряжений.

Однофазные приемники к трехпроводной сети подключаются по схеме “треугольник“ (рис.1.3.18).

Нагрузка несимметричная, ток каждой фазы нужно считать отдельно. Исходная система напряжений:

Комплексные сопротивления фаз:

Ом;

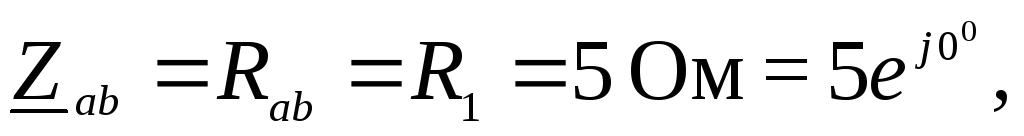
Рис. 1.3.18

Ом;

Ом;

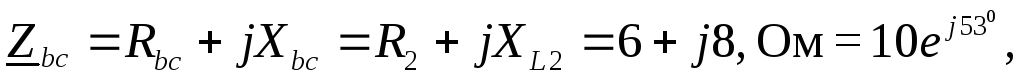
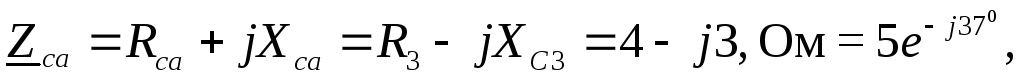
Сумма линейных токов должна равняться нулю, и действительно,

здесь знак “минус” показывает, что преобладает емкостная нагрузка.

Векторные диаграммы токов и напряжений в двух вариантах (для разного представления исходной системы напряжений) приведены на рис.1.3.19.

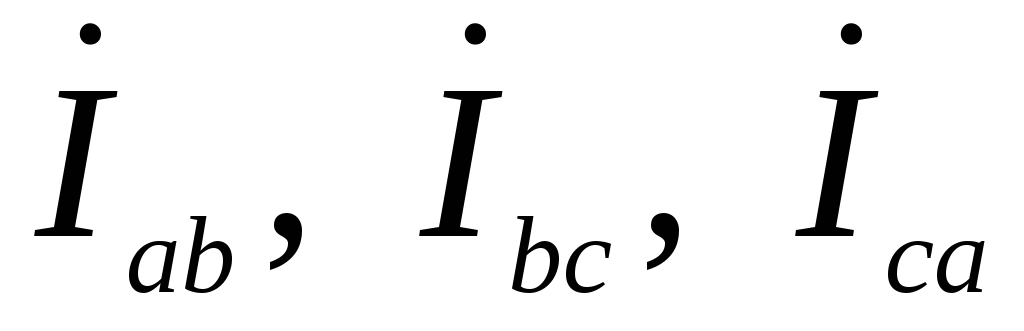
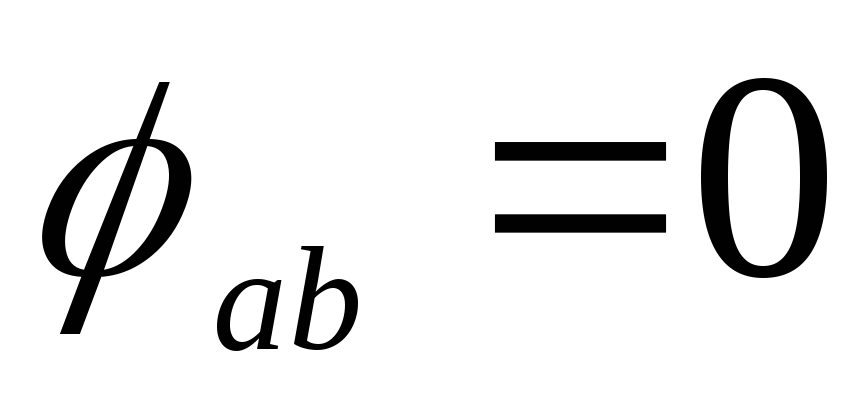
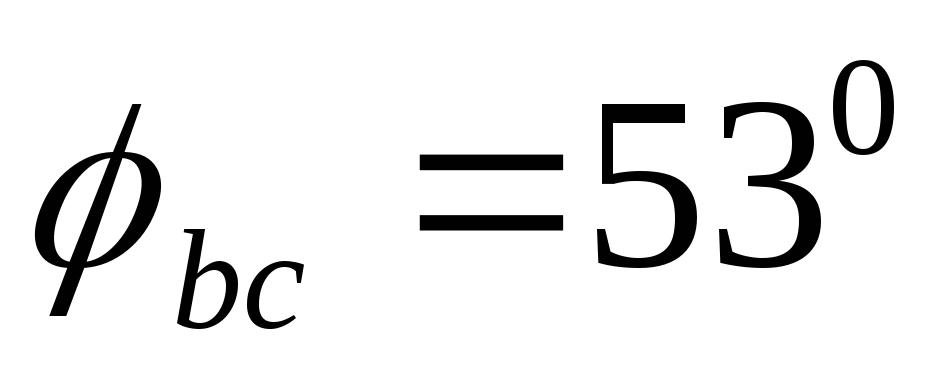
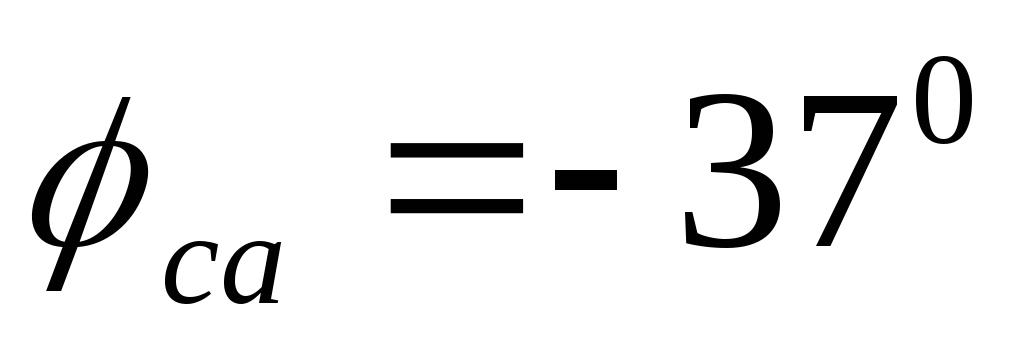
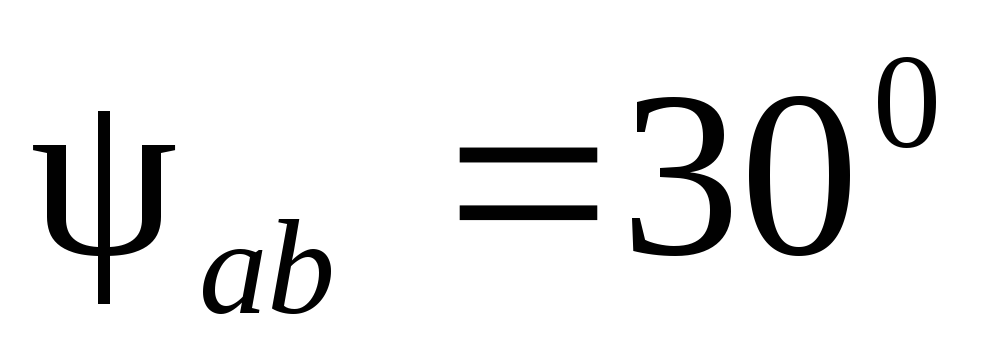
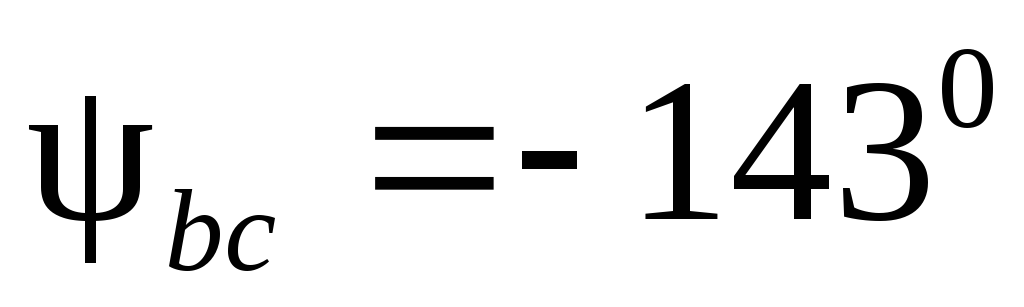
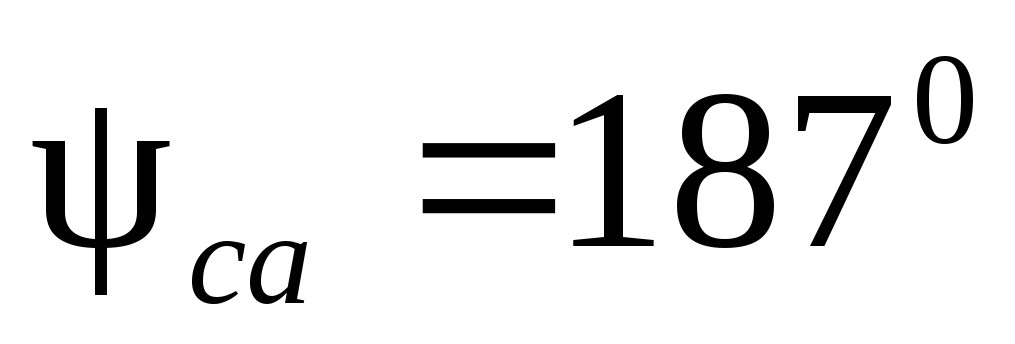
Предварительно выбирают масштабы тока и напряжения. Векторы фазных токов откладывают относительно векторов соответствующих напряжений под углами , , или в соответствии с полученными их начальными фазами ; ; . Затем по первому закону Кирхгофа строят векторы линейных токов , длина и направление которых должны соответствовать расчетным данным.

Рис.1.3.19 Векторные диаграммы токов и напряжений несимметричной нагрузки

Источник