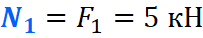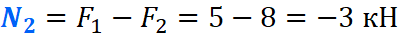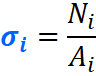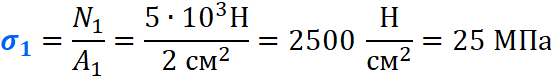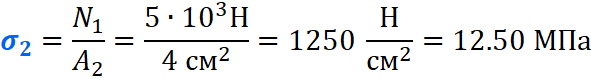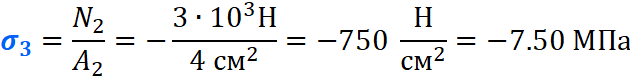Найти нормальное напряжение в конце участка сопромат

Как определить нормальное напряжение?

Автор: Константин Вавилов · Опубликовано 02.02.2016 · Обновлено 28.11.2017

Сегодня будем говорить о том, как определить нормальное напряжение при растяжении (сжатии). Долго говорить не придется, так как определяется оно элементарно.

Формула для нахождения нормального напряжения следующая:

То есть это отношение продольной силы (N) к площади поперечного сечения (A), на которой действует эта сила.

Пример определение нормальных напряжений

Посмотрим, как на практике пользоваться этой формулой. Например, возьмем брус с постоянным поперечным сечением, на который действует кучка внешних сил. Вас просят найти максимальное нормальное напряжение, возникающее в поперечных сечениях бруса.

Ваша тактика будет такой: Сначала нужно определить продольные силы и по-хорошему построить эпюру, чтобы видеть наиболее опасное сечение, то есть сечение, в котором внутренняя сила максимальная.

В нашем случае продольную силу берем равной трем килоньютонам и делим на площадь поперечного сечения:

Итого получили максимальное напряжение равное 15 мегапаскалям, что для стального бруса совсем пустяк.

Источник

Построение эпюр при растяжении и сжатии: продольных сил и нормальных напряжений для ступенчатого стержня (бруса)

Автор: Константин Вавилов · Опубликовано 23.11.2017 · Обновлено 14.03.2021

Приветствую, друзья! Сегодня дебютирует наш курс – «сопромат для чайников», Вы находитесь на сайте проекта SoproMats, который связан с сопроматом и не только. На этой страничке будет выложен первый урок из заявленного экспресс курса, который связан с таким простейшим видом деформации как растяжение (сжатие). В частности, будем учиться строить эпюры для бруса (стержня), который загружен растягивающей и сжимающей силой. Как правило, такое домашнее задание, одним из первых, дают всем студентам, которые начинают знакомиться с сопроматом. После изучения материалов данного урока вы научитесь строить следующие эпюры: продольных сил и нормальных напряжений. Не пугайтесь мудреных названий, на самом деле все эти эпюры строятся очень просто. Что же давайте приступим к изучению!

Построение эпюры продольных сил

Так как это курс для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику. Если вы хотите более детально изучить рассматриваемые здесь вопросы, то могу предложить Вам другие материалы нашего сайта. Например, что касается данного блока статьи, то у нас есть материалы про продольную силу, где представлено полное досье на данный внутренний силовой фактор: что эта за сила, зачем нужна и т.д. Но если Вам некогда залазить в эти дебри, и хотите по-быстрому освоить продольную силу, то оставайтесь здесь, сейчас покажу как строится первая эпюра!

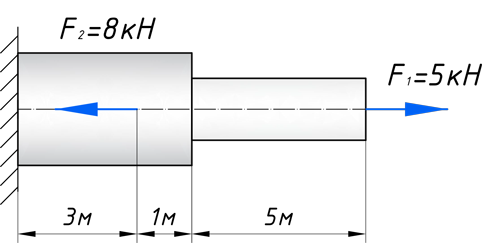
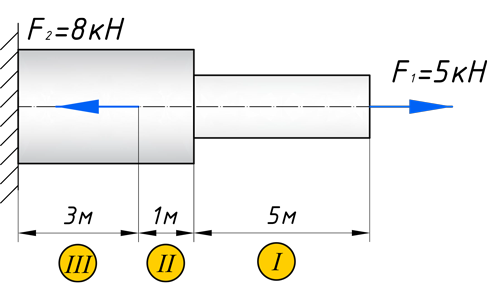
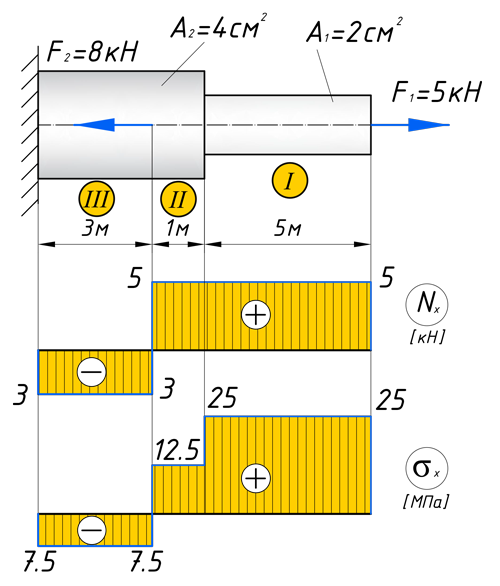
Кстати, вот объект нашего сегодняшнего исследования:

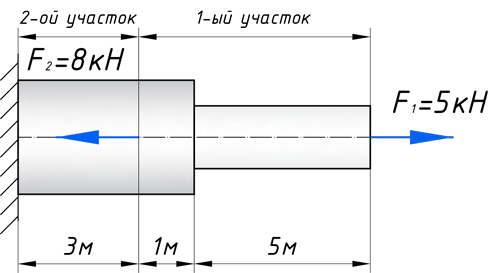
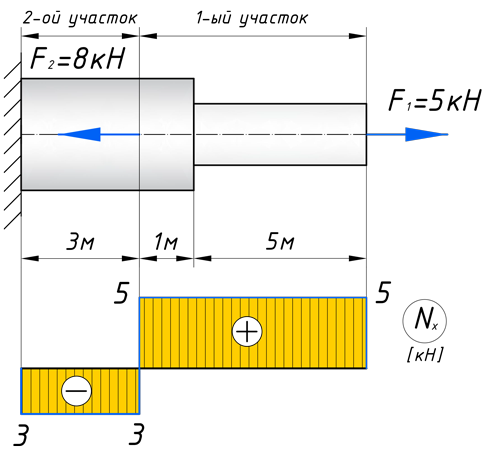
Чтобы построить эпюру продольных сил, нужно разбить наш брус на несколько участков, на которых эта эпюра будет иметь постоянное значение. Конкретно, для продольной эпюры, границами участков служат те точки, где прикладываются силы. То бишь, для нашего примера, нужно рассмотреть всего 2 участка:

Важно! На эпюру продольных сил, никак не влияет форма бруса, в отличие от других эпюр, которые будем дальше рассчитывать и строить.

На первом участке сила F₁ растягивает брус на величину 5кН, поэтому на этом участке, продольная сила будет положительной и равной:

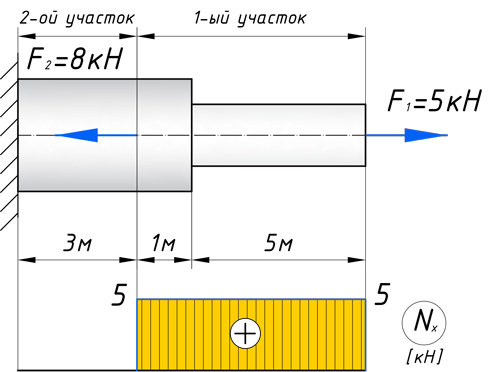
Откладываем это значение на графике. Эпюры в сопромате, принято штриховать перпендикулярно нулевой линии, а также для продольных сил, на эпюрах проставляются знаки:

На втором же участке, сила F₂ сжимает брус, тем самым в уравнение продольных сил, она пойдет с минусом:

Откладываем полученное значение на эпюре:

Вот так, достаточно просто, строится эта эпюра!

Построение эпюры нормальных напряжений

Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:

То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.

Для того чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:

Зададим брусу на первом участке (I) площадь поперечного сечения A₁=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A₂=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию. Также в задачах, часто, просят определить эти площади из условия прочности, с учетом допустимого напряжения, обязательно сделаю статью про это.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие). В рамках статьи, была рассмотрена достаточно простая расчетная схема, если Вы хотите развить свои навыки по построению эпюр, то приглашаю Вас на страничку про различные эпюры, где можно найти примеры расчета более сложных брусьев с распределенными нагрузками, где о каждой эпюре подготовлена отдельная статья.

Если Вам понравилась статья, расскажите о ней своим друзьям, подписывайтесь на наши социальные сети, где публикуется информация о новых статьях проекта. Также, там можно задать любой интересующий Вас вопрос о сопромате и не только.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Нормальные напряжения при изгибе

При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.

В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.

Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.

Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.

Допущения для вывода формул нормального напряжения: 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми. 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Рассмотрим балку произвольного сечения, но имеющую ось симметрии.Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде: (1), где y — плечо элементарной силы относительно оси х

Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения.

Выделим на среднем участке балки и рассмотрим участок длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе.

К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации

Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:, где -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:

Сократим на и приведем подобные члены, тогда получим:(2) Эта формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя.

Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии:, тогда с учетом формулы (2) имеем (3),т.е. нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим (3) в уравнение (1) и вынесем за знак интеграла дробь как постоянную величину, тогда имеем. Но выражение — это осевой момент инерции сечения относительно оси х — I_х. Его размерность см 4 , м 4

Тогда ,откуда (4) ,где — это кривизна изогнутой оси балки, а — жесткость сечения балки при изгибе.

Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: (5)

Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение (6) называют осевым моментом сопротивления сечения. Его размерность см 3 , м 3 . Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.

Тогда максимальные напряжения: (7)

Условие прочности при изгибе: (8)

При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.

Нейтральная линия. Вопрос о положении нейтральной линии.

При изгибе отсутствует продольная сила, поэтому можно записать Подставим сюда формулу нормальных напряжений (3) и получим Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х , и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения.

Условие (отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3) . По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны.

Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.

Характер эпюры σ для симметричных сечений относительно нейтральной линии, М Запись опубликована 18.04.2015 автором admin в рубрике Изгиб.

Источник