- Определить напряжение в точке а относительно общего провода 10v
- Кто сейчас на форуме
- Определить напряжение между точками
- Решение
- Правило напряжений Кирхгофа (второй закон Кирхгофа)
- Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?
- Демонстрация закона напряжений Кирхгофа в последовательной цепи
- Демонстрация закона напряжений Кирхгофа в параллельной цепи
- Справедливость закона Кирхгофа о напряжениях независимо от топологии цепи
- Использование закона Кирхгофа о напряжениях в сложной цепи
Определить напряжение в точке а относительно общего провода 10v
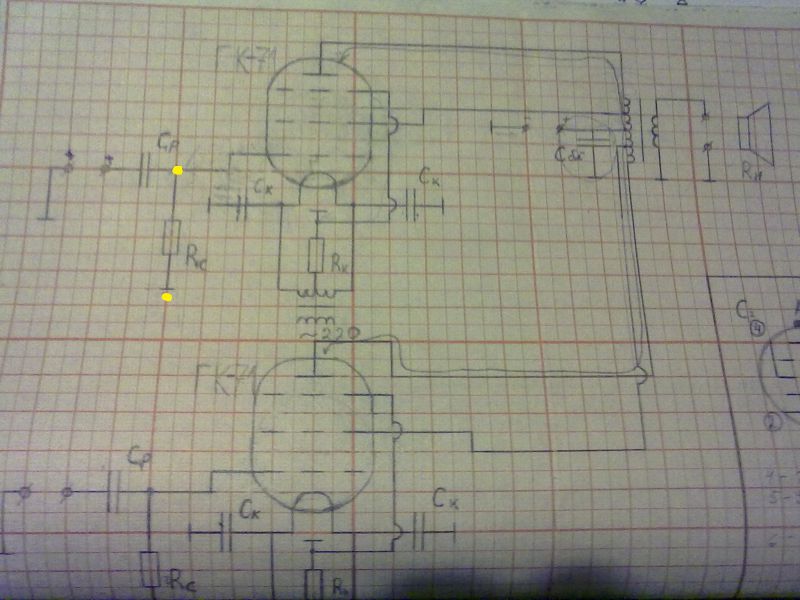
Собственно вопрос, на схеме определить потенциал точки ( указал желтой стрелкой)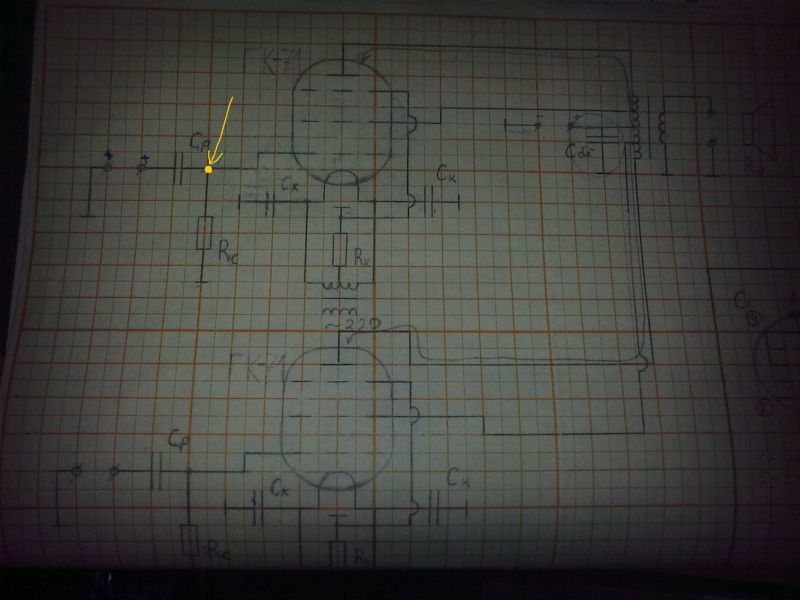
| Друг Кота |
| |
Карма: 39
Рейтинг сообщений: 563
Зарегистрирован: Вс янв 24, 2010 13:14:02
Сообщений: 4425
Откуда: Омск
Рейтинг сообщения: 0
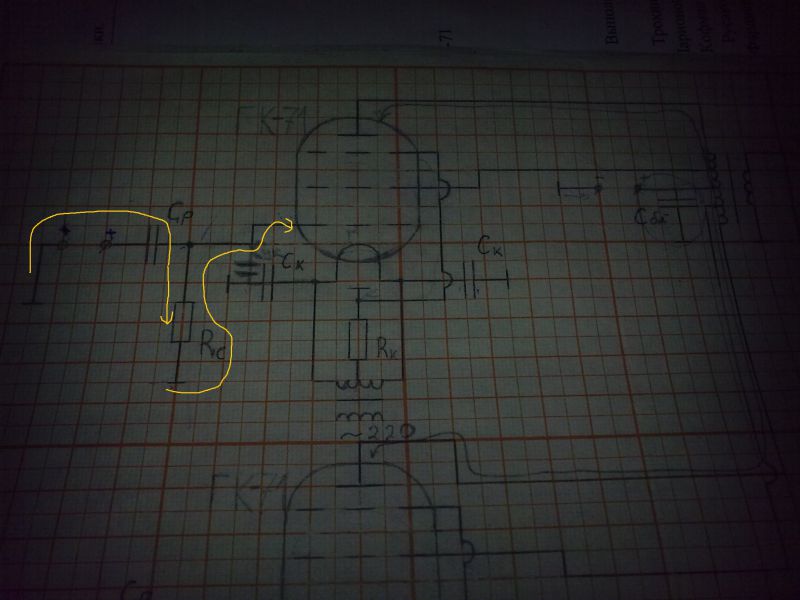
| JLCPCB, всего $2 за прототип печатной платы! Цвет — любой! Зарегистрируйтесь и получите два купона по 5$ каждый:https://jlcpcb.com/cwc Огромное спасибо за ответ. А могли бы подсказать еще, если не затруднить)) почему у нас будет потенциал 0 между сеткой и землей(указал желтыми точками) И что с входным током? Заранее спасибо. Сборка печатных плат от $30 + БЕСПЛАТНАЯ доставка по всему миру + трафарет |
| Друг Кота |
| |
Карма: 39
Рейтинг сообщений: 563
Зарегистрирован: Вс янв 24, 2010 13:14:02
Сообщений: 4425
Откуда: Омск
Рейтинг сообщения: 0
| Построение источников бесперебойного питания с двойным преобразованием, широко используемых в современных хранилищах данных, на базе карбид-кремниевых MOSFETs производства Wolfspeed позволяет уменьшить мощность потерь в них до 40%, а также значительно снизить занимаемый ими объем и стоимость комплектующих. |
| Поставщик валерьянки для Кота |
| |
Карма: 29
Рейтинг сообщений: 354
Зарегистрирован: Вс июл 11, 2010 14:39:04
Сообщений: 2458
Откуда: Россия.
Рейтинг сообщения: 0
| Компэл объявляет о значительном расширении складского ассортимента продукции Connfly. Универсальные коммутирующие компоненты, соединители и держатели Connfly сочетают соответствие стандарту ISO9001:2008, высокую доступность и простоту использования. На текущий момент на складе Компэл – более 300 востребованных на рынке товарных наименований с гибкой ценовой политикой. |
| Друг Кота |
| |
Карма: 39
Рейтинг сообщений: 563
Зарегистрирован: Вс янв 24, 2010 13:14:02
Сообщений: 4425
Откуда: Омск
Рейтинг сообщения: 0
| |
| Поставщик валерьянки для Кота |
| |
Карма: 29
Рейтинг сообщений: 354
Зарегистрирован: Вс июл 11, 2010 14:39:04
Сообщений: 2458
Откуда: Россия.
Рейтинг сообщения: 0
| Так вот как раз через этот резистор и попадает и смысл в нем есть и очень важный. А т.к. тока сетки у нас нет, то значит потенциал сетки относительно земли равен нулю, т.к. на сеточном резисторе ничего не падает. Смещение на сетке важно не относительно земли, а относительно катода. В данном случае можно или на сетку подать минус с отдельного источника или сделать катод более положительным, чем сетка, что и сделано в данном случае, что по сути одно и тоже, что сделать нулевой потенциал катода, а на сетку подать минус. В принципе полная аналогия с полевым транзистором у которого тоже нет тока затвора.
|
| Друг Кота |
| |
Карма: 39
Рейтинг сообщений: 563
Зарегистрирован: Вс янв 24, 2010 13:14:02
Сообщений: 4425
Откуда: Омск
Рейтинг сообщения: 0
| Я сам точно не знаю почему 0 ,но преподаватель сказал что 0 , и мне нужно объяснить почему 0 а я не знаю . А если взять вот эти две клеммы ( указал желтыми точками) то потенциал будет 0?(ну или что будет показывать вольтметр между этими точками?) И что в итоге с входным сигналом происходить? |
| Друг Кота |
| |
Карма: 39
Рейтинг сообщений: 563
Зарегистрирован: Вс янв 24, 2010 13:14:02
Сообщений: 4425
Откуда: Омск
Рейтинг сообщения: 0
| Так вот как раз через этот резистор и попадает и смысл в нем есть и очень важный. А т.к. тока сетки у нас нет, то значит потенциал сетки относительно земли равен нулю, т.к. на сеточном резисторе ничего не падает. Смещение на сетке важно не относительно земли, а относительно катода. В данном случае можно или на сетку подать минус с отдельного источника или сделать катод более положительным, чем сетка, что и сделано в данном случае, что по сути одно и тоже, что сделать нулевой потенциал катода, а на сетку подать минус. В принципе полная аналогия с полевым транзистором у которого тоже нет тока затвора. Кто сейчас на форумеСейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 10 Источник Определить напряжение между точкамиОпределить напряжение между точками Напряжение между точками AB Напряжение между узлами Напряжение между узлами схемы Решениепо моим расчетам I1=1.5, по вашему ответу тогда нужно чтобы «I3=1» как правильно расчитывается? Нет, только R3 и R4. А потом к ним в параллель R2. Добавлено через 2 минуты Сопротивление между точками подключения Напряженность между всеми точками однородного электрического поля одинакова? Найти напряжение между точками куба Источник Правило напряжений Кирхгофа (второй закон Кирхгофа)Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?Принцип, известный как правило напряжений Кирхгофа (открытое в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать следующим образом:
Под алгебраической я подразумеваю, помимо учета величин, учет и знаков (полярностей). Под контуром я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, наконец, обратно в исходную точку. Демонстрация закона напряжений Кирхгофа в последовательной цепиДавайте еще раз посмотрим на наш пример последовательной схемы, на этот раз нумеруя точки цепи для обозначения напряжений:
Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа: Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E2-1»), это означает напряжение в первой точке (2), измеренное по отношению ко второй точке (1). Напряжение, указанное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d». Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке позади, мы получили бы следующие показания:
Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого принципа: все измеренные напряжения в сумме равны нулю: В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3: Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, чтобы все компоненты были представлены на одной прямой линии:
Это всё та же последовательная схема, только с немного перераспределенными компонентами. Обратите внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах ориентированы в другую сторону (положительное слева и отрицательное справа). Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, противоположном источнику электродвижущей силы. Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:
Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с единственного R1 слева и продвигаясь по всей цепочке компонентов, мы увидели бы, как напряжения складываются алгебраически (до нуля):
Тот факт, что последовательные напряжения складываются, не должен быть тайной, но мы заметили, что полярность этих напряжений имеет большое значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую символ «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы видим, как измеряются бо́льшие значения напряжений (хотя и отрицательные), потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа). Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, за исключением того, что полярность напряжения батареи (минус слева, плюс справа) противоположна падениям напряжения на резисторах, поэтому при измерении напряжения на всей цепочке компонентов мы получаем 0 вольт. То, что мы должны получить ровно 0 вольт на всей линии, тоже не должно быть тайной. Глядя на схему, мы видим, что крайняя левая часть линии (левая сторона R1, точка номер 2) напрямую соединена с крайней правой частью линии (правая сторона батареи, точка номер 2), что необходимо для завершения схемы. Поскольку эти две точки соединены напрямую, они являются электрически общими друг с другом. Таким образом, напряжение между этими двумя электрически общими точками должно быть равно нулю. Демонстрация закона напряжений Кирхгофа в параллельной цепиПравило напряжений Кирхгофа (второй закон Кирхгофа) будет работать вообще для любой конфигурации схемы, а не только для простых последовательных цепей. Обратите внимание, как это работает для следующей параллельной схемы:
При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем: Обратите внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Поскольку мы начали наше пошаговое прохождение по контуру в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E2-2), которое, конечно, должно быть равно нулю. Справедливость закона Кирхгофа о напряжениях независимо от топологии цепиТот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего со справедливостью закона Кирхгофа о напряжениях. В этом отношении схема может быть «черным ящиком» (конфигурация ее компонентов полностью скрыта от нашего взгляда) с набором открытых клемм, между которыми мы можем измерить напряжение, – и правило напряжений Кирхгофа всё равно останется верным:
Попробуйте на приведенной выше диаграмме выполнить обход в любом порядке, начиная с любого вывода, и вернувшись к исходному выводу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю. Более того, «контур», который мы отслеживаем для второго закона Кирхгофа, даже не обязательно должен быть реальным путем протекания тока в прямом смысле этого слова. Всё, что нам нужно сделать, чтобы соответствовать правилу напряжений Кирхгофа, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между точками. Рассмотрим следующий абсурдный пример, проходя по «контуру» 2-3-6-3-2 в той же параллельной резисторной цепи:
Использование закона Кирхгофа о напряжениях в сложной цепиЗакон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):
Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:
Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру. Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4. Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие. Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:
Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:
Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта. Источник Adblockdetector |

 ?
?




 Определение напряжения между точками со множествами ЭДС
Определение напряжения между точками со множествами ЭДС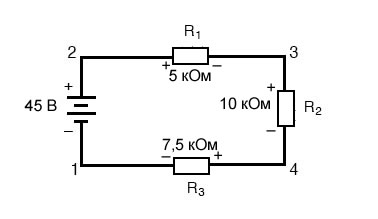 Рисунок 1 – Демонстрация закона напряжений Кирхгофа в последовательной цепи
Рисунок 1 – Демонстрация закона напряжений Кирхгофа в последовательной цепи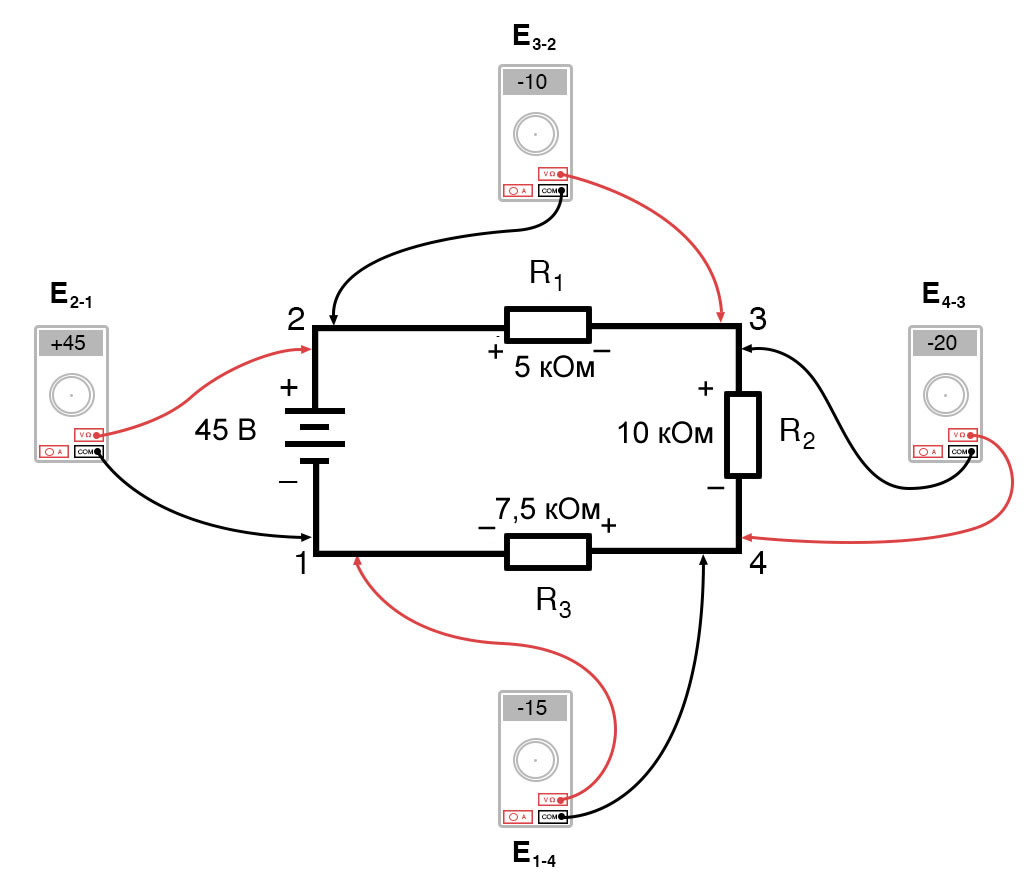 Рисунок 3 – Определение напряжений в последовательной цепи
Рисунок 3 – Определение напряжений в последовательной цепи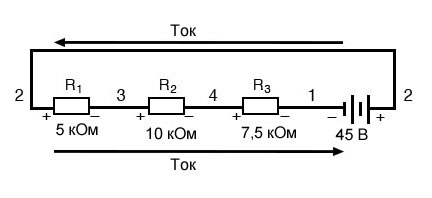 Рисунок 4 – Изменение представления последовательной цепи
Рисунок 4 – Изменение представления последовательной цепи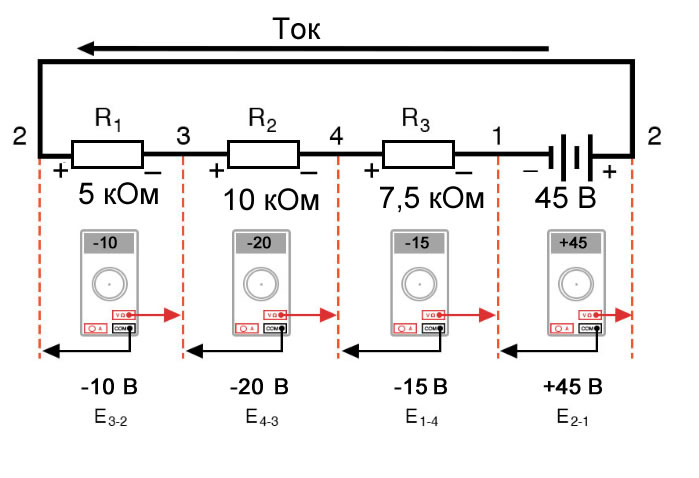 Рисунок 5 – Измерение напряжений в последовательной цепи
Рисунок 5 – Измерение напряжений в последовательной цепи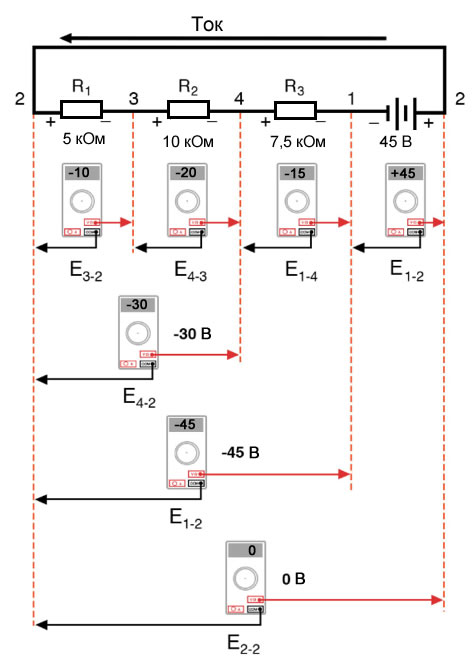 Рисунок 6 – Измерение суммы напряжений в последовательной цепи
Рисунок 6 – Измерение суммы напряжений в последовательной цепи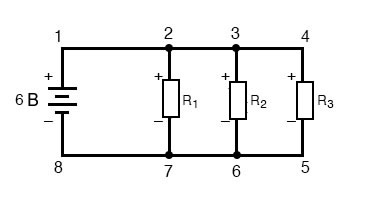 Рисунок 7 – Параллельная схема из резисторов
Рисунок 7 – Параллельная схема из резисторов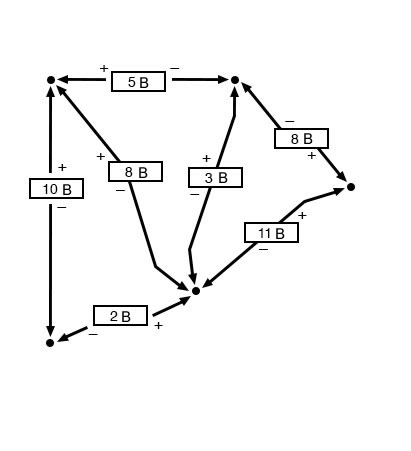 Рисунок 8 – Справедливость закона Кирхгофа напряжениях независимо от топологии схемы
Рисунок 8 – Справедливость закона Кирхгофа напряжениях независимо от топологии схемы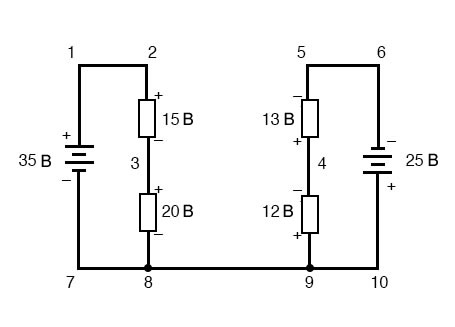 Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи
Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи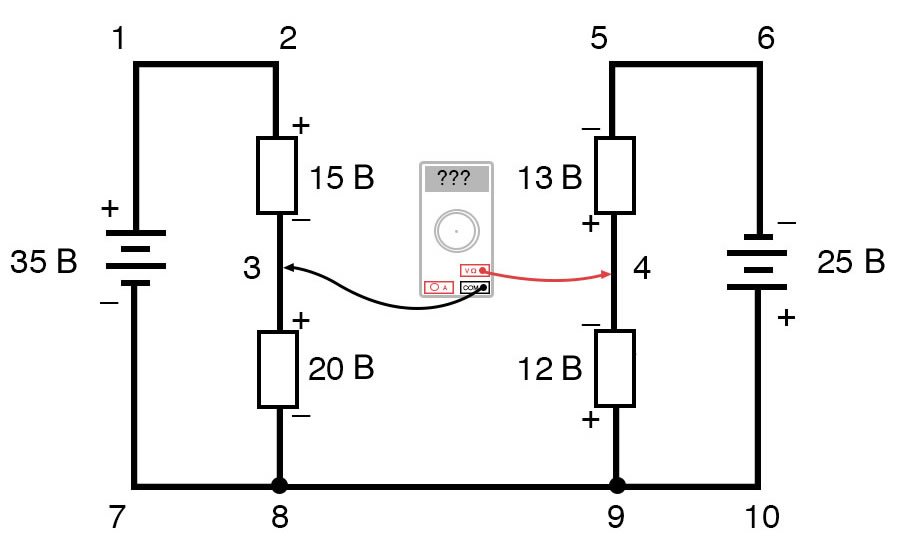 Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3 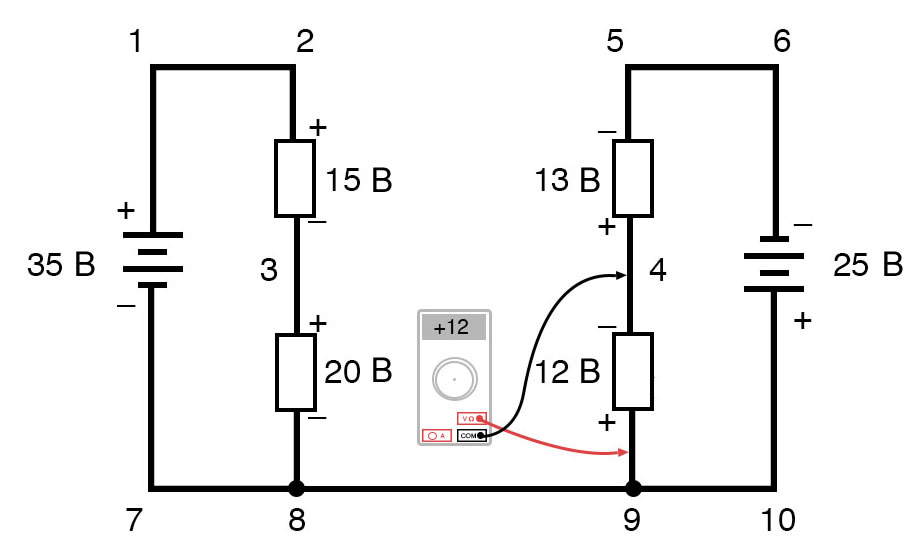 Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4
Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4 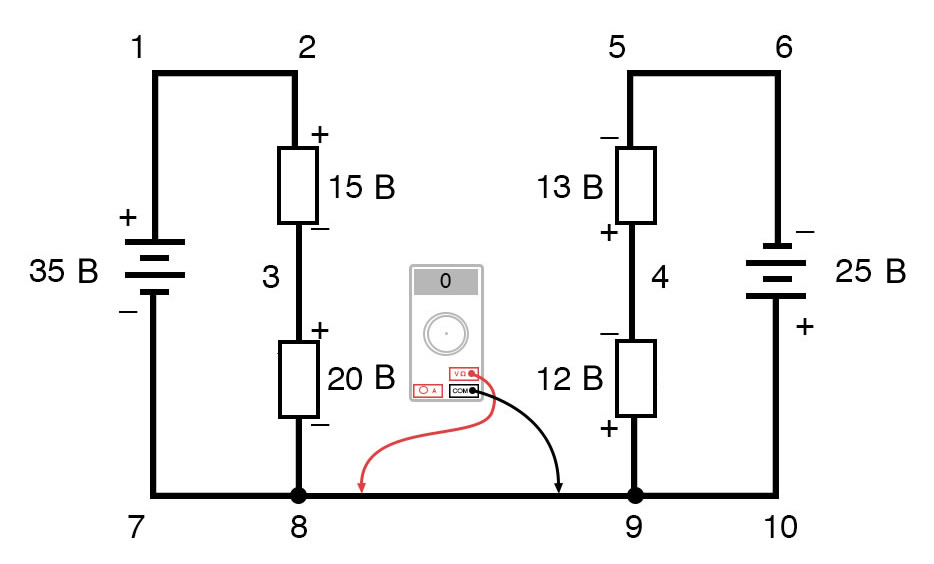 Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9
Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9 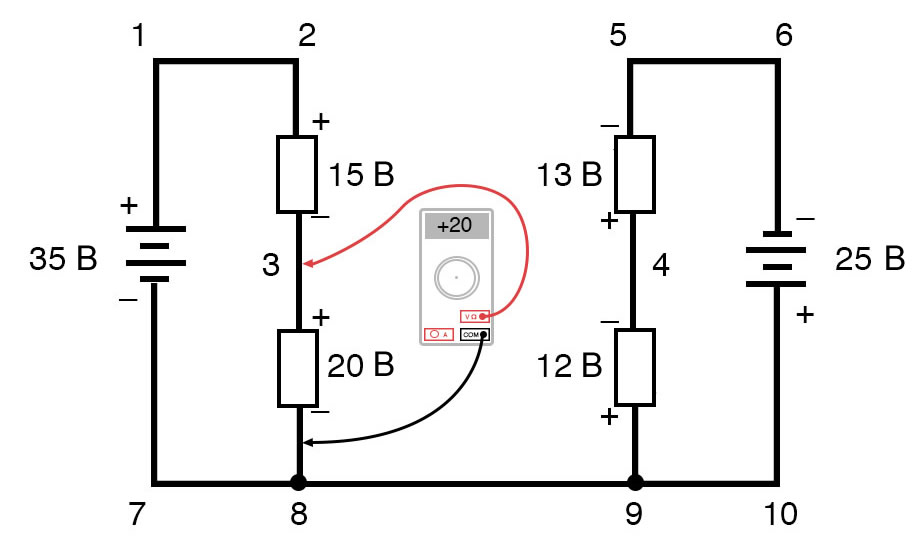 Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8
Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8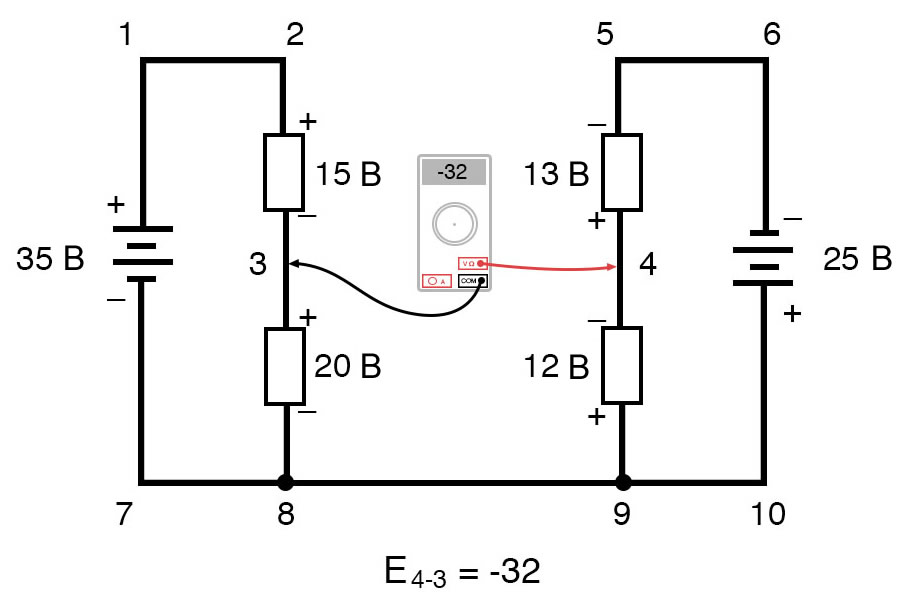 Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3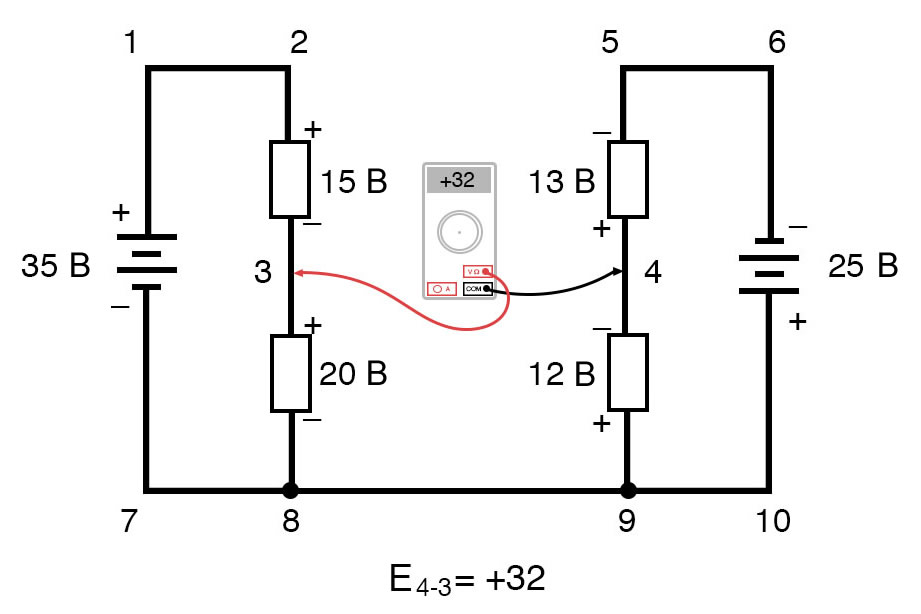 Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 4
Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 4