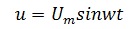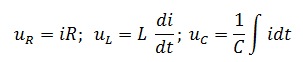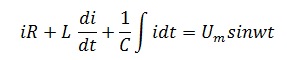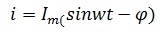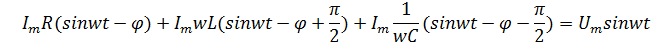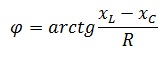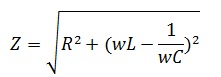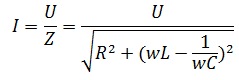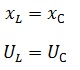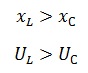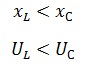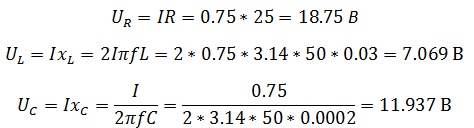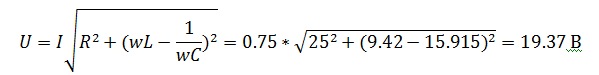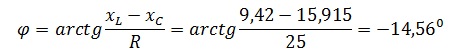Последовательная RLC-цепь
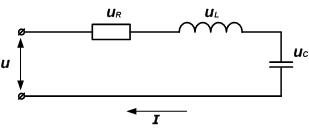
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
Напряжение на зажимах цепи
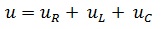
Выполнив подстановку, получим
Подставим в последнее выражение ток в цепи, зная, что он равен
В итоге получим выражение
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
Полное сопротивление RLС-цепи
Амплитудное значение тока
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
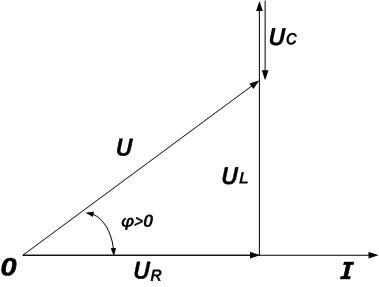
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
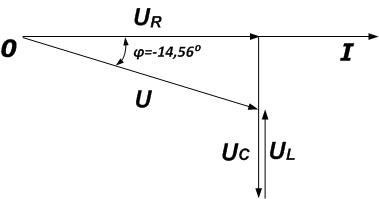
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
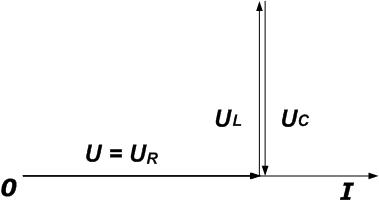
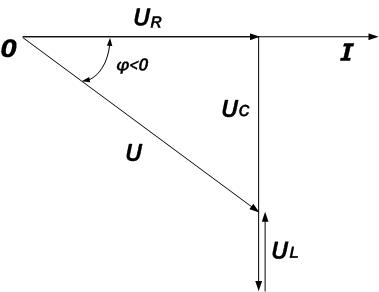
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
Источник
4.4. Переходные процессы в RLC-цепях
4.4. Переходные процессы в RLC-цепях
Рассмотрим переходные процессы в RLC-цепях на примере цепи последовательного колебательного контура рис. 4.3,а, потери в котором будем учитывать путем включения в цепь резистораR.
Рис.4.3. RLC-цепь (а) и переходные процессы в ней (б) и (в).
Переходные процессы в последовательном колебательном контуре при нулевых начальных условиях. Установим ключ К в положение 1, и подключим входное воздействие к контуру. Под действием подключенного источника u в контуре потечет ток i, который создаст напряжения uR, uL, uC .
На основании второго закона Кирхгофа для этого контура можно записать следующее уравнение

Учитывая, что 

Общее решение уравнения (4.34) будем искать в виде суммы свободной uС св и принужденной uС пр составляющих:

Свободная составляющая определяется решением однородного дифференциального уравнения, которое получается из (4.34) при u = 0

Решение (4.36) зависит от корней характеристического уравнения, которое получается из (4.36) и имеет вид

Корни этого уравнения определяются только параметрами цепи R, L ,C и равны

где α = R/2L – коэффициент затухания контура;

Из (4.38) видно, что корни р1 и р2 зависят от характеристического сопротивления контура 
при R > 2ρ вещественными и различными;
при R 2ρ свободная составляющая будет равна:

Пусть входное воздействие u = U = const, тогда принужденная составляющая uпр = U. Учитывая выражение (4.39) и что uпр = U выражение (4.35) примет вид:

Зная uС находим ток в контуре

Для определения постоянных интегрирования А1 и А2 запишем начальные условия для uC и i при t = 0:

Решая систему уравнений (4.42) получаем:


Подставляя А1 и А2 в уравнения (4.40) и (4.41) и учитывая, что в соответствии с (4.38) p1 p2=1/LC будем иметь:


Так как 

Графики изменения uС, i, uL в последовательном колебательном контуре при условии R > 2ρ приведены на рис. 4.3,б).
Моменты времени t1 и t2 определяются соответственно из условий



Анализ графиков, описываемых выражениями (4.43 – 4.45) показывает, что при R > 2ρ (при больших потерях) в контуре происходят апериодические процессы.
Рассмотрим процессы в контуре при R 2ρ, то корни р1 и р2 в (4.38) будут вещественны и различны и решение уравнения (4.36) будет иметь вид

Напряжение uC создает ток в цепи

Для определения постоянных интегрирования А1 и А2 положим t = 0 и учтем, что на момент коммутации uC = U, i = 0, тогда из (4.54) и (4.55) получим

Решая систему уравнений (4.56) находим


Подставляя А1 и А2 в (4.54) и (4.55) получаем уравнения для напряжения uC и тока i в цепи контура


Из выражений (4.57) и (4.58) видно, что при отключении входного воздействия от цепи контура, который имеет большое затухание (R > 2ρ) происходит апериодический разряд емкости С. Запасенная до отключения входного воздействия энергия в емкости WС = CU2/2 расходуется на покрытие тепловых потерь в резисторе R и создания магнитного поля в индуктивности L. Затем энергия электрического поля емкости WС и магнитная энергия индуктивности WL расходуется в резисторе R.
Найдем закон изменения напряжения uC и тока i в цепи, когда контур обладает малыми потерями, т.е. при условии R
Источник
Определить напряжение в цепи rlc





| ПРОСТЫЕ RLC-ЦЕПИ |
| ЭЛЕКТРОННЫЕ САМОДЕЛКИ СВОИМИ РУКАМИ | ||||||
| Автор: Administrator | ||||||
ПРОСТЫЕ RLC-ЦЕПИОСНОВНЫЕ ЛИНЕЙНЫЕ ПАССИВНЫЕ КОМПОНЕНТЫОсновные линейные компоненты электронных схем — это резистор, конденсатор и индуктивность. Если на клеммы этих компонентов подать напряжение и замерить ток, получим определенные законы их взаимодействия (табл. 2.2). Основной характеристикой резистора служит отношение напряжения к току: Табл. 2.2. Токи и напряжение пассивных компонентов называемое сопротивлением. Измеряется сопротивление в омах и является постоянной величиной. Производятся резисторы по различным технологиям и с широким диапазоном значений сопротивления — от нескольких ом до нескольких мегаом. Нужно отметить, что у реальных резисторов из-за рассеивания энергии (от 0,2 Вт до сотен ватт) формулы табл. 2.2 искажаются. Основное свойство катушки индуктивности — индуктивность. В проводнике возникает ток за счет наведенного напряжения, если проводник помещен в изменяющееся электромагнитное поле. Самоиндукция — случай, когда протекающий по проводнику ток возбуждает электромагнитное поле, которое наводит в нем самом напряжение самоиндукции. Взаимодействие двух проводников характеризуется взаимоиндукцией. Индуктивность измеряется в генри (Н) и вычисляется по формуле: Катушка индуктивности изготавливается в виде спирали из проводника. Количество витков спирали зависит от того, какую величину индуктивности необходимо получить. Сердечник катушки чаще всего изготавливают из материалов с магнитными свойствами, для того чтобы увеличить магнитный поток, а следовательно, и индуктивность. Нелинейные магнитные свойства сердечника могут привести к нелинейности вольт-амперной характеристики индуктивности. Электростатическое притяжение противоположных зарядов на двух проводниках, разделенных изолятором (или диэлектриком), вызывает такое свойство, как емкость. Она определяется как отношение заряда, накопленного в проводниках, разделенных изолятором, к напряжению, вызванному им: Накопленный заряд и в результате энергия связаны с электрическим полем в диэлектрике. Емкость измеряется в фарадах (Ф). Так как ток по своей сути это поток заряженных частиц между двумя противоположными зарядами, или, другими словами, скорость разряда конденсатора, то: Следовательно, уравнение (2.25) можно записать как: Иногда при использовании конденсаторов полезно помнить, что это накопитель или источник заряда. Изготавливаются конденсаторы из двух проводников с изолятором между ними. Номиналы конденсаторов бывают от нескольких пикофарад (10 12 Ф) до нескольких милифарад (10 3 Ф). Для каждого конденсатора установлены пределы напряжений, в которых он работает корректно. Если в качестве изолятора в конденсаторах применяется диэлектрик, то при определенной полярности зарядов на проводниках он работает как изолятор. При противоположной полярности — как проводник, поэтому при подключении таких конденсаторов необходимо соблюдать маркированную полярность. Чаще всего в электронных схемах конденсаторы используются как фильтры. В микросхемах также применяются конденсаторы. Источник Adblockdetector |