Баланс реактивной мощности и его связь с напряжением

Баланс реактивной мощности и его связь с напряжением

При выработке и потребители энергии на переменном токе равенству вырабатываемой и потребляемой электроэнергии в каждый момент времени отвечает равенство вырабатываемой и потребляемой не только активной, но и реактивной мощности.

Эти условия можно записать так:

∑Pг = ∑Pп = ∑Pн = ∑ΔP,

∑Qг = ∑Qп = ∑Qн = ∑ΔQ

где ∑Pг и ∑Qг — генерируемые активная и реактивная мощности станций за вычетом собственных нужд; ∑Pн, ∑Qн — активная и реактивная мощности потребителей; ∑ΔP, ∑ΔQ — суммарные потери активной и реактивной мощностей в сетях; ∑Pп, ∑Qп — суммарное потребление активной и реактивной мощностей.

Вышеприведенные уравнения являются уравнениями балансов активной и реактивной мощностей. Баланс реактивной мощности по всей системе в целом определяет некоторый уровень напряжения. Напряжения в узловых точках сети электрической системы в той или иной степени отличаются от среднего уровня, причем это отличие определяется конфигурацией сети, нагрузкой и другими факторами, от которых зависит падение напряжения. Баланс реактивной мощности для всей системы в целом не может исчерпывающе определить требования, предъявляемые к мощности источников реактивной мощности. Надо оценивать возможность получения необходимой реактивной мощности как по системе, так и по отдельным ее районам.

Необходимость в оценке баланса реактивной мощности возникает прежде всего при проектировании подсистемы регулирования напряжения — реактивной мощности АСУДУ (автоматизированной системы диспетчерского управления).

В ряде случаев оценка изменений условий баланса производится и в практике эксплуатации, например при вводе новых регулирующих устройств, установленных мощностей электростанций, изменениях схемы сети.

Нарушение баланса реактивной мощности приводит к изменению уровня напряжения в сети. Если генерируемая реактивная мощность становится больше потребляемой (∑Qг > ∑Qп), то напряжение в сети повышается. При дефиците реактивной мощности (∑Qг

В дефицитных по активной мощности энергосистемах уровень напряжения, как правило, ниже номинального. Недостающая для выполнения баланса активная мощность передается в такие системы из соседних энергосистем, в которых имеется избыток генерируемой мощности.

Обычно энергосистемы дефицитные по активной мощности, дефицитны и по реактивной мощности. Однако недостающую реактивную мощность эффективнее не передавать из соседних энергосистем, а генерировать в компенсирующих устройствах, установленных в данной энергосистеме.

Источник

Потери и падение напряжения — в чем различия

_{В обычной жизни человека слова «потери» и «падение» применяются для обозначения факта снижения определенных достижений, но обозначают разную величину.}

_{При этом «потерями» обозначает утрату части, ущерб, уменьшение количества достигнутого ранее уровня. Потери нежелательны, но с ними можно мириться.}

_{Под словом «падение» понимается более серьёзный урон, связанный с полным лишением прав. Таким образом, даже иногда происходящие потери (скажем, кошелька) со временем могут привести к падению (например, уровня материальной жизни).}

_{В этом плане рассмотрим этот вопрос по отношению к напряжению электрической сети.}

_{Как образуется потери и падение напряжения}

_{Электроэнергия на большие расстояния передается по воздушным линиям от одной подстанции к другой.}

_{Провода ВЛ рассчитаны на передачу допустимой мощности и изготавливаются из металлических жил определенного материала и сечения. Они создают активную нагрузку с величиной сопротивления R и реактивную — X.}

_{На приемной стороне стоит трансформатор, преобразующий электроэнергию. Его обмотки обладают активным и ярко выраженным индуктивным сопротивлением XL. Вторичная сторона трансформатора понижает напряжение и передает его дальше потребителям, нагрузка которых выражается величиной Z и носит активный, емкостной и индуктивный характер. Она тоже оказывает влияние на электрические параметры сети.}

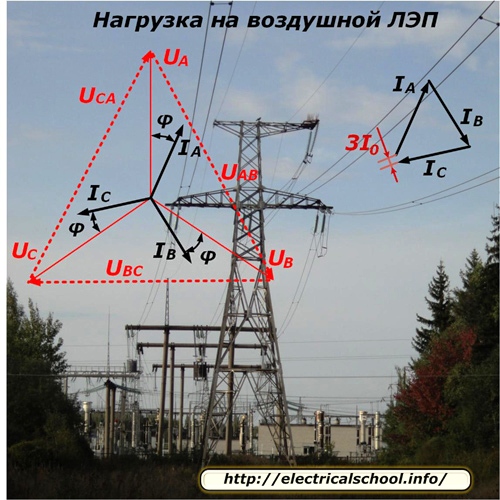
_{Напряжение, приложенное на провода ближайшей к передающей электроэнергию подстанции опоре ВЛ, преодолевает реактивное и активное сопротивление цепи в каждой фазе и создает в ней ток, вектор которого отклоняется от вектора приложенного напряжения на угол φ.}

_{Характер распределения напряжений и протекания токов по линии для симметричного режима нагрузки показан на картинке.}

_{Поскольку каждая фаза линии питает разное количество потребителей, которые к тому же случайным порядком отключаются или подключаются в работу, то идеально сбалансировать фазную нагрузку технически очень сложно. В ней всегда есть небаланс, который определяется векторным сложением токов фаз и записывается величиной 3I0. В большинстве расчетов им просто пренебрегают.}

_{Энергия, затраченная передающей подстанцией, частично расходуется на преодоление сопротивления линии и доходит до приемной стороны с небольшими изменениями. Эта доля характеризуется потерей и падением напряжения, вектор которого немного уменьшается по амплитуде и сдвигается по углу в каждой фазе.}

_{Как рассчитываются потери и падение напряжения}

_{Для понимания процессов, происходящих при передаче электроэнергии, удобна векторная форма представления основных характеристик. Различные математические методы расчета также базируются на этом способе.}

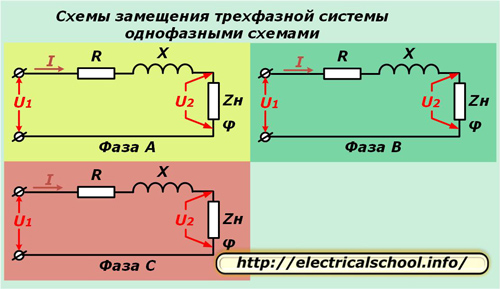
_{Чтобы упростить вычисления в трехфазной системе ее представляют тремя однофазными схемами замещения. Этот способ хорошо работает при симметричной нагрузке и позволяет анализировать процессы при ее нарушениях.}

_{В приведенных схемах активное R и реактивное X сопротивление каждого провода линии подключаются последовательно к комплексному сопротивлению нагрузки Zн, характеризуемой углом φ.}

_{Далее проводится расчет потери и падения напряжения в одной фазе. Для этого надо задать данные. С этой целью выбирается подстанция, принимающая энергию, на которой уже должна быть определена допустимая нагрузка.}

_{Величина напряжения каждой высоковольтной системы уже задана справочниками, а сопротивления проводов определяются по их длине, поперечному сечению, материалу и конфигурации сети. Максимальный ток в цепи задан и ограничен свойствами проводников.}

_{Поэтому для начала вычислений мы имеем: U2, R, X, Z, I, φ.}

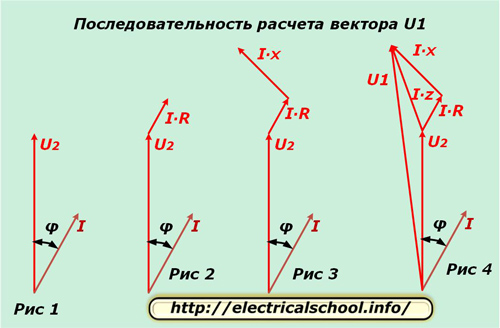
_{Берем одну фазу, например, «А» и откладываем для нее на комплексной плоскости вектора U2 и I, сдвинутые на угол φ, как показано на рисунке 1. Разность потенциалов на активном сопротивлении провода совпадает по направлению с током, а по величине определяется выражением I∙R. Этот вектор откладываем от окончания U2 (Рис. 2).}

_{Разность потенциалов на реактивном сопротивлении провода отличается от направления тока на угол φ1 и вычисляется произведением I∙X. Откладываем его от вектора I∙R (Рис. 3).}

_{Напоминания: за положительное направления вращения векторов на комплексной плоскости принято движение, противоположное ходу часовой стрелки. Ток, проходящий через индуктивную нагрузку, отстает по углу от приложенного напряжения.}

_{На рисунке 4 показано вычерчивание векторов разности потенциалов на общем сопротивлении провода I∙Z и напряжения на входе в схему U1.}

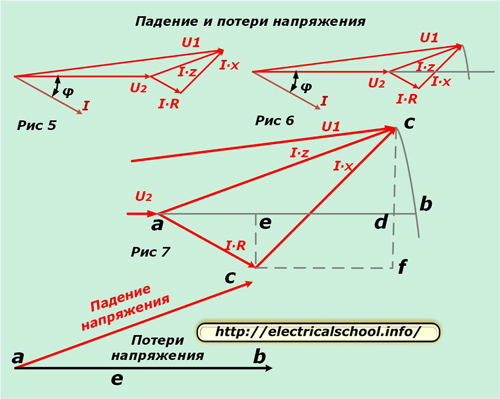
_{Теперь можно сравнивать вектора на входе в схему замещения и на нагрузке. Для этого расположим полученную диаграмму горизонтально (Рис. 5) и из начала координат проведем дугу с радиусом модуля U1 до пересечения с направлением вектора U2 (Рис. 6).}

_{На рисунке 7 показано увеличение треугольника для наглядности и проведение вспомогательных линий, обозначение характерных точек пересечения буквами.}

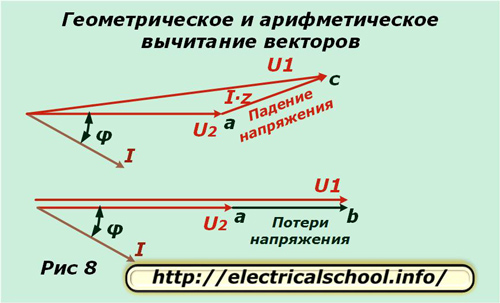
_{Внизу картинки показано, что получившийся вектор ac называют падением напряжения, а ab — потерями. Они отличаются по величине и направлению. Если вернуться к исходному масштабу, то будет видно, что ас получен в результате геометрического вычитания векторов (U2 из U1), а ab — арифметического. Этот процесс показан на картинке ниже (Рис. 8).}

_{Вывод формул для расчета потери напряжения}

_{Теперь вернемся к рисунку 7 и обратим внимание, что отрезок bd очень маленький. По этой причине при расчетах им пренебрегают, а потери напряжения рассчитывают по длине отрезка ad. Он состоит из двух отрезков ae и ed.}

_{Поскольку ae=I∙R∙cosφ, а ed=I∙x∙sinφ, то потери напряжения для одной фазы можно вычислить по формуле:}

_{Считая нагрузку симметричной во всех фазах (условно пренебрегая 3I0) можно математическими методами вычислить потери напряжения в линии .}

_{Если правую часть этой формулы умножить и разделить на напряжение сети Uн, то получим формулу, позволяющую выполнять р асчет потерь напряжения через мощности .}

_{Величины активной P и реактивной Q мощностей можно снимать с показаний электросчетчиков линии.}

_{Таким образом, потери напряжения в электрической схеме зависят от:}

_{активного и реактивного сопротивления цепи;}

_{составляющих приложенной мощности;}

_{величины приложенного напряжения.}

_{Вывод формул для расчета поперечной составляющей падения напряжения}

_{Вернемся к рисунку 7. Векторную величину ас можно представить гипотенузой прямоугольного треугольника acd. Катет ad мы уже вычислили. Определим поперечную составляющую cd.}

_{На рисунке видно, что cd=cf-df.}

_{Используя выведенные закономерности проведем небольшие математические преобразования и получим поперечную составляющую падения напряжения.}

_{Определение формулы для расчета напряжения U1 в начале ЛЭП}

_{Зная величину напряжения на конце линии U2, потери ∆Uл и поперечную составляющую падения δU, можно вычислить по теореме Пифагора величину вектора U1. В развернутой форме она имеет следующий вид.}

_{Расчет потерь напряжения выполняется инженерами на стадии создания проекта электрической схемы для оптимального выбора конфигурации сети и составляющих ее элементов.}

_{В процессе эксплуатации электроустановок при необходимости могут периодически проводиться одновременные замеры векторов напряжений на концам линий и сравнение полученных результатов методом простых расчетов. Этот способ актуален для устройств, к которым предъявляются повышенные требования, обусловленные необходимостью высокой точности работы.}

_{Потери напряжения во вторичных цепях}

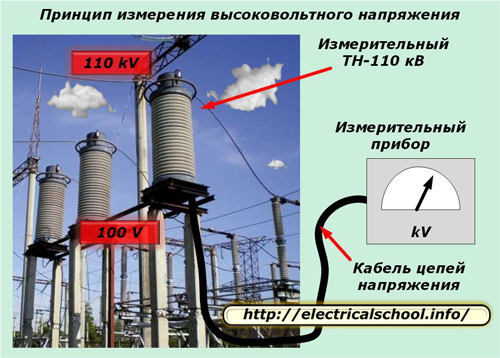
_{Примером могут служить вторичные цепи измерительных трансформаторов напряжения, которые по длине иногда достигают нескольких сотен метров и передаются специальным силовым кабелем увеличенного сечения.}

_{К электрическим характеристикам такого кабеля предъявляются повышенные требования по качеству передачи напряжения.}

_{Современные защиты электротехнических объектов требуют работу измерительных систем с высокими метрологическими показателями и классом точности 0,5 или даже 0,2. Поэтому потери подводимого к ним напряжения необходимо контролировать и учитывать. Иначе вводимая ими погрешность в работу оборудования может существенно влиять на все эксплуатационные характеристики.}

_{Потери напряжения внутри протяженных кабельных линий}

_{Особенность конструкции длинного кабеля состоит в том, что он обладает емкостным сопротивлением за счет довольно близкого расположения токопроводящих жил и тонкого слоя изоляции между ними. Оно дополнительно отклоняет проходящий через кабель вектор тока и изменяет его величину.}

_{Влияние снижения напряжения на емкостном сопротивлении необходимо учесть в расчете для изменения величины I∙z. В остальном описанная выше технология не меняется.}

_{В статье приведены примеры потерь и падения напряжения на воздушных линиях электропередач и кабелях. Однако, они происходят во всех потребителях электроэнергии, включая электродвигатели, трансформаторы, индуктивности, конденсаторные установки и другие устройства.}

_{Величина потерь напряжения для каждого вида электрооборудования законодательно регламентирована применительно к условиям эксплуатации, а принцип их определения во всех электрических схемах действует одинаково.}

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

5.3. Реактивная мощность и потеря напряжения

Рассмотрим зависимость потери напряжения в ЛЭП от мощности КБ, подключенной в ее конце.

(5.2)

Максимальное значение потери напряжения имеет место при отключенной батарее. Этот случай изображен на векторной диаграмме рис.5.2а: ток нагрузки I=Iп отстает от напряжения Uп на угол φ, вектор падения напряжения в ЛЭП ΔU почти совпадает по фазе с напряжениями Uпит и Uп, напряжение Uп по величине значительно меньше напряжения Uпит, т. е. имеет место значительная потеря напряжения.

При подключении батареи потеря напряжения в ЛЭП снижается тем больше, чем мощнее батарея. При мощности Qк , значительно превышающей Qп (режим перекомпенсации ), потеря напряжения в ЛЭП может стать отрицательной:

, , ΔU 0 по отношению к Uпит и Uп. Потеря напряжения отрицательна, т. е. напряжение Uп больше, чем Uпит. Напряжения Uпит в случаях “а” и “б” одинаковы, поэтому видно, как значительно увеличилось напряжение Uп в случае “б” за счет подключения КБ.

Рис.5.2. Векторные диаграммы напряжений в ЛЭП.

а) батарея отключена (Qк=0); б) батарея подключена, Qк › Qп.

5.4 Потребители реактивной мощности (рм)

АД – асинхронные двигатели;

Величину получаемой электроприемником РМ характеризуют cosφ и tgφ:

; ;

Реактивная мощность, потребляемая АД зависит от величины подведенного напряжения U* = U / Uн и от нагрузки на валу Кз = Р / Рн.

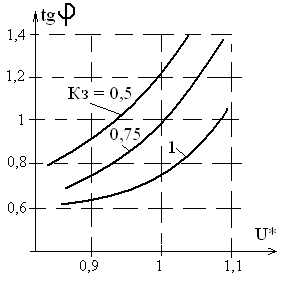
Рис. 5.3. Зависимость tgφ АД от напряжения и загрузки.

Из графиков зависимости tgφ = f(Кз, U*) видно, что tgφ, (т.е. относительное потребление РМ) минимален при высокой загрузке двигателя и пониженном напряжении на его зажимах. Он возрастает при увеличении напряжения и при снижении нагрузки. .

Статические характеристики узла нагрузки – это зависимость потребления активной и реактивной мощности в узле нагрузки от напряжения P = f(U), Q = f(U).

На рисунке 5.4. показан пример статических характеристик узла нагрузки с преимущественно асинхронной нагрузкой.

Рис. 5.4. Статические характеристиcки узла нагрузки.

5.5 Методы снижения потребляемой Р.М. (методы повышения cosφ)

Эти методы делятся на 2 группы:

а) без применения компенсирующих устройств (КУ):

— замена малозагруженных двигателей и трансформаторов на менее мощные;

— ограничение времени работы двигателей на холостом ходу;

— переключение малозагруженных двигателей с наY для уменьшения напряжения на каждой обмотке;

— применение синхронных двигателей (СД) вместо АД;

— применение схемы выходного дня в эл.сетях предприятий (большую часть из трансформаторов отключают, а их небольшую нагрузку переводят на оставшиеся в работе трансформаторы, рис.5.5).

Рис. 5.5. Схема выходного дня.

Для схемы выходного дня нужна связь по низкому напряжению между ТП посредством ЛЭП 0,4 кВ.

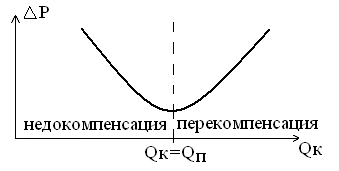
б) Применение КУ позволяет разгрузить электропередачу от РМ и снизить в ней потери активной мощности. Максимальное снижение потерь имеет место при идеальной компенсации, когда мощность КУ Qк равна потребляемой РМ Qп (рис.5.6).

Рис. 5.6. Зависимость потерь активной мощности ΔР от мощности КУ.

Дополнительное снижение потерь активной мощности ΔР происходит также благодаря увеличению напряжения U₂ на зажимах потребителя в результате компенсации РМ. Например предположим, что в электроустановке до компенсации:

После компенсации tgφ_ПК= 0,3.

а) Электроустановка питается по кабельной ЛЭП (индуктивное сопротивление мало):

_{x ≈ 0} => U_2ПК ≈U_2ДК (ПК- после компенсации, ДК- до компенсации), т.е. компенсация РМ не привела к увеличению напряжения U₂.

Потери активной мощности в сопротивлении электропередачи r:

(принято: Р = 1, U₂ = 1);

;

Благодаря компенсации РМ потери активной мощности снизились с 2r до 1,09r.

б) Электроустановка питается по воздушной ЛЭП (индуктивное сопротивление велико), компенсация РМ привела к увеличению напряжения U₂ на 5%, r = Const:

.

Увеличение напряжения U₂ на 5%, привело к дополнительному снижению на 10% потерь активной мощности в ЛЭП. Это снижение объясняется снижением тока, протекающего по ЛЭП.

Источник