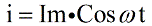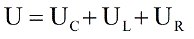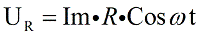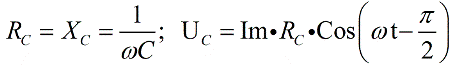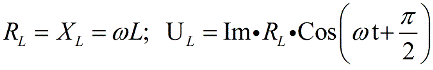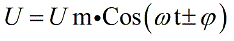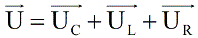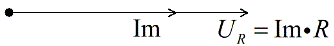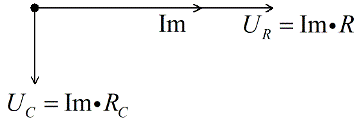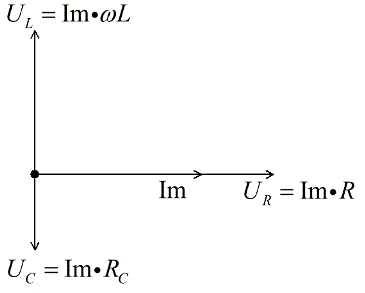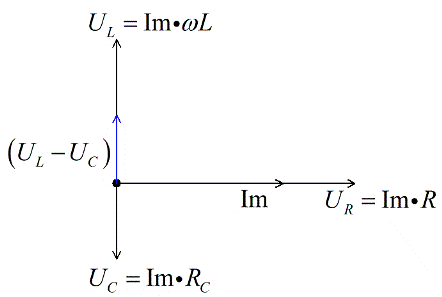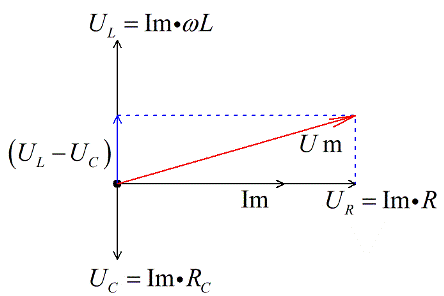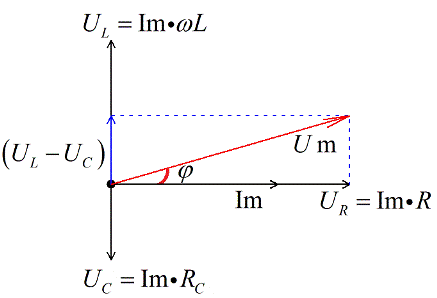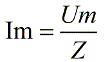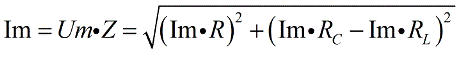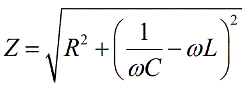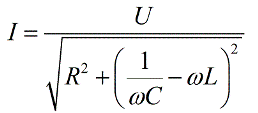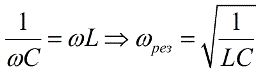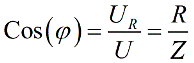Как построить векторную диаграмму токов и напряжений

Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.

В основе метода лежит тот факт, что всякую величину, меняющуюся по синусоидальному закону (смотрите — синусоидальные колебания), можно определить как проекцию на какое-то выбранное направление вектора, вращающегося вокруг своей начальной точки с угловой скоростью, равной угловой частоте колебаний изображаемой переменной величины.

Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.

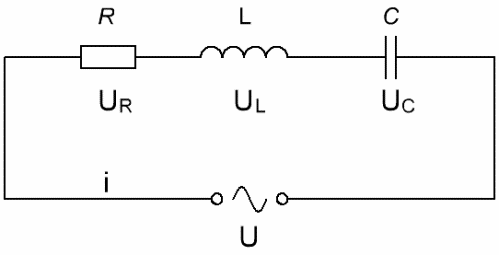
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:

Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR– на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:

Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:

А вот конденсатор в цепи переменного тока обладает реактивным емкостным сопротивлением, и напряжение на конденсаторе все время отстает по фазе от тока на Пи /2 , значит пишем:

Катушка, обладающая индуктивностью, в цепи переменного тока выступает реактивным индуктивным сопротивлением, и напряжение на катушке в любой момент времени опережает по фазе ток на Пи/ 2 , следовательно, для катушки запишем:

Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:

Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.

Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:

Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.

Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:

Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.

Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.

Напряжение на катушке опережает на Пи /2 ток, следовательно откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.

Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.

Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.

Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.

Запишем закон Ома для общего сопротивления Z (импеданса):

Из векторных изображений по Теореме Пифагора можем записать:

После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:

Тогда получим выражение для закона Ома для цепи переменного тока:

Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:

Косинус фи из наших геометрических построений получается:

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Векторная диаграмма токов и напряжений

Процессы, протекающие в электроцепи переменного тока с активным сопротивлением и реактивной индуктивностью, можно наглядно выразить в графическом виде.

Статья даст описание, что такое векторные диаграммы, где и для чего они используются. Также будет описана временная диаграмма и ее назначение. В конце будет дан пример построения простой диаграммы для электроцепи с последовательным соединением элементов.

Определение

Векторная диаграмма токов и напряжений — это геометрическое изображение всех процессов, величин и амплитуд синусоидального тока. Все имеющиеся величины располагаются на плоскости в виде векторов.

Построение векторной диаграммы использует физика и электротехника. Благодаря созданию такой диаграммы можно значительно упростить выполняемые расчеты, а так же в наглядном и доступном виде отобразить происходящие процессы.

Метод векторных диаграмм позволяет также увидеть в цепи переменного тока возникающие короткие и межфазовые замыкания, а также вычислить возможные потери мощности.

Обычно такая диаграмма строится вместе с временной. Временная диаграмма — это графическое изображение входа и выхода в электрической цепи. Временные диаграммы помогают определить временной промежуток между началом, протеканием и окончанием сигнала. Например, при нажатии на кнопку возникает сигнал, который поступает к приемнику и запускает процесс его работы.

Временные диаграммы также применимы к синусоидальной электрической цепи, так как этот ток имеет начальную точку отсчета (включение питания) и время движения от источника тока к потребителю. Такие диаграммы представляют собой график, на котором изображается начальная точка отсчета, вектор времени и углы смещения фаз.

Разновидности

Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:

1. Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
2. Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.

Векторную диаграмму токов можно построить 2 разными способами:

1. Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.
2. Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.

Построение

Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.

1. Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
2. Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
3. Напряжение резистора UR 10 вольт, его направление совпадает с током I.
4. Сила тока в цепи I равняется 3 ампера.

Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.

1. Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.
2. Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.
3. Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.
4. Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.
5. Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.

Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.

Способ 2

Построение векторных диаграмм с учетом всех известных значений для цепи переменного тока с последовательным соединением конденсатора, резистора и катушки индуктивности. При таком построении нам так же известно напряжение самой цепи. Цепь состоит из:

• Резистора UR;
• Конденсатора UC;
• Катушки UL.

1. На плоскости Im откладывается вектор UR (резистор). Его направление точно совпадает с током, поэтому это будет горизонтальная линия.
2. От точки отсчета откладывается вниз вектор UC (конденсатор). Вектор откладывается под углом 90 градусов вниз, так как он имеет указанное ранее опережение 90°.
3. От этой же точки отсчета откладывается вектор UL (катушка индуктивности). Ее значение откладывается ровно на 90 градусов вертикально, так как есть сдвиг фазы на 90 градусов.

Данная диаграмма может использоваться для контроля и расчета влияния всех известных параметров цепи и элементов, а также их взаимосвязи между собой.

1. Показать результат сложения вектора UL и UC.
2. При увеличении величины сопротивления определить разницу между напряжением и сопротивлением можно, используя новый вектор Um.
3. Кроме того можно определить угол сдвига фазы φ в цепи.

Основное преимущество векторной диаграммы заключается в следующем — простое и быстрое сложение, вычитание двух параметров во время расчета электрических цепей.

Понятие о векторах и векторных диаграммах также подразумевает расчет цепи питания трехфазной сети, подключенной по методу звезды. Она строится с учетом сразу 3 отложенных векторов от 0 оси ординат. Такое построение определяет вектор от источника тока к приемнику. Строится вектор со следующими значениями:

1. На оси ОХ откладываются настоящие значения величин, а на оси OY мнимые значения.
2. Угловая величина обозначается как W.
3. Также присутствует сам вектор Im и угол сдвига фаз φ.

1. На плоскости выбрать точку отсчета.
2. От нее отложить вектор Im, учитывая угол сдвига фаз равный 90°.
3. Длина вектора Im равна значению его напряжения и откладывается в выбранном масштабе.

Таким же образом на плоскость накладываются еще две прямые линии. Общая диаграмма покажет симметричность фаз или их сдвиг при появлении короткого замыкания. Такая диаграмма может стать примером для расчета напряжения, тока или нагрузки на каждую фазу с моделированием различных параметров.

Заключение

Векторные диаграммы сложны в понимании при расчете сложных цепей, с большим количеством сопротивлений и индуктивностью. Также, при расчете стоит учитывать тип соединения всех элементов, симметрию цепи и основные ее значения.

Видео по теме

Источник