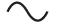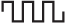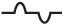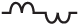Vrms что это напряжение

Параметры переменного напряжения

Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

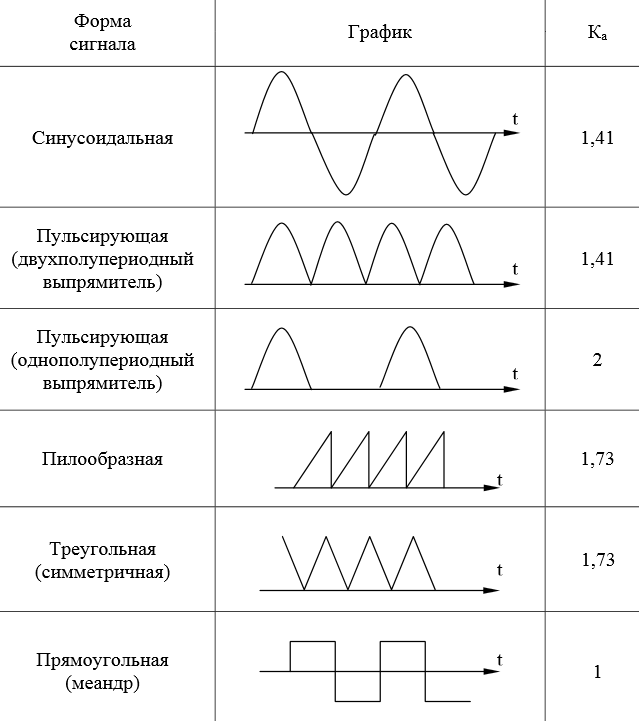
Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.

Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».

Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

среднее, среднеквадратичное и пиковое значения напряжения

• Сред. — средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ — среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. — амплитудное значение сигнала
• Пик-пик. — размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

Источник

Истинное RМS – единственно правильное измерение

Во многих коммерческих и промышленных установках происходят постоянные отключения защитных систем. Зачастую отключения кажутся случайными и необъяснимыми, но, конечно, причина существует, а в нашем случае их две. Первая возможная причина – это противотоки, которые возникают при включении некоторых видов нагрузки, например персональных компьютеров (этот вопрос будет рассмотрен в одной из будущих публикаций данного руководства). Второй возможной причиной является то, что реальный ток, протекающий по цепи, был недоизмерен, т. е. реальные значения тока выше измеренного.

Один ток – два значения. На фото показано измерение цепи с нелинейной нагрузкой с гармоническими искажениями. Показания измерителя истинного RMS (слева) правильны, а измерителя усредненных значений (справа) – на 32 % ниже.

Занижение значений измерения случается очень часто в современных установках. Но почему это происходит, если современные цифровые измерительные приборы так точны и надежны? Ответ заключается в том, что многие инструменты не подходят для измерения искаженных токов, а большинство токов в наши дни являются таковыми.

Искажения происходят из-за гармонических токов, производимых нелинейными нагрузками, особенно электронным оборудованием, таким как персональные компьютеры, флуоресцентными лампами с электронным балластом и регулируемым приводом. Процесс возникновения гармоник, а также их воздействие на электрические системы будет описываться в одной из будущих публикаций руководства (раздел 3.1). На рис. 3 изображена типичная кривая тока, потребляемого персональным компьютером. Очевидно, что это не синусоида, а стало быть все обычные синусоидные измерительные приборы и методы вычисления больше не применимы. Это означает, что при ремонте или анализе работы системы электроснабжения необходимо использовать приборы, которые могут измерять несинусоидальные токи и напряжения.

На рис. 1 изображены два измеряющих прибора (токовые клещи) на одной и той же цепи. Оба прибора работают правильно и откалиброваны по спецификациям производителя. Ключевое различие заключается в том, как измеряют данные инструменты.

Левый прибор является устройством измерения истинного RMS, а правый – это калиброванный прибор, измеряющий усредненный RMS. Для того чтобы оценить разницу, необходимо понять, что означает RMS.

Что такое RMS?

Среднеквадратичная величина (RMS) переменного тока – это величина, эквивалентная значению постоянного тока, который производил бы такое же количество теплоты при фиксированной нагрузке. Количество теплоты, производимой в резисторе переменным током, пропорционально квадрату тока, усредненного по полному циклу кривой. Другими словами, производимая теплота пропорциональна среднему значению квадрата, и, таким образом, величина тока пропорциональна корню среднеквадратичного значения (полярность не имеет значения, т. к. квадрат всегда положителен).

Типичная кривая тока, потребляемого персональным компьютером

Для правильной синусоиды (рис. 2) величина RMS составляет 0,707 от максимального значения, или максимальное значение равно √2, или 1,414, от значения RMS. То есть максимальное значение 1-амперного RMS тока чистой синусоиды будет равно 1,414 А. Если амплитуда синусоиды усредняется (с преобразованием отрицательной половины цикла), среднее значение будет равно 0,636 от максимального или 0,9 от значения RMS. На рис. 2 показаны две важных пропорции:

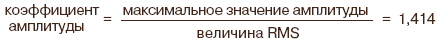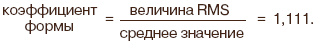При измерении правильной синусоиды (и только для правильной синусоиды) правомерно делать простое измерение среднего значения (0,636 х максимум) и умножать результат на коэффициент формы, равный 1,111 (что составит 0,707 от максимума), и назвать его RMS-величиной. Подобный подход используется в аналоговых измерительных приборах, где усреднение осуществляется путем инерции и гашения колебаний в катушке индуктивности, а также во всех старых и более современных цифровых универсальных измерительных приборах. Метод описывается как измерение, усредненное, RMS-калиброванное.

Проблема заключается в том, что этот метод работает только для правильных синусоид, которые не существуют в реальных электроустановках. Кривая на рис. 3 – это типичная кривая тока, потребляемого персональным компьютером. Точное RMS-значение все еще равно 1 А, но максимальное значение гораздо выше – 2,6 А, а среднее значение гораздо ниже – 0,55 А.

Если эта кривая измеряется усредняющим RMS-прибором, то она будет читаться как 0,61 А, в то время как реальная величина равна 1 А (т. е. почти на 40 % меньше). В таблице приведены некоторые примеры того, как два различных типа измерителей реагируют на различные формы волн.

В измерителе истинного RMS берется квадрат моментальной величины входящего тока, усредняется по времени, а затем на дисплее показывается квадратный корень от этого среднего значения. При идеальных условиях применения показания абсолютно точны, какая бы ни была кривая. Однако применение никогда не бывает идеальным, и следует принимать во внимание два ограничивающих фактора: частотную характеристику и коэффициент амплитуды.

Для функционирования систем электроснабжения обычно достаточно произвести измерения до 50-й гармоники, т. е. до частоты приблизительно в 2 500 Гц. Максимальное значение амплитуды, пропорция между максимальным значением и RMS-значением очень важны. Более высокие значения максимальной амплитуды требуют приборы с более широким динамическим диапазоном, а следовательно, более высокой точности в преобразовании диаграммы.

Несмотря на то что приборы дают различные показания при измерени искаженных кривых, показания обоих приборов совпадут при измерении правильной синусоиды. Это условие, при котором они калибруются, т. е. каждый тип измерительного прибора может быть сертифицирован как калиброванный, но только для использования на синусоидах.

Счетчики истинного RMS появились по крайней мере 30 лет назад, но они были специализированными и относительно дорогими приборами. Достижения в электронике привели к тому, что функции истинного RMS-измерения встраиваются во многие переносные мультиметры. К сожалению, эта техническая характеристика встречается только в наиболее современных продуктах большинства производителей, но при этом они не так дороги, как раньше, и стали доступными инструментами для использования в повседневной деятельности.

Таблица Сравнение реакций на различные формы волн измерителей усредненного и истинного RMS

Тип измерения мультиметра Реакция на синусоиду Реакция на прямоуголь- ное колебание Реакция на однофазный диодный выпрямитель Реакция на трехфазный диодный выпрямитель Усредненное RMS Правильная На 10 % выше На 40 % ниже На 5–30 % ниже Истинное RMS Правильная Правильная Правильная Правильная

Последствия заниженного замера

Эксплуатационные ограничения большинства элементов электрической цепи определяются количеством тепла, которое может быть рассеяно с тем, чтобы элемент или компонент не перегрелся.

Номиналы допустимых значений тока для кабелей, к примеру, приводятся для определенных условий эксплуатации (фактор, определяющий, насколько быстро может происходить отвод тепла) и максимальной допустимой рабочей температуры. Так как гармонически загрязненные токи имеют большее значение RMS, чем то, которое замеряется счетчиком усредненного RMS, примененные провода и кабели могут иметь недостаточные номиналы и будут работать более нагретыми, чем ожидалось. Результатом будет разрушение изоляции, преждевременный износ и опасность пожара.

Размерность шины измеряется путем подсчета соотношения скорости охлаждения конвекцией и излучения, а также скорости нагрева из-за потерь сопротивления. Температура, при которой эти скорости равны, является рабочей температурой шины, или она спроектирована так, чтобы рабочая температура была достаточно низкой для избежания преждевременного износа изоляционных и опорных материалов. Как и в случае с кабелями, ошибки при измерении истинного RMS-значения приведут к более высоким рабочим температурам. Вследствие того что шины обычно имеют значительные размеры, поверхностный эффект более очевиден, чем в маленьких проводниках.

Это приводит к еще большему увеличению температуры.

Другие компоненты электрической системы, такие как плавкие предохранители и тепловые элементы автоматов отключения оцениваются в токе RMS, потому что их характеристики имеют отношение к рассеиванию теплоты. Это является основной причиной раздражающих псевдоаварийных отключений – сила тока выше ожидаемой, поэтому автомат отключения функционирует в температурном режиме, при котором отключения будут происходить неминуемо. Как при любом перерыве в подаче электроэнергии, стоимость сбоя из-за аварийного отключения может быть довольно высокой и повлечь за собой потерю данных в компьютерных системах, сбои в работе систем управления технологическими процессами и т. д. Эти вопросы будут обсуждаться в будущих публикациях руководства (раздел 2)

Таким образом, только с помощью инструментов измерения истинного RMS возможен точный выбор номиналов кабелей, шин, фидеров и защитной аппаратуры. Важным является вопрос, является ли данное устройство прибором измерения истинного RMS? Обычно, если счетчик является измерителем истинного RMS, это указывается в спецификации продукта. Практически ответ может быть получен путем сравнения показаний известного усредняющего измерителя (как правило, самого дешевого, который может быть в распоряжении) и предполагаемого измерителя истинного RMS при замере тока в нелинейной нагрузке, например, тока от персонального компьютера с током лампы накаливания. Оба измерителя покажут одинаковую силу тока для нагрузки лампы накаливания. Если один из приборов имеет значительно более высокие показатели (скажем на 20 % выше) для нагрузки персонального компьютера, чем для другой нагрузки, тогда, вероятно, он является прибором истинного RMS, а если показания одинаковы – приборы относятся к одному и тому же типу.

Заключение

RMS-замеры важны для любой установки, в которой имеется значительное число нелинейных нагрузок (персональные компьютеры, электронные балласты, компактные флуоресцентные лампы и т. д.). Усредняющие RMS-измерители дают недомер до 40 %, что приводит к недооценке номиналов кабелей и защитных устройств. Это грозит сбоями в их работе, аварийными отключениями и преждевременным износом.

Нелишне помнить и о том, что при функционировании в режимах нерасчетной электрической и, главное, тепловой нагрузки, вызванной недооценкой истинных значений токов в результате недомера, снижается общая энергоэффективность электроустановки.

Перепечатано с сокращениями из издания Европейского института меди

«Прикладное руководство по качеству электроэнергии»

Источник