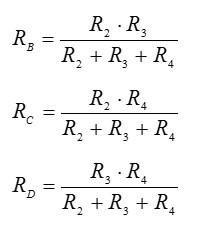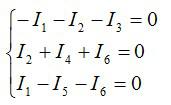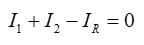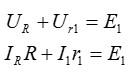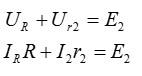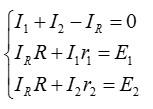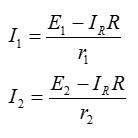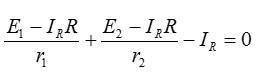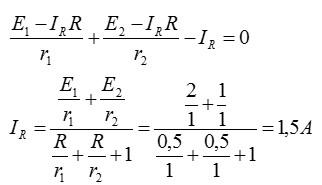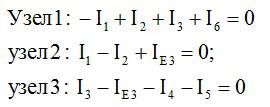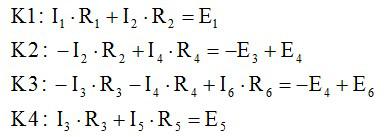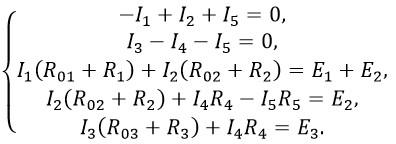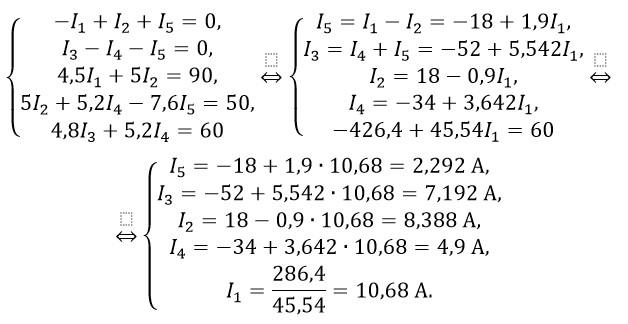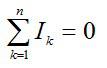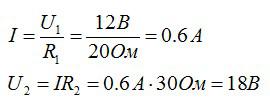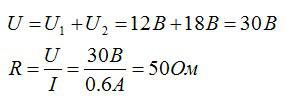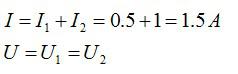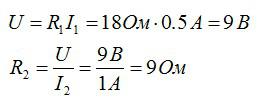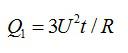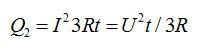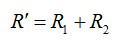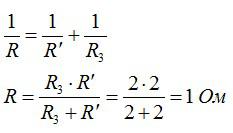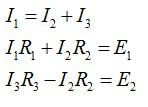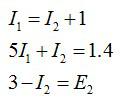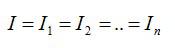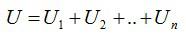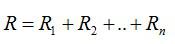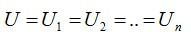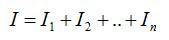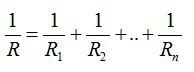Задача два источника напряжения

Электрическая цепь с двумя источниками

Электрическая цепь может содержать несколько источников или приемников электроэнергии. Такие цепи называются сложными, для расчетов основных величин в таких цепях применяют специальные методы.

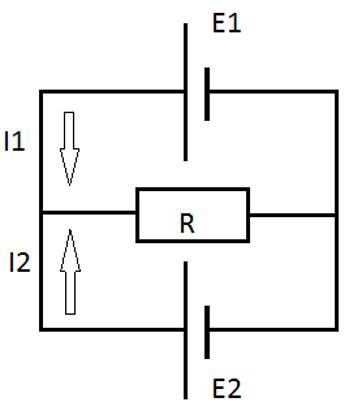
На рисунке 1 приведена схема с двумя источниками ЭДС: E₁ и E₂. Источники имеют внутренние сопротивления r₁ и r₂. Нагрузка условно обозначена резистором с сопротивлением R. Так как в цепи отсутствуют разветвления, то ток во всех ветвях будет одинаков и равен I

Рис. 1. Схема электрической цепи с двумя источниками ЭДС

Для расчета сложных электрических цепей наряду с законом Ома применяются два закона Кирхгофа.

Одним из наиболее простых способов расчета цепи с двумя источниками ЭДС является метод наложения токов. Данный метод основан на аддитивном свойстве токов, согласно которому ток в цепи равен алгебраической сумме токов, создаваемых каждым источником питания независимо друг от друга. Это правило применимо для расчета любой линейной цепи (то есть цепи, в которой сопротивления всех участков постоянны).

Пусть в электрической цепи действует только один источник ЭДС E₁, тогда ток в цепи будет равен

Теперь положим обратную ситуацию: в электрической цепи действует только один источник ЭДС E₂, а источник E₁ присутствует, но не производит ток. Тогда ток в цепи будет равен

Два источника ЭДС в цепи направлены встречно, следовательно, суммарный ток I будет равен разности токов I₁ и I₂

Из свойства аддитивности токов можно сделать немаловажный вывод: если ЭДС E₁ и E₂ имеют встречное направление, и равны, то ток в цепи будет равен нулю

Если значения E₁ и E₂ различны, то в цепи возникает ток, направление которого совпадает с током, создаваемой «большим» ЭДС. Иными словами, если E₁ > E₂, то направление тока совпадает с ЭДС E₁, если E₁ E₂).

Электродвижущая сила E₂, направленная в противоположную току I сторону, называется встречной или противо-ЭДС.

Рассмотрим процессы и запишем основные зависимости, которые соответствуют каждому из участков цепи.

На участке ab имеется сопротивление источника ЭДС r₁, а действие самого источника совпадает с направлением тока I. Следовательно указанный источник работает в режиме генератора (источника энергии). Таким образом, ЭДС источника равна сумме напряжения на его выводах и внутреннего падения напряжения

Согласно записанному выше выражению,

Иными словами, напряжение на выводах источника, отдающего энергию в цепь, равно разности ЭДС источника и внутреннего падения напряжения.

Согласно закону Ома, на участке bc падение напряжения равно

Кроме того, следует отметить, что на участке bc электрическая энергия преобразуется в тепловую, при этом происходит выделение мощности, равной

На последнем рассматриваемом участке ca источник ЭДС E₂ действует против направления тока I. Источник имеет сопротивление r₂. На данном участке имеется потеря мощности (нагрев), равная r₂ ⋅ I 2 . Кроме того, источник ЭДС создает собственную мощность E₂⋅ I, направленную на преодоление сил встречной ЭДС. Получается, что источник с противо-ЭДС работает в цепи как потребитель (приемник).

Мощность, выделяемая на участке ca равна

Cледовательно, напряжение на этом участке равно

На основании записанного выше выражения можно сделать вывод, что напряжение на вывод источника, работающего в режиме противо-ЭДС равно сумме самого ЭДС и внутреннего падения напряжения на нем.

Источник

Задачи на правило Кирхгофа с решением

Мы уже писали про закон Ома, а также параллельное и последовательное соединение проводников. Но это были цветочки. Сегодня разберемся с задачами посложнее: посмотрим, как решаются задачи на правила Кирхгофа.

Не забывайте подписаться на наш телеграм-канал: там вас ждут актуальные новости сферы образования, полезные лайфхаки и скидки для студентов.

Задачи на правило Кирхгофа с решением

Как решать задачи по правилу Кирхгофа? Прежде, чем приступать к решению задач, обязательно изучите теорию. Также мы подготовили для вас универсальную памятку по решению физических задач.

Задача №1 на эквивалентные преобразования соединений проводников.

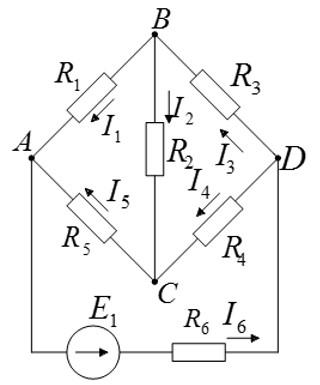
Преобразуйте схему с помощью эквивалентных преобразований.

Кроме основных формул для последовательного и параллельного соединения проводников, существуют формулы для преобразования звезды резисторов в эквивалентный треугольник и наоборот. Треугольник резисторов R2 R3 R4 можно преобразовать в эквивалентную звезду RB RB RD по формулам:

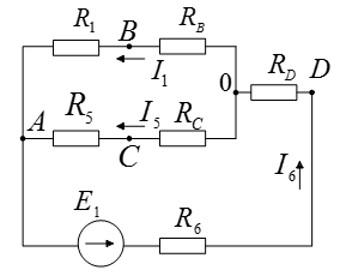
Преобразованная схема будет выглядеть следующим образом:

Ответ: см. выше.

Правила Кирхгофа применяются для сложных цепей(например, для цепей с несколькими источниками питания), когда эквивалентные преобразования не приносят результата.

Задача №2 на первое правило (закон) Кирхгофа

Необходимо составить уравнения по первому закону Кирхгофа для следующей цепи:

В данной цепи 4 узла. По первому закону составляем 3 уравнения (на 1 уравнение меньше, чем количества узлов):

Ответ: см. выше.

Для решения задач на правила Кирхгофа необходимо уметь решать системы линейных уравнений. Для решения сложных систем удобно использовать специальные программы: MathCad, MatLab и т.д.

Далее для наглядности рассмотрим задачу с более простой схемой.

Задача №3 на правила Кирхгофа

Два источника питания E1=2В и E2=1В соединены по схеме, показанной на рисунке. Сопротивление R=5 Ом. Внутреннее сопротивление источников одинаково и равно r1=r2=1 Ом. Определить силу тока, который проходит через сопротивление.

По первому закону Кирхгофа сумма токов, сходящихся в узле, равна нулю (токи обозначим произвольно):

Выберем направление обхода верхнего контура против часовой стрелки. По второму закону Кирхгофа, сумма падений напряжений в контуре равна сумме ЭДС:

Запишем то же самое для второго контура, обходя его по часовой стрелке:

Объединим уравнения с неизвестными токами в систему:

Чтобы решить систему, выразим силу тока I1 из второго уравнения, а силу тока I2 – из третьего:

Первое уравнение теперь можно записать в виде:

Выражая искомый ток и подставляя значения из условия, получаем:

Ответ: 1,5 А.

Задача №4 на правила Кирхгофа

Дана схема электрической цепи. Необходимо:

• обозначить сопротивления, над каждой ветвью указать свой ток и источники ЭДС;
• указать на схеме направления токов и ЭДС;
• составить уравнения по первому и второму закону Кирхгофа.

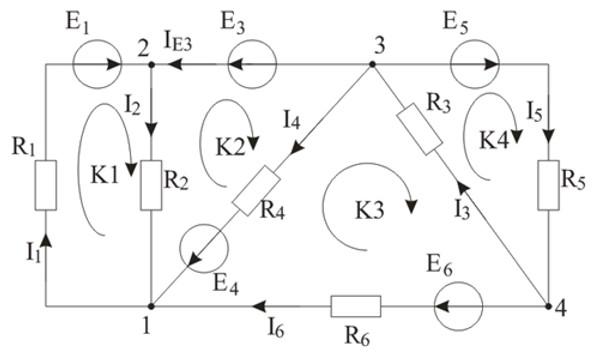
Приведем схему, обозначив сопротивления, ЭДС и токи:

В схеме 7 токов и 4 узла. Необходимо составить 4 – 1 = 3 уравнения по первому закону Кирхгофа и 7 – 3 = 4 уравнения по второму закону Кирхгофа.

Второй закон Кирхгофа (выбранные контуры К1, К2, К3, К4 указаны на рисунке):

Ответ: см. выше.

Задача №5 на правила Кирхнофа

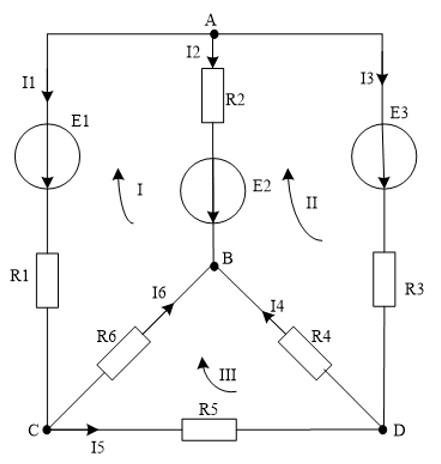
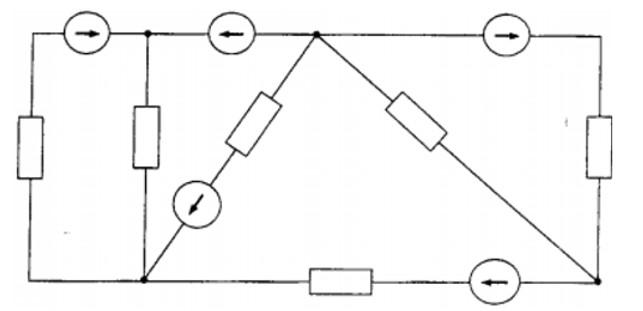
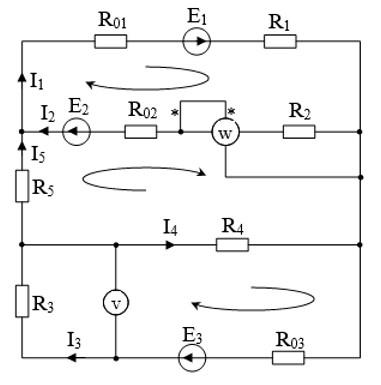
Определить все токи в ветвях, составив систему уравнений по законам Кирхгофа.

Параметры цепи: E1 = 40 В, E2 = 50 В, E3 = 60 В, R01 = 0,1 Ом, R02 = 0,3 Ом, R03 = 0,2 Ом, R1 = 4,4 Ом, R2 = 4,7 Ом, R3 = 4,6 Ом, R4 = 5,2 Ом, R5 = 7,6 Ом.

Направления токов в ветвях цепи и направления обхода контуров указаны на схеме. Цепь содержит 3 узла и 3 независимых контура. Таким образом, для расчета токов в ветвях необходимо составить два уравнения по первому закону Кирхгофа и три по второму:

Подставим числовые значения и решим систему уравнений:

Ответ: I1=10,68 А; I2=8,388 А; I3=7,192 А; I4=4,9 А; I5=2,292 А.

Вопросы на правила Кирхгофа

Вопрос 1. Сформулируйте первый закон Кирхгофа.

Ответ. Первый закон Кирхгофа связан с сохранением заряда и формулируется следующим образом:

Для любого узла электрической цепи алгебраическая сумма токов ветвей, подключенных к данному узлу, равна нулю.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда, согласно которому ни в какой точке заряды не могут безгранично накапливаться: количество электричества, притекающее к данной точке за определенный промежуток времени, должно быть равно количеству электричества, оттекающему от неё.

Вопрос 2. Как следует выбирать направления токов в ветвях электрической цепи?

Ответ. Направления токов во всех ветвях электрической цепи задаются произвольно до составления уравнений. Токи, входящие в узел, принято считать положительными, а выходящие из узла – отрицательными.

Вопрос 3. Как формулируется второй закон Кирхгофа?

Ответ. Второй закон Кирхгофа связан с законом сохранения энергии и формулируется следующим образом:

Алгебраическая сумма всех ЭДС контура электрической цепи равна алгебраической сумме напряжений и алгебраической сумме падений напряжений на всех его участках.

Вопрос 4. Что следует учитывать при составлении уравнений второго закона Кирхгофа для цепи и ее конкретного контура.

Ответ. Перед составлением уравнений второго закона Кирхгофа для цепи необходимо произвольно выбрать направления токов во всех ветвях цепи и определить направление обхода контура.

При составлении уравнения для конкретного контура учитываются:

• токи, входящие в узлы принимаются положительными;
• ЭДС источников принимаются положительными, если
• направления их действия (стрелка) совпадает с выбранным направлением обхода (независимо от направления тока в них);
• падения напряжений в ветвях (IkRk) принимаются положительными, если положительное направление тока совпадает с выбранным направлением обхода;
• напряжения Uk, включенные в контур, принимаются положительными, если эти напряжения создают ток, направленный также как и направление обхода (направление напряжения, определяемое стрелкой, совпадает с направлением обхода).

Вопрос 5. Что такое эквивалентные преобразования последовательного и параллельного соединения пассивных элементов?

Ответ. Задачей эквивалентного преобразования последовательного и параллельного соединения пассивных элементов, является последовательное упрощение исходной схемы и нахождение эквивалентного сопротивления схемы.

Нужна помощь в решении задач и других студенческих заданий? Профессиональный сервис помощи учащимся окажет оперативную помощь с выполнением любой работы.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Задачи на параллельное и последовательное соединение проводников с подробными решениями

Что бы ни происходило в мире, учиться надо всегда. Кстати, для тех, кто не знает, как организовать учебу на удаленке, мы подготовили отдельную статью. А сегодня займемся решением задач на последовательное и параллельное соеднинение проводников. Решение задач – отличный способ, чтобы успокоить нервы и не поддаваться панике.

Присоединяйтесь к нам в телеграме: там вас ждут актуальные новости и приятные скидки.

Последовательное и параллельное соединение проводников: решение задач

Как решать задачи с параллельным и последовательным соединением проводников? Для начала повторите теорию, вспомните общую памятку по решению физических задач и на всякий случай держите под рукой формулы.

Задача №1 на последовательное соединение проводников

Проводники сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника равно 12 В. Определите напряжение, сопротивление и силу тока в цепи на втором проводнике, а также полное напряжение.

Для последовательного соединения проводников:

Ответ: 50 Ом; 18 В; 0,6 А; 30 В.

Задача №2 на параллельное соединение проводников

Два проводника соединены параллельно. Сила тока в первом проводнике равна 0,5 А, во втором — 1 А. Сопротивление первого проводника составляет 18 Ом. Определите сопротивление второго проводника и силу тока на всем участке цепи.

Для параллельного соединения:

При решении задач не забывайте проверять размерности величин и при необходимости переводить их в систему СИ.

Ответ: 1,5 А; 9 Ом.

Задача №3 на последовательное и параллельное соединение проводников

Электрогрелка состоит из трех одинаковых секций. Во сколько раз быстрее грелка будет нагревать некоторое количество воды от 10 до 100 градусов Цельсия при параллельном включении всех секций, нежели при последовательном их включении?

Пусть сопротивление каждой секции равно R. Тогда при параллельном включении их в сеть напряжение на каждой секции равно напряжению в сети (U), и на трех секциях будет выделяться тепло:

При последовательном соединении суммарное сопротивление цепи равно 3R, а выделяющееся количество теплоты:

Как видим, выделяющееся тепло для первой схемы в 9 раз больше, так что и скорость нагрева воды будет в 9 раз выше.

Ответ: в 9 раз.

Задача №4 на смешанное соединение проводников

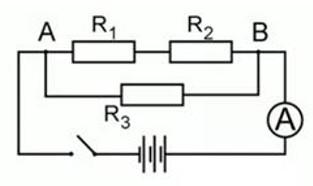
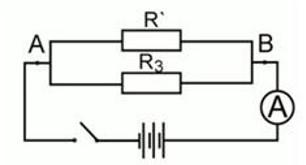
Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Определите силу тока во всей электрической цепи.

Согласно схеме, искомая сила тока – это сила тока, протекающая через амперметр.

Резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним.

Резисторы 1 и 2 можно заменить эквивалентным сопротивлением R со штрихом и перерисовать схему в упрощенном виде:

Сопротивления R3 и R со штрихом соединены параллельно, можно найти общее сопротивление электрической цепи по формуле для параллельного соединения:

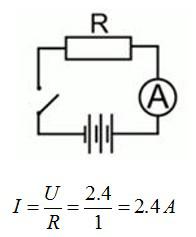
Теперь цепь можно перерисовать в еще более упрощенном виде и рассчитать силу тока по закону Ома:

Ответ: 2.4 А.

Задача №5 на закон Кирхгофа

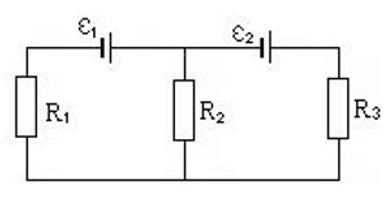
Три сопротивления R1 = 5 Ом, R2 = 1 Ом, R3 = 3 Ом и два источника тока соединены так, как показано на рисунке. Внутренними сопротивлениями источников тока можно пренебречь. ЭДС первого источника тока равна 1,4 В, и сила тока, текущего через сопротивление R3, равна I3= 1 А. Определите ЭДС второго источника тока.

Выберем направление обхода контуров по часовой стрелке и запишем закон Кирхгофа для точки A (расположим ее между двумя источниками и сопротивлением R2) и двух контуров:

Решая систему уравнений, получаем ответ: Е2=3.6 В.

Ответ: 3.6 В.

Вопросы на параллельное и последовательное соединение проводников

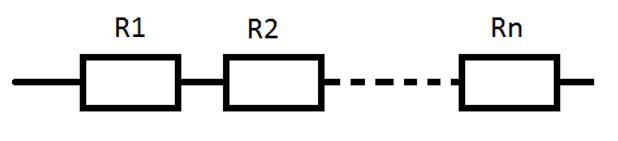
Вопрос 1. Схематически изобразите последовательное соединение проводников

Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:

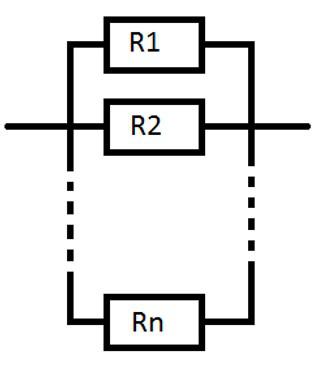
Вопрос 2. Схематически изобразите параллельное соединение проводников

Ответ. На рисунке ниже изображено параллельное соединение проводников:

Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.

Ответ. При последовательном соединении:

Сила тока во всех проводниках одинакова.

Общее напряжение равно сумме напряжений на каждом проводнике.

Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.

Ответ. Для параллельного соединения проводников:

Напряжение на всех проводниках одинаково.

Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.

Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?

Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.

Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник