Закон гука для напряжения в грунтах

Лекция 3. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ГРУНТЕ ФАЗЫ ДЕФОРМАЦИЙ ГРУНТА ПОД ФУНДАМЕНТОМ

Скачать:

в рамках общей темы «Напряженное состояние грунтов в допредельном и предельном состояниях»

Решение задачи определения напряжений в грунте необходимо для установления условий прочности и устойчивости грунтов и определения их деформаций (например, осадок). При решении вопроса о распределении напряжений в грунтах в Механике грунтов применяют теорию линейно-деформируемых тел. То есть для определения напряжений могут быть применены уравнения и зависимости теории упругости, базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука). Однако при применении закона Гука для грунтов необходимо условиться об ограничениях, поскольку в грунтах возникают не только упругие, но значительные остаточные деформации.

ОБЩАЯ ЗАВИСИМОСТЬ МЕЖДУ ДЕФОРМАЦИЯМИ И НАПРЯЖЕНИЯМИ. ПРИНЦИП ЛИНЕЙНОЙ ДЕФОРМИРУЕМОСТИ

В основу теории распределения напряжений в грунтах кладётся зависимость между относительными деформациями ε и нормальными напряжениями.

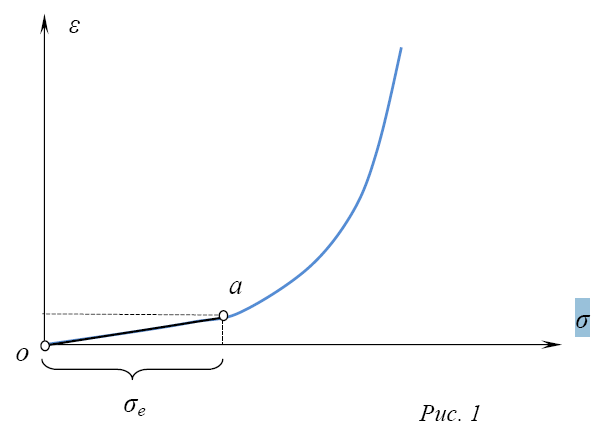
В общем случае (согласно опытам) зависимость между деформациями и напряжениями для грунтов будет нелинейной: σ

Однако в определенном интервале напряжений (при не очень больших изменениях внешних давлений – порядка 1÷3 кг/см 2 ) с достаточной для практических целей точностью зависимость между деформациями ε и нормальными напряжениями σ может приниматься линейной (спрямлённый участок оа на кривой, рис. 1).

Сформулируем принцип линейной деформируемости для грунтов: при небольших изменениях давлений грунты можно рассматривать как линейно-деформируемые тела, то есть зависимость между общими деформациями и напряжениями для грунтов может быть принята линейной: σ = Е · ε.

НАПРЯЖЕНИЕ, ПЕРЕДАВАЕМОЕ ГРУНТУ ПО ПОДОШВЕ ФУНДАМЕНТА

Это напряжение не остается по глубине постоянным, а в некоторой области грунтовой толщи рассеивается. Для решения задач о распределении напряжений применяют уравнения теории упругости, рассматривая грунты как тела однородные, изотропные и линейно-деформируемые, подчиняющиеся закону Гука. Для оснований гражданских и промышленных зданий назначают такую величину допустимых напряжений, при которой в грунте не возникают пластические (остаточные) деформации.

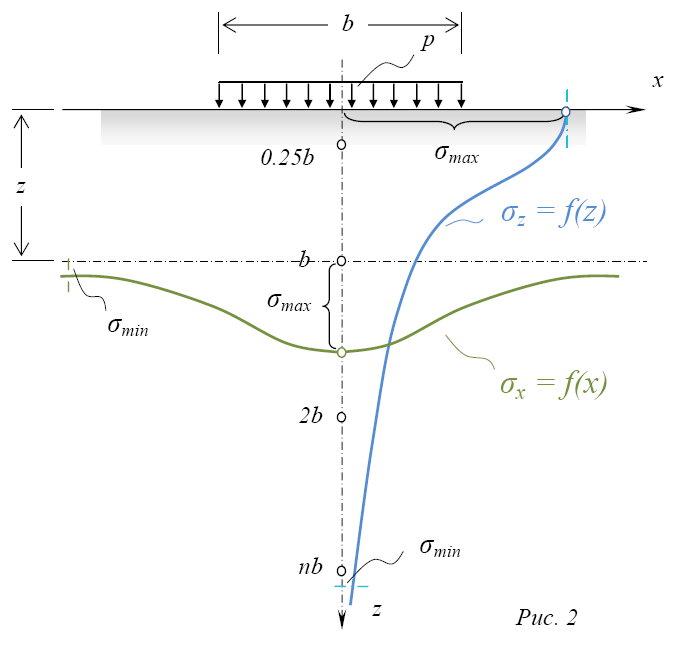
Изменение напряжений σ по различным вертикальным (z) и горизонтальным (x) сечениям характеризуется эпюрами σ_z и σ_x (рис. 2). Как видно из рисунка, напряжения в грунтовой толще изменяются, как непрерывные функции от σ_max до σ_min как по вертикальному, так и по горизонтальному направлению.

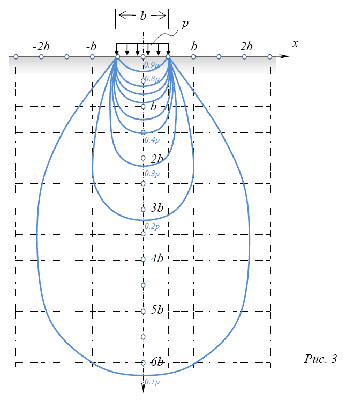
В напряженной зоне грунта имеются точки с одинаковыми напряжениями, через которые можно провести линии (т.н. кривые равных напряжений). Например, линии, проходящие через точки с одинаковым вертикальным напряжением σ_z, называются изобарами. В сжимаемой толще можно провести какое угодно число изобар (в зависимости от того, какие по величине напряжения соединяются линиями). Например, если к поверхности грунта приложена распределенная полосовая нагрузка интенсивностью p, то семейство изобар будет выглядеть следующим образом:

Семейство изобар принято называть «луковицей напряжений». Построение «луковиц напряжений» полезно при оценке напряженного состояния в основаниях сооружений: подобное изображение наглядно иллюстрирует изменение напряжений в грунте под нагрузкой.

ФАЗЫ ДЕФОРМАЦИЙ ГРУНТА ПОД ФУНДАМЕНТОМ

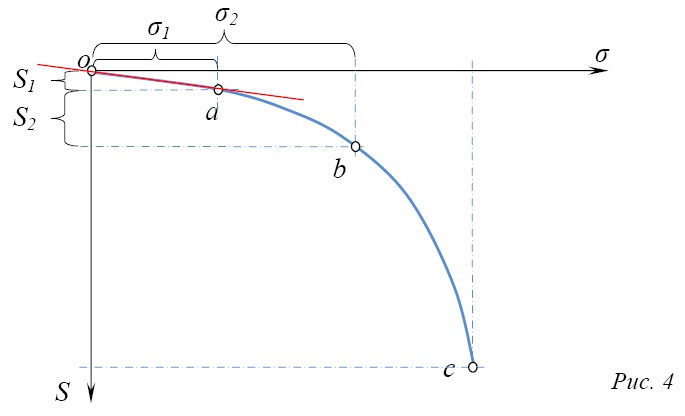
Закономерность нарастания осадок с постепенным увеличением статической нагрузки характеризуется графиком:

Этот график имеет три характерных участка (oa, ab и bc на графике, рис. 4).

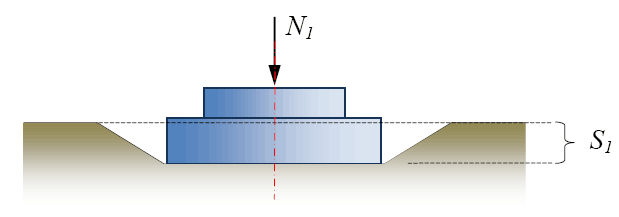
Начальный участок о имеет пологое очертание и согласно принципу линейной деформируемости может быть заменён прямой. Деформация на участке прямой называется фазой уплотнения (рис. 5).

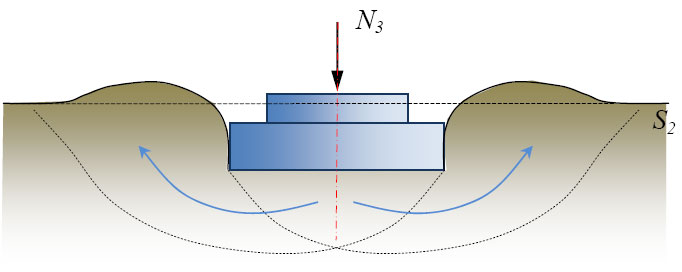
В фазе уплотнения происходит более плотная укладка частиц грунта за счёт уменьшения объёма пор. Ни в одной точке основания касательные напряжения по своей величине не превосходят сил внутреннего сопротивления грунта сдвигу, то есть повсюду существует состояние устойчивого равновесия грунта (τ τ_пр) и выпирания его из-под фундамента. Деформация на участке bc называется фазой выпирания (рис. 7).

Таким образом, при возрастании нагрузки на грунт необходимо различать две характерные её величины, при достижении которых резко меняется поведение грунта:
— первую, соответствующую началу перехода фазы уплотнения в фазу сдвигов – то есть фазу зарождения и развития зон предельного напряженного состояния;
— и вторую, когда исчерпывается несущая способность грунтового основания и наблюдается полное развитие зон предельного равновесия, при котором даже весьма незначительное увеличение нагрузки приводит грунт к потере прочности и устойчивости (к разрушению).

Источник

Деформации и напряжения в горных породах. Закон Гука

Горные породы, слагающие земную кору, являются продуктами дезинтеграции и переотложения преимущественно магматических пород, вынесенных на поверхность вулканизмом. Наряду с неизмененными магмами низы земной коры состоят преимущественно из метаморфических пород. Верхнюю часть разреза повсеместно, кроме докембрийских щитов, слагают осадочные породы различной мощности и происхождения. Средняя толщина земной коры составляет около 33 км. Под подошвой коры залегает малоизмененное первичное планетное вещество мантии – так называемое протовещество.

Породы, слагающие земную кору, и вещество глубоких недр планеты обладают различными упругими свойствами, обусловленными их различным петрографическим составом и термодинамическими условиями залегания. Под упругими свойствами понимается сопротивление среды изменению объема и формы пород под действием внешней силы.

Деформация породы происходит вследствие смещения атомов, молекул или ионов узлов кристаллической решетки вещества (жидкого, твердого или газообразного) от положения их равновесия. Внутренние силы взаимодействия между указанными компонентами вещества препятствуют этой деформации и стремятся вернуть смещенные атомы, молекулы или ионы в положение равновесия. В результате этого в породе возникают колебания частиц. Эти колебания распространяются на соседние объемы пород и таким образом происходит образование и распространение упругих колебаний (сейсмических волн) во все стороны от приложенной силы. В качестве таковой может выступать землетрясение, ядерные или обычные (тротиловые) взрывы и тому подобное. Способность пород передавать на большие расстояния с определенной скоростью упругие деформации определяет основы сейсмометрии земной коры и глубоких недр планеты, недоступных прямым наблюдениям.

Рассмотрим воздействие внешних сил на горную породу. Обозначим через s напряжение, т.е. поверхностную плотность силы, возникающую в некотором элементарном объеме тела.

В твердой, лишенной пор породе напряжение определяется выражением:

где S – площадь, на которую воздействует сила F. В обычной пористой породе площадь S состоит из площади контакта S₀ минеральных зерен и S_п – площади пор:

В поровом пространстве напряжений нет, т.е. напряжение возникает только на контактах минеральных зерен:

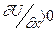
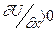
где r – плотность, г/см 3 , с – скорость упругих волн м/с. Величина , когда под влиянием внешней силы s_x частицы среды сближаются, т.е. происходит сжатие среды. При частицы среды отходят друг от друга и возникает растяжение.

Поскольку величина s_x представляет собой давление Р, то закон Гука позволяет рассчитать акустическое давление в любой точке среды.

Рис. 56. Деформации объема среды при движении P-волн (а); деформации сдвига при движении S-волн (б)

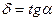
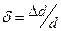
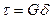
Если деформация вызывает касательное напряжение (см. рис. 56), то она определяется углом сдвига a или деформацией сдвига d, где , или :

. (VIII.7)

Здесь G – модуль сдвига. Это закон Гука для сдвиговых деформаций, или деформаций формы.

Закон Гука в своей линейной части (см. рис. 57) характеризует область упругой деформации, происходящей в малом отрезке времени (доли секунды). Однако упругое тело Гука в геологическом масштабе времени (тысячи, миллионы лет) может вести себя как пластичное тело, т.е. подчиняться нелиней­ным законам Максвелла. Такую среду называют телом Максвелла. В общем случае деформация в твердых породах слагается из упругой f₁(s) и пластичной f₂(s,t), т.е.:

Рис. 57. К иллюстрации закона Гука: ОА – область упругой деформации; АВ –область пластичной деформации

Таким образом, горные породы в разных временных масштабах могут одновременно рассматриваться и как упругие тела Гука, и как пластичные тела Максвелла. Если величина деформации превышает пределы прочности пород, то наступает их разрушение. Величина таких деформаций слишком велика и выходит далеко за пределы условий возбуждения малых (гармонических) колебаний. Поэтому мы их здесь не будем рассматривать.

Модуль Юнга Е и модуль сдвига G являются основными упругими характеристиками среды. Их размерность – кг/см 2 или н/м 2 (СИ). Для оценки отношения между продольными (DU/U) и поперечными (Dd/d) деформациями вводится коэффициент Пуассона (безразмерная величина):

. (VIII.9)

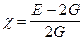
Весьма важно отметить, что через модуль Юнга и модуль сдвига можно определить скорость распространения упругих волн – объемных, называемых продольными волнами с_р – и сдвиговых волн, называемых поперечными волнами – с_s:

(м/с); (м/с), (VIII.10)

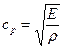
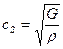
Существует весьма важное соотношение скорости продольных волн к скорости поперечных – с_р/с_s, которое является, по существу, функцией коэффициента Пуассона:

. (VIII.11)

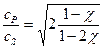
Для осадочных пород, вследствие низкого сопротивления сдвигу рыхлых отложений, величина с_р/с_s может достигать больших значений:

Для кристаллических магматических и метаморфических пород это соотношение лежит в более узких пределах:

Из приведенного видно, что скорость упругих волн в породах зависит главным образом от их плотности и практически не зависит от частоты колебаний. Последняя оказывает сильное влияние на поглощение волн.

Источник

Сжимаемость грунтов(компрессионная зависимость при объемном сжатии). Закон Гука в главных нормальных напряжениях

Страницы работы

Фрагмент текста работы

65.Сжимаемость грунтов(компрессионная зависимость при объемном сжатии)

При проведении компрессионных испытаний в одометрах образец грунта, находясь в жестком кольце, не может расширяться в стороны. В этом случае он оказывает на стенки кольца горизонтальные давления, которые соответствуют горизонтальным напряжениям σ_х, σ_у , развивающимся в образце (следовательно, σ_х= σ_у ). Вертикальное же нормальное напряжение σ_z равно интенсивности р приложенного давления Л (σ_z =р). Поскольку боковое расширение грунта отсутствует, относительные горизонтальные деформации е_х = e_v = 0.

Известно, что относительная деформация упругого тела в соответствии с законом Гука находится из выражения

E_m—модуль упругости материала

v_m-коэффициент бокового расширения материала( коэфф. Пуассона)

Так как в пределах небольших изменений давления грунты можно рассматривать как линейно-деформируемые тела, аналогичное (3.8) выражение можно написать и для зависимости между напряжениями и деформациями грунта в одометре (при сжатии образца грунта без возможности бокового расширения).

где E ₀ — модуль деформации грунта: v—коэффициент бокового расширения грунта (коэффициент Пуассона).

Подставив в выражение (3.8′) σ_х = σ_у, σ_z = р, e_x = 0 и проведя преобразования, получим

σ_х= σ_у =[v/(l-v)]р = ξ р, (3.9)

где ξ — коэффициент бокового давления грунта в состоянии покоя, т.е. при отсутствии горизонтальных перемещений.

Следовательно, изменение коэффициента пористости грунтовой массы в рассматриваемой точке основания может иметь место лишь при изменении суммы главных напряжений θ в этой точке.

67.Запишите закон Гука в главных нормальных напряжениях. Сколько независимых характеристик сжимаемости вы знаете.

68.Что такое структурная прочность грунта

Грунт, не обладающий структурной прочностью – уплотняющегийся даже под действием небольшого давления. Это обычно свойственно очень слабым глинистым грунтам и пескам. Грунты природного сложения уплотнены давлением вышележащих слоев грунта, действием капиллярного давления, развивающегося при высыхании водонасыщенного грунта и вследствие понижения уровня подземных вод (снятия взвешивающего действия воды). В результате уплотнения грунта его частицы сблизились и между ними образовались водно-коллоидные связи. При определенных условиях в них дополнительно могли возникнуть хрупкие кристаллизационные связи. Суммарно эти связи придают грунту некоторую прочность, которую и называют структурной прочностью грунта p_slr. При давлении р p_slrпроисходит уплотнение грунта. Компрессионная кривая для таких грунтов имеет вид, показанный на рис

69.Что называется коэфф. Пуассона

v-коэффициент бокового расширения грунта

70.Что называется коэфф. бокового давления грунта, от чего он зависит и как связан с коэфф. Пуассона

ξ= v/(l-v), где ξ — коэффициент бокового давления грунта., v-коэффициент бокового расширения грунта (коэффициент Пуассона). В общем случае коэффициент бокового давления грунтов | есть отношение приращения горизонтального давления грунта dqк приращению действующего вертикального давления dp, т. е. ξ = dq/ dp Отделяя переменные и интегрируя, получим q = ξ p + D. (2.13) Выражение (2.13) есть уравнение прямой с угловым коэффициентом ξ и постоянной интегрирования D, определяемой из начальных условий. Значения коэффициента бокового давления ξ получены следующие: для песчаных грунтов ξ = 0,25 — 0,37 и для глинистых (в зависимости от консистенции) ξ = 0,11-0,82.

71.Какова принципиальная схема стабилометра? Каким образом ведутся

Источник