Закон изменения напряжения в идеальном колебательном контуре

11 класс

§ 32. Процессы при гармонических колебаниях в колебательном контуре

Гармонические колебания заряда, силы тока и напряжения.

Подобно тому как координата при механических колебаниях меняется по гармоническому закону, точно так же заряд конденсатора меняется по закону синуса или косинуса:

q = q_msin (ωt + φ₀) или q = q_m cos (ωt + φ₀), (1)

где q_m — амплитуда колебаний заряда; φ₀ — начальная фаза колебаний.

Эти величины определяются начальными условиями, т. е. значениями заряда и силы тока в начальный момент времени: q(0) = q₀ и i(0) = i₀.

Если в начальный момент времени q(0) = q₀, а i(0) = 0, то колебания совершаются по косинусоидальному закону с нулевой начальной фазой φ₀ = 0 и амплитудой q_m = q₀:

Точно так же изменяется координата груза на пружине, если вывести груз из положения равновесия и не сообщать ему начальной скорости. Сила тока в контуре i = q’ (q’ — производная заряда по времени) также совершает гармонические колебания.

где I_m = ωq_m — амплитуда колебаний силы тока.

Сопоставив уравнения (1) и (2), можно сделать вывод, что колебания силы тока опережают колебания заряда по фазе на π/2 (рис. 6.5).

Напряжение на обкладках конденсатора также изменяется по гармоническому закону:

где U_m = q_m / C — амплитуда колебаний напряжения на обкладках конденсатора.

Превращение энергии в колебательном контуре.

Как изменяются энергии электрического и магнитного полей в идеальном колебательном контуре? Для ответа на этот вопрос воспользуемся рисунком 6.6.

Поскольку потерь энергии в рассматриваемом контуре нет, энергия всей колебательной системы (контура) постоянно перераспределяется между конденсатором и катушкой.

Рассмотрим момент, когда заряд конденсатора максимален и равен q_m, а ток отсутствует. В данном случае энергия магнитного поля катушки в этот момент времени равна нулю. Вся энергия W контура сосредоточена в конденсаторе:

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен I_m, а конденсатор полностью разряжен. Энергия электрического поля конденсатора в этот момент времени равна нулю. Вся энергия W контура запасена в катушке:

При отсутствии потерь на нагревание вещества и излучение электромагнитных волн максимальное значение энергии электрического поля конденсатора контура равно максимальному значению энергии магнитного поля катушки:

где U_m — максимальное значение напряжения на конденсаторе; I_m — максимальное значение силы тока в катушке. Согласно закону сохранения энергии, сумма мгновенных значений энергий электрического и магнитного полей в колебательном контуре в любой момент времени остаётся неизменной:

где u — мгновенное значение напряжения на конденсаторе; i — мгновенное значение силы тока в катушке.

Итак, в идеальном колебательном контуре в отдельные моменты времени энергия всей колебательной системы может сосредоточиться либо только в катушке индуктивности, либо только в конденсаторе. В действительности из-за энергетических потерь колебания будут затухающими. При достаточно большом сопротивлении колебания не возникают. Конденсатор разрядится, но его перезарядки при этом не произойдёт.

Вопросы:

1. По какому закону изменяются сила тока, напряжение и заряд при свободных электромагнитных колебаниях в контуре?

2. Как можно определить амплитуду колебаний:

б) напряжения на обкладках конденсатора?

3. Чему равна разность фаз между колебаниями силы тока и заряда в идеальном колебательном контуре?

4. В какие моменты времени энергия всей колебательной системы равна максимальному значению:

а) энергии электрического поля;

б) энергии магнитного поля?

Вопросы для обсуждения:

Нa рисунке 6.7 показаны процессы, происходящие в идеальном колебательном контуре за один период, а на рисунке 6.8 — графики, выражающие зависимости мгновенных значений силы тока и напряжения от времени.

а) Какому моменту времени соответствуют процессы в колебательном контуре, представленные на рисунке 6.7, в? Чему равна сила тока в катушке?

б) Какому моменту времени соответствуют процессы в колебательном контуре, изображённые на рисунке 6.7, д? Чему равно напряжение на обкладках конденсатора?

в) Какие преобразования энергии происходят в рассматриваемом контуре?

Пример решения задачи

Сила тока в идеальном колебательном контуре изменяется по гармоническому закону i(t) = 0,02sin 500πt (А). Индуктивность контура равна 0,1 Гн. Определите период колебаний, ёмкость конденсатора, максимальную энергию электрического поля.

Эта энергия по закону сохранения энергии равна энергии колебательного контура W и максимальной энергии W_э электрического ноля:

W_м = W_э .

Определим период колебаний в контуре:

Для определения ёмкости конденсатора воспользуемся формулой Томсона:

Подставляя числовые данные, получим:

Ответ: W_м = W_э = 2 • 10 -5 Дж; T = 4 • 10 -3 с; C = 4 мкФ.

Упражнения:

1. Чему равны амплитуда колебаний, период и циклическая частота, если заряд конденсатора колебательного контура изменяется с течением времени по закону:

а) q(t) = 3,5 ∙ 10 -5 cos 4πt (Кл);

б) q(t) = 5 ∙ 10 -6 cos 100πt (Кл);

в) q(t) = 0,4 ∙ 10 -3 sin 8πt (Кл)?

2. Заряд на обкладках конденсатора изменяется с течением времени по закону q(t) = 4 • 10 -6 cos 4πt (Кл). Чему равна фаза колебаний заряда спустя 5 с после начала колебаний?

3. В колебательном контуре заряд на пластинах конденсатора с ёмкостью 1 мкФ изменяется с течением времени по закону q(t) = 10 -6 Cos 10 4 πt (Кл). Определите индуктивность контура. Запишите уравнения зависимости силы тока и напряжения от времени. Найдите период и частоту колебаний, амплитуды заряда, силы тока и напряжения.

4. Чему равны амплитуда и период гармонических колебаний, графики которых показаны на рисунке 6.9? Запишите уравнения зависимости q = q(t), i = i(t).

5. По графикам зависимости силы тока в колебательном контуре от времени (рис. 6.10) найдите период колебаний. Запишите уравнения зависимости силы тока и заряда от времени.

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Колебательный контур

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

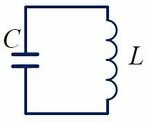
• Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения \(U_=\dfrac>\) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u \(\left(u = \dfrac \right).\) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e \(\left(W_=\dfrac><2c>=\dfrac> <2>\right),\) а сила тока в катушке i — энергию магнитного поля Wm \(\left(W_=\dfrac> <2>\right),\) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Источник

Колебательный контур принцип работы

Колебательный контур — принцип действия

Колебательный контур — это устройство, предназначенное для генерации (создания) электромагнитных колебаний.

Из чего он состоит?

Колебательный контур состоит из катушки и конденсатора. В нём может присутствовать резистор (элемент с переменным сопротивлением).

Катушка индуктивности (или соленоид) — это стержень, на который наматываются несколько слоёв обмотки медной проволокой. Этот элемент создаёт колебания в колебательном контуре. Стержень, находящийся в середине, называют дросселем, или сердечником.

Катушка колебательного контура создаёт колебания только при наличии запасённого заряда. При прохождении через неё тока она накапливает заряд, который затем отдаёт в цепь, если напряжение падает.

Провода катушки обычно имеют очень маленькое сопротивление, которое всегда остаётся постоянным. В цепи колебательного контура очень часто происходит изменение напряжения и силы тока. Это изменение подчиняется определённым математическим законам:

• U = U0*cos(w*(t-t0) , где U — напряжение в данный момент времени t, U0 — напряжение во время t0, w — частота электромагнитных колебаний.

Другим неотъемлемым компонентом контура является электрический конденсатор. Это элемент, состоящий из двух обкладок, которые разделены между собой диэлектриком. При этом толщина слоя между обкладками меньше их размеров. Такая конструкция позволяет накапливать на диэлектрике электрический заряд, который потом можно отдать в цепь.

Отличие конденсатора от аккумулятора в том, что в нём не происходит превращения веществ под действием электрического тока, а происходит непосредственное накопление заряда в электрическом поле. Таким образом, с помощью конденсатора можно накопить достаточно большой заряд, отдавать который можно весь сразу. При этом сила тока в цепи сильно возрастает.

Также колебательный контур состоит из ещё одного элемента: резистора. Этот элемент обладает сопротивлением и предназначен для контролирования силы тока и напряжения в цепи. Если при постоянном напряжении увеличивать сопротивление резистора, то сила тока будет уменьшаться по закону Ома:

• I = U/R , где I — сила тока, U — напряжение, R — сопротивление.

Катушка индуктивности

Давайте подробнее рассмотрим все тонкости работы катушки индуктивности и лучше поймём её функцию в колебательном контуре. Как мы уже говорили, сопротивление этого элемента стремится к нулю. Таким образом, при подключении к цепи постоянного тока произошло бы короткое замыкание. Однако если подключать катушку в цепь переменного тока, она работает исправно. Это позволяет сделать вывод о том, что элемент оказывает сопротивление переменному току.

Но почему это происходит и как возникает сопротивление при переменном токе? Для ответа на этот вопрос нам нужно обратиться к такому явлению, как самоиндукция. При прохождении тока по катушке в ней возникает электродвижущая сила (ЭДС), которая создаёт препятствие изменению тока. Величина этой силы зависит от двух факторов: индуктивности катушки и производной силы тока по времени. Математически эта зависимость выражается через уравнение:

• E = -L*I'(t) , где E — значение ЭДС, L — величина индуктивности катушки (для каждой катушки она разная и зависит от количества мотков обмотки и их толщины), I'(t) — производная силы тока по времени (скорость изменения силы тока).

Сила постоянного тока со временем не изменяется, поэтому сопротивления при его воздействии не возникает.

Но при переменном токе все его параметры постоянно изменяются по синусоидальному или косинусоидальному закону, вследствие чего возникает ЭДС, препятствующая этим изменениям. Такое сопротивление называют индукционным и вычисляют по формуле:

• XL = w*L, где w — частота колебаний контура, L — индуктивность катушки.

Сила тока в соленоиде линейно нарастает и убывает по различным законам. Это значит, что если прекратить подачу тока в катушку, она будет продолжать некоторое время отдавать заряд в цепь. А если при этом резко прервать подачу тока, то будет происходить удар из-за того, что заряд будет пытаться распределиться и выйти из катушки. Это — серьёзная проблема в промышленном производстве. Такой эффект (хотя и не совсем связанный с колебательным контуром) можно наблюдать, например, при вытаскивании вилки из розетки. При этом проскакивает искра, которая в таких масштабах не в силах нанести вред человеку. Она обусловлена тем, что магнитное поле не исчезает сразу, а постепенно рассеивается, индуцируя токи в других проводниках. В промышленных масштабах сила тока во много раз больше привычных нам 220 вольт, поэтому при прерывании цепи на производстве могут возникнуть искры такой силы, что причинят немало вреда как заводу, так и человеку.

Катушка — это основа того, из чего колебательный контур состоит. Индуктивности последовательно включённых соленоидов складываются. Далее мы подробнее рассмотрим все тонкости строения этого элемента.

Что такое индуктивность?

Индуктивность катушки колебательного контура — это индивидуальный показатель, численно равный электродвижущей силе (в вольтах), которая возникает в цепи при изменении силы тока на 1 А за 1 секунду. Если соленоид подключён к цепи постоянного тока, то её индуктивность описывает энергию магнитного поля, которое создаётся этим током по формуле:

• W=(L*I2)/2, где W — энергия магнитного поля.

Коэффициент индуктивности зависит от многих факторов: от геометрии соленоида, от магнитных характеристик сердечника и от количества мотков проволоки. Ещё одно свойство этого показателя в том, что он всегда положителен, потому что переменные, от которых она зависит, не могут быть отрицательными.

Индуктивность также можно определить как свойство проводника с током накапливать энергию в магнитном поле. Она измеряется в Генри (названа в честь американского учёного Джозефа Генри).

Кроме соленоида колебательный контур состоит из конденсатора, о котором пойдёт речь далее.

Электрический конденсатор

Ёмкость колебательного контура определяется ёмкостью электрического конденсатора. О его внешнем виде было написано выше. Теперь разберём физику процессов, которые протекают в нём.

Так как обкладки конденсатора сделаны из проводника, то по ним может течь электрический ток. Однако между двумя пластинами есть препятствие: диэлектрик (им может быть воздух, дерево или другой материал с высоким сопротивлением. Благодаря тому что заряд не может перейти от одного конца провода к другому, происходит накопление его на обкладках конденсатора. Тем самым возрастает мощность магнитного и электрического полей вокруг него. Таким образом, при прекращении поступления заряда вся электроэнергия, скопившаяся на обкладках, начинает передаваться в цепь.

Каждый конденсатор имеет номинальное напряжение, оптимальное для его работы. Если долго эксплуатировать этот элемент при напряжении выше номинального, срок его службы значительно сокращается. Конденсатор колебательного контура постоянно подвержен влиянию токов, и поэтому при его выборе следует быть предельно внимательным.

Кроме обычных конденсаторов, о которых шла речь, есть также ионисторы. Это более сложный элемент: его можно описать как нечто среднее между аккумулятором и конденсатором. Как правило, диэлектриком в ионисторе служат органические вещества, между которыми находится электролит. Вместе они создают двойной электрический слой, который и позволяет накапливать в этой конструкции в разы больше энергии, чем в традиционном конденсаторе.

Что такое ёмкость конденсатора?

Ёмкость конденсатора представляет собой отношение заряда конденсатора к напряжению, под которым он находится. Посчитать эту величину можно очень просто с помощью математической формулы:

• C = (e0*S)/d, гдеe0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.

Зависимость ёмкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между пластинами, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладок и меньше напряжение. А при уменьшении напряжения увеличивается значение ёмкости, так как её также можно описать следующей формулой:

• C = q/U, гдеq — заряд в кулонах.

Стоит поговорить о единицах измерения этой величины. Ёмкость измеряется в фарадах. 1 фарад — достаточно большая величина, поэтому существующие конденсаторы (но не ионисторы) имеют ёмкость, измеряемую в пикофарадах (одна триллионная фарада).

Резистор

Ток в колебательном контуре зависит также от сопротивления цепи. И кроме описанных двух элементов, из которых состоит колебательный контур (катушки, конденсатора), имеется ещё и третий — резистор. Он отвечает за создание сопротивления. Резистор отличается от других элементов тем, что имеет большое сопротивление, которое в некоторых моделях можно изменять. В колебательном контуре он выполняет функцию регулятора мощности магнитного поля. Можно соединить несколько резисторов последовательно или параллельно, тем самым увеличив сопротивление цепи.

Сопротивление этого элемента зависит также от температуры, поэтому следует быть внимательным к его работе в цепи, так как при прохождении тока он нагревается.

Сопротивление резистора измеряется в Омах, а его значение можно вычислить по формуле:

• R = (p*l)/S, где p — удельное сопротивление материала резистора (измеряется в (Ом*мм2)/м); l — длина резистора (в метрах); S — площадь сечения (в квадратных миллиметрах).

Как связать параметры контура?

Теперь мы вплотную подошли к физике работы колебательного контура. Со временем заряд на обкладках конденсатора изменяется согласно дифференциальному уравнению второго порядка.

Если решить это уравнение, из него следует несколько интересных формул, описывающих процессы, протекающие в контуре. Например, циклическую частоту можно выразить через ёмкость и индуктивность.

Однако наиболее простая формула, которая позволяет вычислить многие неизвестные величины, — формула Томсона (названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году):

• T = 2*п*(L*C)1/2.T — период электромагнитных колебаний, L и C — соответственно, индуктивность катушки колебательного контура и ёмкость элементов контура, п — число пи.

Добротность

Ещё одна важная величина, характеризующая работу контура, — добротность. Понять, что это, поможет такое явление как резонанс. Объяснить резонанс можно на простом примере: если вы начнёте подталкивать качели в такт их частоте, то они будут ускоряться, а их «амплитуда» будет возрастать. А если будете толкать не в такт, то они будут замедляться. При резонансе очень часто рассеивается много энергии. Для того, чтобы вычислить величины потерь, придумали такой параметр, как добротность. Она представляет собой коэффициент, равный отношению энергии, находящейся в системе, к потерям, происходящим в цепи за один цикл.

Добротность контура вычисляется по формуле:

• Q = (w0*W)/P, где w0 — резонансная циклическая частота колебаний; W — энергия, запасённая в колебательной системе; P — рассеиваемая мощность.

Этот параметр — безразмерная величина, так как фактически показывает отношение энергий: запасённой к потраченной.

Что такое идеальный колебательный контур

Для лучшего понимания процессов в этой системе физики придумали так называемый идеальный колебательный контур. Это математическая модель, представляющая цепь как систему с нулевым сопротивлением. В ней возникают незатухающие гармонические колебания. Такая модель позволяет получить формулы приближённого вычисления параметров контура.

Один из таких параметров — полная энергия:

Такие упрощения существенно ускоряют расчёты и позволяют оценить характеристики цепи с заданными показателями.

Как это работает?

Весь цикл работы колебательного контура можно разделить на две части.

• Первая фаза: пластина конденсатора, заряженная положительно, начинает разряжаться, отдавая ток в цепь. В этот момент ток идёт от положительного заряда к отрицательному, проходя при этом через катушку. Вследствие этого в контуре возникают электромагнитные колебания. Ток, пройдя через катушку, переходит на вторую пластину и заряжает её положительно (тогда как первая обкладка, с которой шёл ток, заряжается отрицательно).
• Вторая фаза: происходит прямо обратный процесс. Ток переходит с положительной пластины (которая в самом начале была отрицательной) на отрицательную, проходя опять через катушку. И все заряды встают на свои места.

Цикл повторяется до тех пор, пока на конденсаторе будет заряд. В идеальном колебательном контуре этот процесс происходит бесконечно, а в реальном неизбежны потери энергии из-за различных факторов: нагрева, который происходит из-за существования сопротивления в цепи (джоулевое тепло), и тому подобное.

Варианты конструкции контура

Кроме простых цепей «катушка-конденсатор» и «катушка-резистор-конденсатор», существуют и другие варианты, использующие в качестве основы колебательный контур. Это, например, параллельный контур, который отличается тем, что существует как элемент электрической цепи (потому как, существуй он отдельно, то являлся бы последовательной цепью, о которой и шла речь в статье).

Также существуют и другие виды конструкции, включающие разные электротехнические компоненты. Например, можно подключать в сеть транзистор, который будет размыкать и замыкать цепь с частотой, равной частотой колебаний в контуре. Таким образом, в системе установятся незатухающие колебания.

Где применяется колебательный контур?

Самое знакомое нам применение составляющих контура — это электромагниты. Они, в свою очередь, используются в домофонах, электродвигателях, датчиках и во многих других не столь обыденных областях. Другое применение — генератор колебаний. На самом деле это использование контура нам очень знакомо: в этом виде он применяется в микроволновке для создания волн и в мобильной и радиосвязи для передачи информации на расстояние. Всё это происходит благодаря тому, что колебания электромагнитных волн можно закодировать таким образом, что станет возможным передавать информацию на большие расстояния.

Катушка индуктивности сама по себе может использоваться как элемент трасформатора: две катушки с разным числом обмоток могут передавать с помощью электромагнитного поля свой заряд. Но так как характеристики соленоидов различаются, то и показатели тока в двух цепях, к которым подключены эти две индуктивности, будут различаться. Таким образом можно преобразовывать ток с напряжением в 220 вольт в ток с напряжением в 12 вольт.

Источник