Скорость движения электронов
Уже упоминалось, что электроны движутся в направлении анода ускоренно, и это без всяких преувеличений соответствует действительности. В тот момент, когда электрон покидает область катода, его скорость теоретически принимается равной нулю, однако, он, находясь в постоянном электрическом поле анода, начинает двигаться ускоренно, и приобретает энергию, пропорциональную ускоряющему напряжению:
е — заряд электрона, принимается равным ≈ 1,602 х 10 -19 Кл;
те — масса электрона, принимается равной ≈ 9,11 х 10 -31 кг;
Решая это уравнение относительно скорости электрона υ, получим следующее выражение:
В науке часто используется отношение заряда электрона к его массе, е/те, которое имеет приближенное значение 1,7588 х 10 11 Кл/кг. При приложении к аноду относительно катода напряжения 100 В электрон достигнет поверхности анода, имея скорость порядка 6 х 10 б м/с.
Если использовать предыдущее выражение и подставить в него ускоряющее напряжение 512 кВ, (величина, соответствующая, например, напряжению в дальних линиях электропередач), то получится, что скорость электрона может превысить скорость света, что, естественно, является невозможным. Причина заключается в том, что приведенное упрощенное выражение справедливо только для массы покоя электрона, однако, при движении с околосветовыми скоростями масса электрона возрастает, требуя бесконечно большого значения напряжения для ускорения электрона до околосветовых скоростей. С учетом этих условий необходимо использовать более сложное уравнение, предложенное Элли (Alley) и Этвудом (Atwood):
в котором с — скорость света в вакууме, примерно равна 2,998 х 10 8 м/с.
В качестве домашнего примера действие принципа относительности можно продемонстрировать на цветном телевизоре. Для исправного цветного кинескопа напряжение на втором аноде составляет порядка 25 кВ, поэтому скорость электрона в момент удара о поверхность кинескопа составляет более 300 млн км/час, однако более простое уравнение предсказывает скорость, на 3,5% более высокую.
В рентгеновских медицинских установках мишень бомбардируется электронами, имеющими очень высокую скорость, так как для возникновения рентгеновского излучения скорость электрона при соударении должна значительно превышать 300 млн км в час. Поэтому в кинескопах домашних телевизоров и мониторов (для снижения интенсивности рентгеновского излучения) не используется ускоряющее напряжение, превышающее 25 кВ, хотя при этом можно было бы обеспечить более высокую четкость и фокусировку изображения.
Необходимо учесть, что расстояние между анодом и катодом не входит в каждое из уравнений, хотя теоретически бесконечное расстояние позволило бы бесконечно возрасти времени, во время которого происходит ускорение движения, и даже при сравнительно небольших ускорениях скорость при ударе могла бы оказаться значительной.
Очень многие явления, происходящие внутри электронных ламп, могут быть поняты при понимании процессов, происходящих при ускоренном движении электрона в электрическом поле анода, приобретении им кинетической энергии и процессах передачи энергии электрона при ударе, когда он достигает анода.
Все сказанное выше вполне справедливо для обсуждения скорости движения ускоренных положительным полем электронов, подлетающих к аноду. Однако в области катода картина совсем иная. Дело в том, что кинетическая энергия электронов, преодолевших работу выхода из металла и покинувших катод, оказывается различной. Таким образом, отрываясь от катода, электроны начинают движение к аноду с различными начальными скоростями. Они невелики, но при детальном рассмотрении их нельзя считать одинаковыми, как это предполагалось выше, когда рассматривался ускоренный поток электронов, подлетающих к аноду. Как будет показано ниже, управление электронным потоком в триодах и более сложных электронных лампах осуществляется как раз вблизи катода. Из физической статистики известно, что из-за различных кинетических энергий, скорости электронов, вылетающих из катода распределены по так называемому закону распределения Максвелла. Однако, для дальнейших рассуждений наиболее важным фактом является тот факт, что электроны, вылетающие из катода, обладают различными кинетическими энергиями.
Источник
Лекция 4
1.2.5. Зависимость скорости электрона от напряженности электрического поля. Понятия эффективной массы и подвижности.
электрический ток в образце зависит не только от концентрации носителей заряда, но и от скорости с которой они переносятся под действием электрического поля. После того как мы научились рассчитывать концентрацию свободных носителей в твердом теле рассмотрим как ведут себя носители заряда в кристалле при наложении на него электрического поля.
Рассмотрение начнем с поведения единичного свободного заряда в нейтральной не взаимодействующей с зарядом среде (допустим в вакууме) при наличии электрического поля E, которое накладывается на среду в моментt=0. Электрическое поле приводит к возникновению силы электростатического взаимодействияF, под действием которой электрон начнет ускоряться.
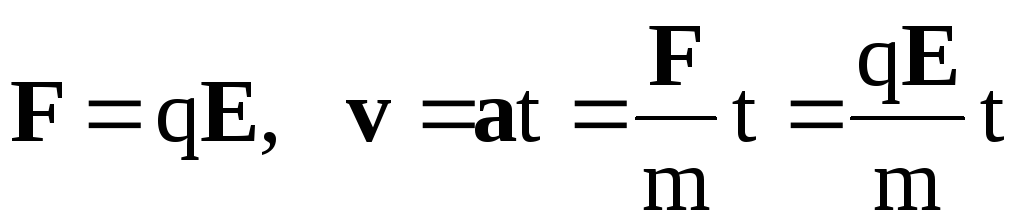
где q,m– заряд и масса электрона,vиaего скорость и ускорение. Таким образом в электрическом поле заряженная частица разгоняется с постоянным ускорением пропорциональным напряженности электрического поля и обратно пропорциональным ее массе. При этом энергия частицы будет изменяться со временем по квадратичному закону относительно импульса частиц или ее волнового вектораk(p= ћk, где ћ =h/(2π), h – постоянная Планка).
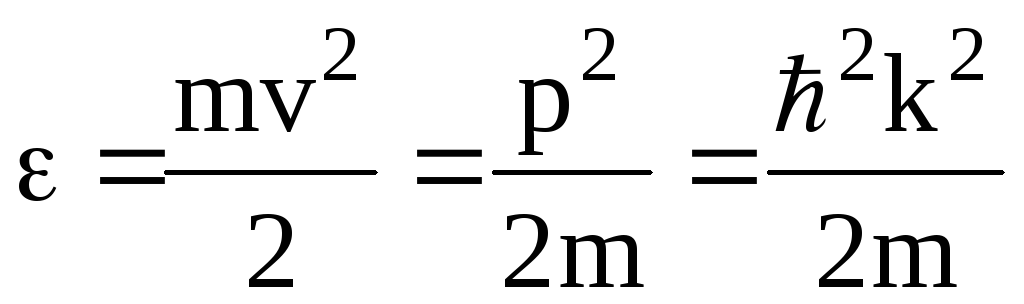
Поскольку приобретаемая заряженной частицей энергия не зависит от направления электрического поля зависимость (1.5) симметрична относительно импульса и волнового вектора (это параболоид выпуклость которого определяется массой частицы).
Измерив зависимость энергии частицы от импульса (или волнового числа мы можем ) используя (1.5) определить эффективную массу. Действительно дважды продифференцировав (1.5) получим.
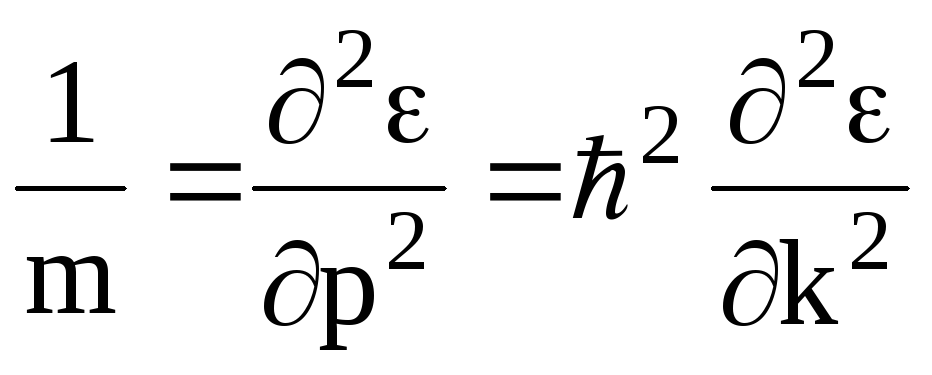
Предположим, что на частицу действует некоторая тормозящая сила F* о существовании которой мы не знаем. Тогда уравнение (1.4) можно переписать в следующем виде:
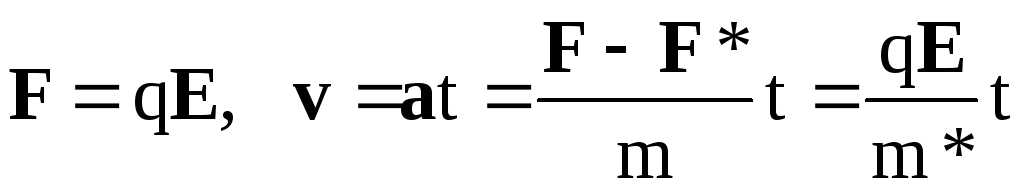
Соответственно, если для определения массы электрона (или любой другой заряженной частицы) в некоторой взаимодействующей с частицей среде воспользуемся формулой (1.6), то вместо массы электрона будет рассчитана некоторая другая величина, которую будем назвать эффективной массой электрона в данной среде.
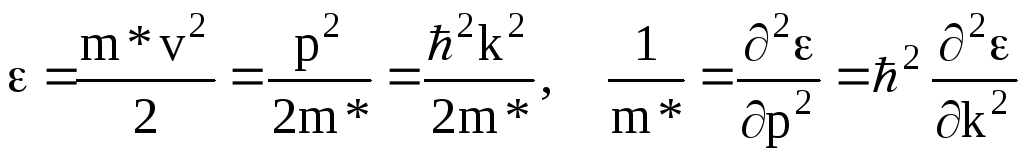
Поскольку при движении электронов (или других заряженных частиц) в твердом теле внутренние поля неизвестны, то их характеристики используют понятие эффективной массы.
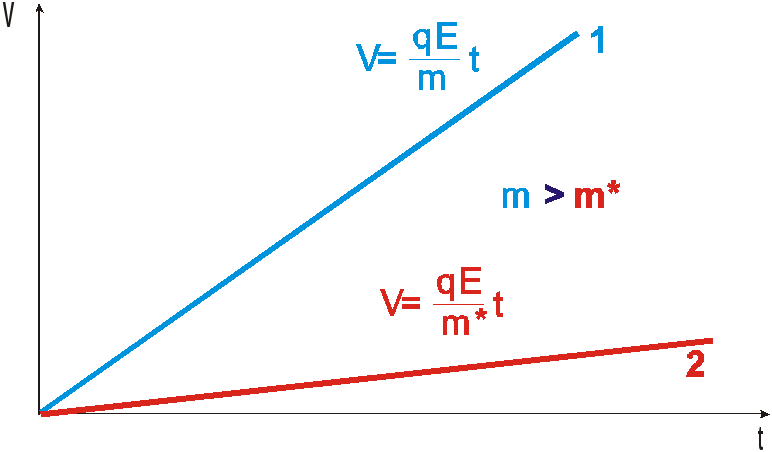
Рис. 1.18. Изменение скорости заряженной частицы в электрическом поле, при отсутствии взаимодействия со средой(1) и при торможении частицы средой.
На рис. 1.5 показано как будет со временем изменяться скорость свободной частицы в электрическом поле, в соответствии с (1.4) и (1.7 ). Эти формулы справедливы для случая, когда заряженная частица не испытывает столкновений и в соответствии с ними частицу можно разогнать электрическим полем до бесконечной энергии. Именно этот принцип был использован в первых линейных ускорителях элементарных частиц.
По мере разгона частицы возрастает ее импульс и соответствующее ему волновое число (величина, характеризующая величину волнового вектора). На рис. 1.6. показаны соответствующие зависимости изменения энергии частицы от величины волнового числа (импульса).
Рис. 1.19. Зависимости энергии свободных зарядов от величины их волнового числа (импульса).
Как видно из рис. 1.18. и рис. 1.19 набираемая в электрическом поле энергия частицы зависит от скорости частицы (волнового числа) и массы. Поскольку выпуклость кривой характеризуется ее второй производной можно сделать вывод, что чем меньше эффективная масса частицы, тем больше выпуклость, см. (1.27) и (1.29).
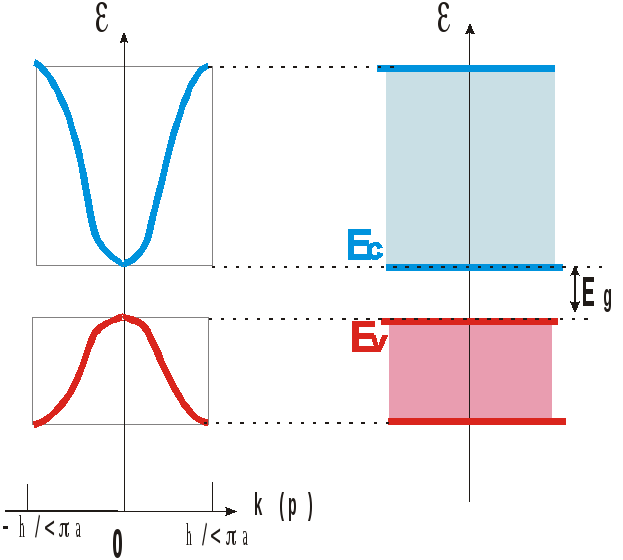
В кристалле энергия электрона (дырки) в разрешенной зоне не может превысить значение потолка разрешенной зоны, следовательно импульс и волновой вектор так же имеют ограничения, причем максимальное значение волнового числа должно быть кратно постоянной решетки. На рис. 1.20 показана рассчитанное изменение энергии электрона от величины волнового числа (значения) импульса для кубического кристалла.
Рис. 1.20. Зависимость энергии от волнового числа (импульса) в кристалле (a– постоянная решетки вдоль заданного направления)
Из рисунка видно, что в электронном представлении у потолка валентной зоны знак эффективной массы изменяется (должно происходить отражение частицы). Следует отметить, что у дна зоны проводимости энергия имеет параболическую зависимость от импульса (волнового числа):
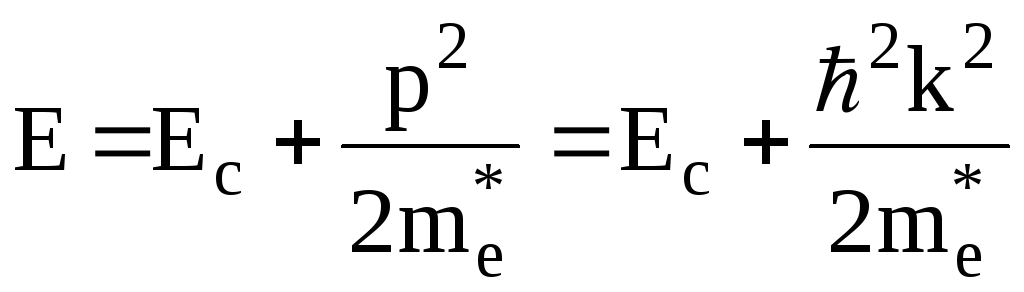
Если вести отсчет от дна зоны проводимости Ec= 0, то зависимость энергии электрона от импульса (волнового вектора) будет такая же как для свободного электрона см. (1.26). Это дает нам основание рассматривать электроны в зоне проводимости, находящиеся вблизи дна зоны проводимости как свободные частицы (иногда говорят квазисвободные или квазичастицы), считая что они подчиняются тем же закономерностям, что и свободные частицы, но отличаются от них величиной эффективной массы, которую вблизи дна зоны можно считать постоянной (пока выполняется параболическое приближение).
Аналогичный подход справедлив и для дырки. Вводя дырку мы переходим от электронного представления к дырочному, т.е. мы принимаем, то масса дырки положительная, а заряд отрицательный и энергия ее отсчитывается от потолка валентной зоны к ее дну, тогда дырка будет вести себя так же как электрон у потолка валентной зоны. При этом энергия дырки у потолка валентной зоны так же изменяется по параболическому закону как и для электрона:
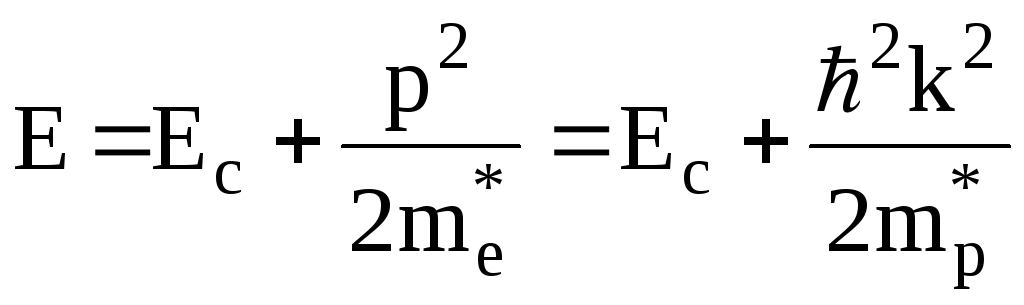
Таким образом дырку, находящуюся потолка валентной зоны так же можно рассматривать как свободную частицу.
В реальной жизни электрон в электрическом поле не может набирать энергию до бесконечности, рано или поздно он столкнется с другой частицей и отдаст ей накопленную энергию. Вероятность столкновений частиц в газах и твердых телах характеризуется временем или длиной их свободного пробега. Эти же величины характеризуют движение носителей заряда в твердом теле.
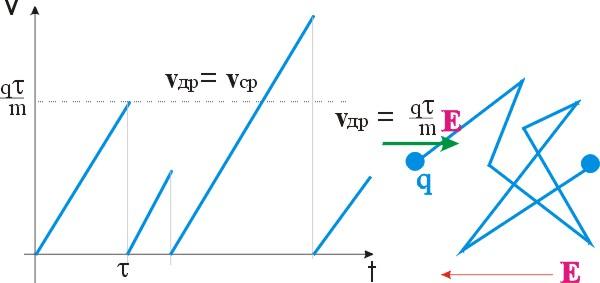
Схема, приведенная на рис. 1.21 показывает изменение скорости электрона в образце, к которому приложено напряжение и поясняет физический смысл подвижности. Электрон участвует в хаотическом тепловом движении, причем в различные моменты времени его скорость имеет случайное направление так что смещение его в любом направлении равновероятно. В электрическом поле электрон приобретает дополнительную скорость под действием поля, так что продолжая участвовать в тепловом движении он постепенно смещается под действием поля. Средняя скорость тем выше, чем больше длина свободного пробега и чем меньше эффективная масса частицы.
Рис. 1. 21. Диаграмма, поясняющая движение электрона в твердом теле
Поскольку электрон набирает энергию в поле за время свободного пробега и отдает ее при столкновении с решеткой или другими носителями заряда, то средняя скорость, которую приобретают носители в направлении поля, будем называть ее скоростью дрейфа зарядов vдрдолжна зависеть от средней длины свободного пробега τ.
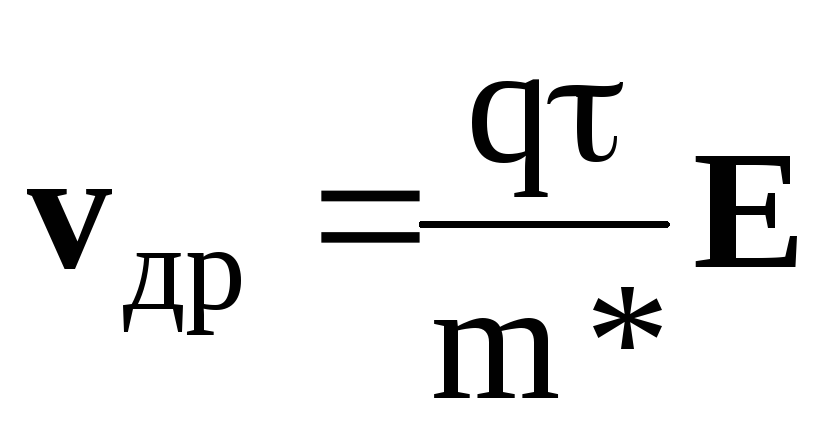
Коэффициент пропорциональности между дрейфовой скоростью и напряженностью электрического поля обычно называют подвижностью носителей заряда и обозначают μ:
Как видно из (1.36) и (1.37) подвижность имеет размерность в системе СИ м 2 /(Вс) , широко так же используются значения подвижности с размерностью см 2 /(Вс).
Предположим, что ток через ток образце создается электронами концентрация которых n см -3 и средняя дрейфовая скорость vдр. Поскольку величина тока равна заряду, проходящему через сечение образца в единицу времени можем записать:
Для единичной площади из (1.35) получится уравнение для плотности тока:
Поскольку в дифференциальной форме закон Ома имеет вид:
где σ – электропроводность образца (Ом . м или Ом . см )
Сравнив (1.39) и (1.40) получим формулу для электропроводности:
Если электрический ток создается различными носителями (всего Nтипов) с концентрацией каждого типаni , то:
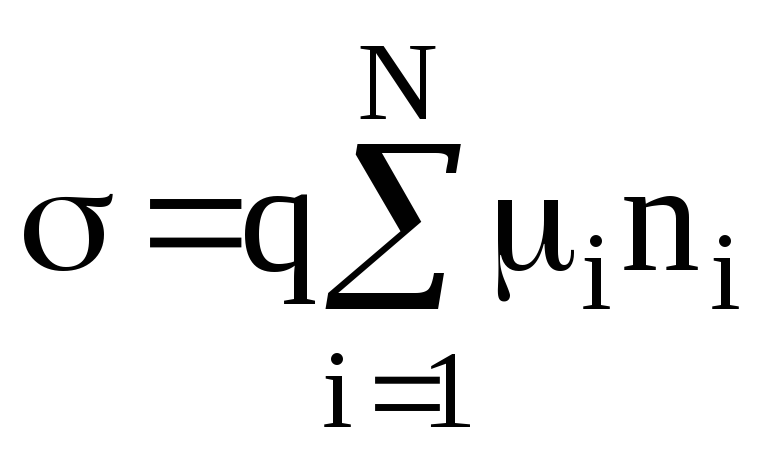
таким борзом мы видим, что проводимость материала определяется двумя основными параметрами: подвижностью носителей заряда и их концентрацией.
Величина подвижности пропорциональна длине свободного пробега, которая зависит от частоты столкновений носителей заряда с решеткой или атомами примеси. Поскольку при столкновениях носители отдают энергию, а затем вновь набирают, т.е. энергия носителя релаксирует, то принято говорить о механизмах ее релаксации. За время релаксации принимают среднее время в течение которого электрон полностью отдает свою энергию.
Существует множество механизмов рассеяния (релаксации ) энергии свободных носителей заряда. Однако, для полупроводников, наиболее существенные два: рассеяние на решетки и рассеяние на ионизованной примеси.
Для рассеяния на решетке справедливо :
T -3/2 и с ростом температуры подвижность носителей падает. Действительно длина свободного пробега носителей заряда тем меньше, чем сильнее колеблется решеткаl
1/T, для скорости носителей справедливоv
1/T 3/2 . Таким образом рост, в случае если доминирует рассеяние на решетке (примесей мало), то с ростом температуры подвижность падает и следовательно падает проводимость ( как это имеет место в металлах).
При рассеянии на заряженной примеси μi
Таким образом, если в образце доминирует рассеяние на примесях, то с ростом температуры подвижность возрастает и соответственно возрастает проводимость.
Значения множителей μr0 и μi0зависят от химического состава материала, наличия в нем дефектов и примесей, степени их ионизации (для разных образцов одного материала эти значения могут быть различными).
При одновременном действии нескольких механизмов рассеяния для расчета подвижности можно воспользоваться понятием эффективной подвижности носителей, которая будет определяться всеми, имеющими место механизмами рассеяния. Для случая, когда доминирует рассеяние на колебаниях решетки и ионизованной примеси для эффективной подвижности можно записать (считая, что акты рассеяния — независимые события):
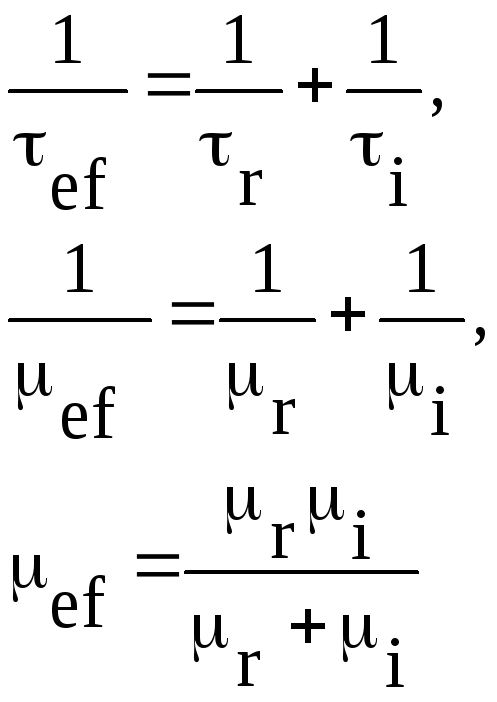
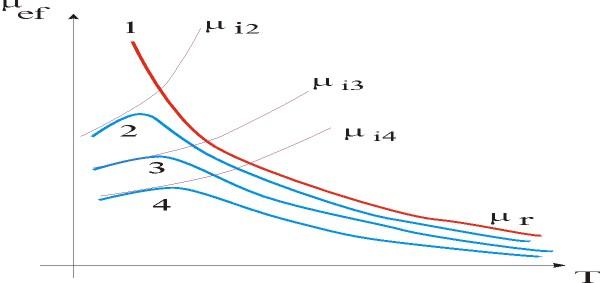
На рис. 1.21 схематически показана зависимость эффективной подвижности от температуры в полупроводниковом материале с разной концентрацией примеси. Графики построены в соответствии с формулами (1.43) и (1.45). Кривая 1 соответствует образцу без примесей. Кривые 2, 3, 4 образцам с разным содержанием примеси (большему номеру соответствует большее содержание примеси). На этом же график приведены соответствующие кривые для чисто решеточного μrи примесного рассеяния: μr2, μr3, μr4.
Характер изменения электропроводности полупроводников с температурой, в том случае, если не изменяется концентрация носителей заряда будет определяться температурной зависимостью подвижности и зависимости будут аналогичны показанным на рис. 2 (это может быть в примесной области температурной зависимости проводимости).
Рис. 1.21. Диаграмма, поясняющая температурную зависимость подвижности μef, при рассеянии на решетке μrи ионизированной примеси μiK.
Источник