- Катушка индуктивности: параметры и характеристики.
- Индуктивность в цепи постоянного тока
- Индуктивность в цепи переменного тока
- №20 Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности.
- Индуктивность катушки, её назначение, характеристики, формулы
- Общие сведения
- Способы расчёта
- Через силу тока
- Соленоид конечной длины
- Катушка с тороидальным сердечником
- Длинный проводник
- Варианты измерения
- Прямой метод
- Косвенное определение
Катушка индуктивности: параметры и характеристики.
Индуктивность в цепи постоянного тока
Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.

Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции.
Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону.
Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения.
Продолжительность нарастания тока в секундах определяется по формуле:
где L — индуктивность катушки в генри , а R — общее сопротивление всей цепи в омах .
Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна:
t=3•0,6/60=0,03 сек.
При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице «Электромагнетизм» рис.е).
В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.
Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания.
Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток.
Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.
Индуктивность в цепи переменного тока
Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков.
Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть.
Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.
Будет иначе, если в цепь катушки подать переменный ток.
При этом магнитное поле катушки индуктивности становится тоже переменным.
На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.
Рассмотрим график происходящих процессов в катушке индуктивности.
При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º ) на катушку поступает нарастающее напряжение и ее магнитное поле «расширяется», накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке.
За другую четверть периода ( 90º-180º ), когда напряжение на катушке индуктивности уменьшается, магнитное поле «сворачивается», индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже «помочь» уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору.
Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю.
Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление , как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе — наоборот.
Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления , не вызывает безвозвратных потерь энергии.
Допустим, возьмем идеальную катушку , в которой не учитываются сопротивления провода и другие потери.
Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL ,которое измеряется в омах и вычисляется по формуле:
где f — частота тока в герцах (Гц), а L — индуктивность катушки в генри (Г).
Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.
К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц.
XL=2π•50•5=1570 Ом.
На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц — 31МОм. На графике показана зависимость упомянутой катушки от частоты.
Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку:
Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц.
I= 0,4/2•3,14•5•10 3 •500•10 -6 =0,25 мА
В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот.
На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис. а ).
Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно: 
и называется импедансом.
На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз , которая шунтирует индуктивность (рис. b ).
Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость .
Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки.
Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь: 
Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200.
Чтобы достигнуть такого качества используют следующие средства:
— применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода);
— увеличение толщины провода, что, правда, увеличит габариты катушки;
— в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга.
Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки.
Одним из способов является перекрестная намотка типа «универсаль» (рис. c ). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис. d,e ).
Источник
№20 Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности.
Если в катушке, изображенной на рис. 20.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (20.1) она равна:
где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: ψ = Li.
Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).
Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:
На рис. 2.18 показано изображение индуктивности на электрической схеме; uL – напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами, напряжение, наведенное в катушке собственным переменным магнитным полем.
Рис. 2.18 — Обозначение индуктивности
Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:
Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:
ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.
Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.
Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:
В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:
Это – мгновенное значение напряжения. Его амплитуда равна:
Аналогичное выражение получается (после деления на √2) и для действующих значений:
где Bl — индуктивная проводимость.
Запишем соответствующие формулы в символической форме:
Аналогично для действующих значений
Уравнения, связывающие напряжение и ток в индуктивности, как в вещественных, так и в комплексных числах, представляют собой закон Ома для индуктивности.
Начальная фаза напряжения больше начальной фазы тока на 90° . В индуктивности ток отстает от напряжения на четверть периода. Выражение закона Ома, записанное в символическое форме, указывает на этот сдвиг фаз. Вспомним, что умножение вектора на j приводит к его повороту на угол 90° против часовой стрелки.
Рис. 2.19 — Векторная диаграмма напряжения и тока в индуктивности
Согласно уравнениям (2.18) UL получается путем умножения произведения IxL на j, в результате чего вектор UL оказывается повернутым относительно вектора I.
Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением uL = 200 sin(ωt+60°)В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.
Решение. При частоте f = 50 Гц циклическая частота ω = 314 с-1, и индуктивное сопротивление xL = ωL = 20 Ом. Амплитуда тока равна:
Так как в индуктивности ток отстает от напряжения на четверть периода, его начальная фаза меньше начальной фазы напряжения на 90° : ψi = ψu – 90° = 60–90–30°.
Итак, i = 10sin (ωt–30°). Векторная диаграмма показана на рис. 2.20.
Источник
Индуктивность катушки, её назначение, характеристики, формулы

Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
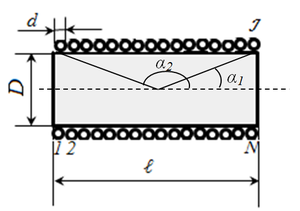
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Варианты измерения
Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.
Прямой метод
Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.
Порядок проведения измерений включает в себя следующие этапы:
- К прямопоказывающему приспособлению подключают катушку.
- После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
- Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.
Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.
Измерение выполняют путём проведения таких действий:
- Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
- Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
- После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
- Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
- На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
- После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
- Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.
Косвенное определение
Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).
Порядок определения параметра:
- К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
Аналогично подсоединяют и частотомер.
- Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
- Затем обе цепи подключают параллельно друг к другу.
- Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
- Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
- После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
- Как только эти действия будут выполнены, можно фиксировать значения.
Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.
После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:
- X — индуктивное сопротивление;
- π — математическая постоянная (примерно 3,14);
- F — частота в герцах, при которой проводились измерения.
Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.
Источник





















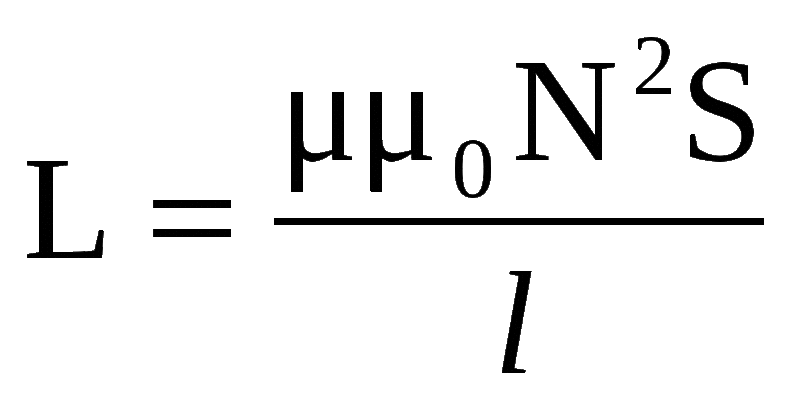
 µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
 l — длина проводника в метрах;
l — длина проводника в метрах;
 Аналогично подсоединяют и частотомер.
Аналогично подсоединяют и частотомер.