- Определение напряжений в грунтax оснований от дейcтвия внешних нагрузок
- 5.2. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ОСНОВАНИЯХ
- 5.2.1. Однородное основание (ч. 1)
- ТАБЛИЦА 5.1. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА РАССЕИВАНИЯ НАПРЯЖЕНИЙ K
- ТАБЛИЦА 5.2. ЗНАЧЕНИЯ σz/р ОТ ВЕРТИКАЛЬНОЙ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
- ТАБЛИЦА 5.3. ЗНАЧЕНИЯ σz/р ОТ ВЕРТИКАЛЬНОЙ ТРЕУГОЛЬНОЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
Определение напряжений в грунтax оснований от дейcтвия внешних нагрузок
Напряжения в массиве грунта, находящегося под действием внешней нагрузки, определяют с помощью решений теории упругости.
Для оценки несущей способности и деформирования оснований необходимо уметь определять напряжения, возникающие в различных точках массива грунта, от внешних нarрузок. В этой связи наиболее важными являются вертикальные напряжения, возникающие в основаниях.
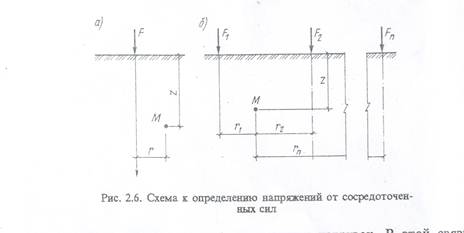
При действии вертикальной силы, приложенной к границе грунтового основания (рис. 2.6, а), вертикальные напряжения в точке М определяют из выражения
где k=(3/2)π[1+(r/z)²] 5/2 — безразмерный коэффициент, зависящий от соотношения r/z; F — вертикальная сила; z и r- соответственно вертикальная и горизонтальная координаты точки М.
При действии нескольких сосредоточенных сил (рис. 2.6, б) напряжения определяют на основе принципа независимости действия сил:
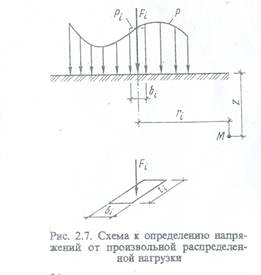
Если к поверхности основания приложена распределенная по некоторой площади внешняя нагрузка, закон изменения которой произволен (рис. 2.7), то напряжения в точке М определяют следующим образом. Загруженную площадъ разбивают на определенное количество элементарных участков квадратного или прямоугольного очертания, в пределах которых распределенную нагрузку заменяют сосредоточенной силой
Точность расчета, выполняемого с помощью данного метода, зависит от размеров элементарных участков и возрастает при увеличении их числа и удалении от точек приложения элементарных сил.
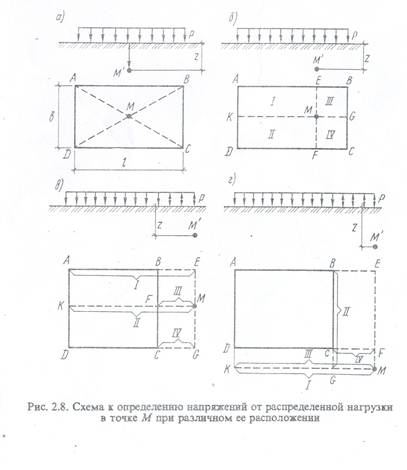
Напряжения, возникающие в грунтах в точках, находящихся на вертикали, проходящей под центром равномерной нагрузки, распределенной по прямо угольной площади (рис. 2.8, а), определяют из выражения
где а — коэффициент рассеивания напряжений, принимаемый в соответствии с данными табл. 2.1 в зависимости от соотношений ζ = 2z/ь и η= l/ ь (b и l — соответственно ширина и длина площади нагружения, z – вертикальная координата точки, где определяются напряжения); р — давление, приложенное к верхней плоскости основания.
Для площади загружения, представляющей собой правильный многогранник площадью А, значения а. можно определить, как для круглой площади загружения радиусом r=√A/b. При промежуточных значениях С и » коэффициент а. находят линейной интерполяцией.
| Значение α для фундаментов | |||||||||
| ζ=2z/b | круглых | Прямоугольных с отношением сторон η=l/b | Ленточных при η≥l0 | ||||||
| 1,4 | 1,8 | 2,4 | 3,2 | ||||||
| 0,0 | 1,009 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,4 | ‘0,949 | 0,960 | 0,972 | 0,975 | 0,976 | 0,976 | 0,977 | 0,977 | 0,977 |
| 0,8 | 0,756 | 0,800 | 0,848 | 0,966 | 0,870 | 0,876 | 0,879 | 0,881 | 0,881 |
| 1,2 | 0,547 | 0,606 | 0,682 | 0,717 | 0,727 | 0,740 | 0,749 | 0,754 | 0,755 |
| 1,6 | 0,390 | 0,449 | 0,532 | 0,578 | 0,593 | 0,612 | 0,630 | 0,639 | 0,642 |
| 2,0 | 0,285 | 0,336 | 0,414 | 0,463 | 0,481 | 0,505 | 0,529 | 0,545 | 0,550 |
| 2,4 | 0,214 | 0,257 | 0,325 | 0,374 | 0,392 | 0,419 | 0,449 | 0,470 | 0,477 |
| 2,8 | 0,165 | 0,201 | 0,260 | 0,304 | 0,321 | 0,350 | 0,383 | 0,410 | 0,42С |
| 3,2 | 0,130 | 0,160 | 0,210 | 0,251 | 0,267 | 0,294 | 0,329 | 0,360 | 0,374 |
| 3,6 | 0,106 | 0,130 | 0,173 | 0,209 | 0,224 | 0,250 | 0,285 | 0,320 | 0,337 |
| 4,0 | 0,087 | 0,108 | 0,145 | 0,176 | 0,190 | 0,214 | 0,248 | 0,285 | 0,306 |
| 4,4 | 0,073 | 0,091 | 0,122 | 0,150 | 0,163 | 0,185 | 0,218 | 0,256 | 0,280 |
| 4,8 | 0,062 | 0,077 | 0,105 | 0,130 | 0,141 | 0,161 | 0,192 | 0,230 | 0,258 |
| 5,2 | 0,053 | 0,066 | 0,091 | 0,112 | 0,123 | 0,141 | 0,170 | 0,203 | 0,239 |
| 5,6 | 0,046 | 0,058 | 0,079 | 0,099 | 0,108 | 0,124 | 0,152 | 0,189 | 0,223 |
| 6,0 | 0,040 | 0,051 | 0,070 | 0,087 | 0,095 | 0,110 | 0,136 | 0,172 | 0,208 |
| 6,8 | 0,032 | 0,040 | 0,055 | 0,069 | 0,076 | 0,088 | 0,110 | 0,144 | 0,184 |
| 7,6 | 0,024 | 0,032 | 0,044 | 0,056 | 0,062 | 0,072 | 0,091 | 0,123 | 0,166 |
| 8,4 | 0,021 | 0,026 | 0,037 | 0,046 | 0,051 | 0,060 | 0,077 | 0,105 | 0,150 |
| 9,2 | 0,018 | 0,022 | 0,031 | 0,039 | 0,043 | 0,051 | 0,065 | 0,091 | 0,137 |
| 0,015 | 0,019 | 0,026 | 0,033 | 0,037 | 0,044 | 0,056 | 0,079 | 0,126 | |
| 0,009 | 0,015 | 0,020 | 0,026 | 0,028 | 0,034 | 0,044 | 0,060 | 0,106 |
По данным табл. 2.1 можно определить напряжения и в точках, находящихся на вертикали, проходящей под угловыми точками прямоугольной площадки загружения (точка В на рис. 2.8, а), при этом ζ = z/ь. Напряжения под угловыми точками находят по формуле
Возможность находить напряжения в угловых точках позволяет определить напряжения в любой точке грунтового основания методом угловых точек. Если- точки, в которой требуется определить напряжение, находится в пределах площади загружений (точка М на рис. 2.8, 6), то площадь загружения разбивают на четыре прямоугольника: АЕМК. EBGM. КМFD и MGCF. для каждого прямоугольника точка М будет угловой, тогда, напряжение можно найти суммированием от четырех площадей зarружения I, II, III и IV:
Если же точка М находится вне пределов зarруженной площади ABCD (рис. 2.8, в), тогда ее считают угловой для четырех фиктивных площадей загружения: АЕМК. КМGD. BEMF и FMGC. При этом в пределах I и II зон зarружения направление нагрузки совпадает с направлением заданной, а в пределах III и IV зон принимается обратным исходному и напряжения определяют как

В случае расположения точки М’ вне пределов площади зarружения ABCD, как это показано на рис. 2.8, г, эту точку принимают за угловую для следующих фиктивных площадей загружения: АЕМК, BEMG, DFMK и CFMG. Напряжение находят из выражения
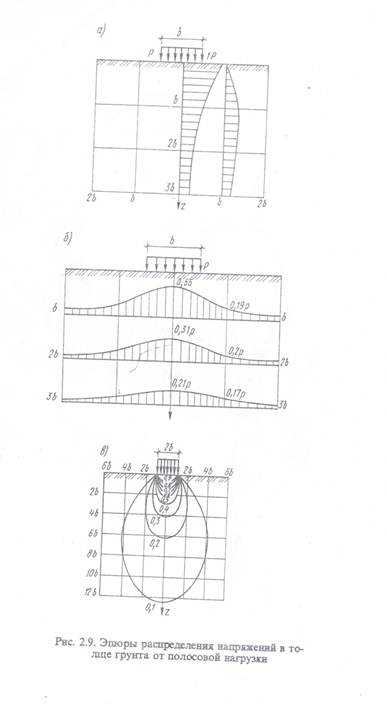
Изменение напряжений в толще основания обычно изображают с помощью эпюр. На рис. 2.9, а показано распределение вертикальных напряжений в массиве грунта от действия полосовой нагрузки, приложенной к границе основaния плоская задача теории упругости). Вертикальные напряжения убывают с глубиной, причем интенсивность уменьшения больше в — ближайшей зоне, примыкающей к границе загруженного основания. Распределение вертикальных напряжений по горизонтальным плоскостям показано на рис. 2.9, б, они убывают в горизонтальном направлении.
Часто об интенсивности напряженного состояния грунтов судят по линиям равных вертикальных напряжений (изобарам), показанных на рис. 2.9, в.
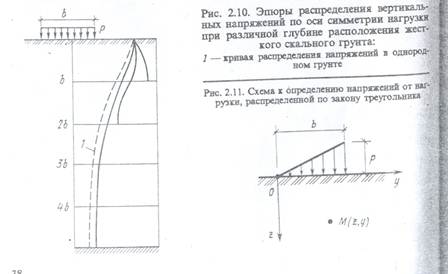
Приведенные выше формулы для определения напряжений справедливы не только для однородных оснований. Они могут быть использованы и для слоистых оснований при условии, что свойства отдельных пластов грунта незначительно отличаются друг от друга для слоистых оснований, свойства которых существенно различны, например основания, подстилаемого скальными грунтами, распределение напряжений будет иным из-за концентрации напряжений, которую необходимо учитывать в расчетах (рис. 2.10).
Для нагрузок, распределенных по поверхности основания по треугольному закону (рис. 2.11), вертикальные напряжения в толще основания определяют по формуле
где kz — коэффициент, зависящий от соотношений ζ = z/b и п= у/b;
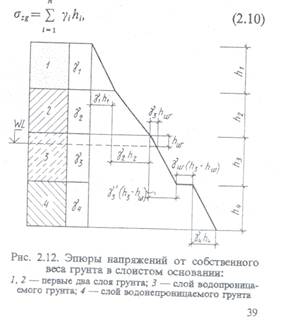
р — максимальное значение треугольной нагрузки. В основаниях кроме напряжений от внешней нагрузки, создаваемой фундаментами здaний и сооружедий, в каждой точке действуют вертикальные напряжения и от собственного веса вышележащих слоев, которые можно найти из выражения
где п — количество слоев грунта; γi — удельный вес грунта i-го слоя; ; hi — толща пласта i-го слоя грунта.
Из формулы (2.10) следует, что для однородного основания эпюра напряжений от собственного веса имеет вид треугольника для слоистого основания эпюра примет вид ломаной линии вследствие различных значений удельного веса отдельных пластов грунта (рис. 2.12).
В водопроницаемых грунтах, залегающих ниже отметки уровня подземных вод WL, при вычислении их удельного веса необходимо учитывать взвешивающее действие воды, определяемое согласно закону Архимеда.
В водонепроницаемых грунтах (глинах и СУГЛИВlCах в твердом или полутвердом состоянии), находящихся ниже уровня подземных вод, будет возвышать дополнительное гидростатическое давление от столба воды, расположенного над давным слоем.
При проектировании взаимодействие между основаниями и фундаментами и их влияние друг на друга учитывают с помощью контактных давлений, возникающих в грунтах по подошве фундамента.
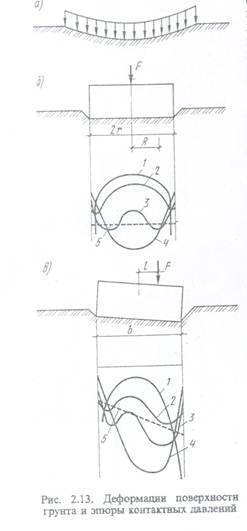
Выше были рассмотрены методы определения напряжений в массиве грунта от действия нагрузок, которые способны следовать за перемещениями грунта, формируя так называемую чашу оседания, поскольку напряжения под центром нагрузки больше, чем по краям (рис. 2.13, а).
Передача давления на грунт основания через подошву жесткого фундамента при центральноприложенной нагрузке вызовет равномерную осадку грунта. Равномерность осадки вызовет под подошвой фундамента неравномерное распределение давления. Имеется теоретическое решение задачи о распределении напряжений по подошве круглого абсолютно жесткого штампа:
где Ро — среднее давление по подошве штампа; R — расстояние ОТ оси симметрии; r — радиус подошвы фундамента.
Из этой формулы следует, что под центром штампа давление; будет иметь минимальное значение, а под краями – бесконечно большое (кривая 1 на рис. 2.13, 6), однако в реальных условиях грунты оснований не могут воспринимать бесконечно большие напряжения и их величина под краями штампа всегда имеет конечное значение (кривая 2).
При увеличении внешней нагрузки под краями штампа начинают развиваться зоны пластических деформаций, что вызывает перераспределение напряжений под подошвой с более нагруженных участков на менее нагруженные, и эпюра давлений приобретает седлообразное очертание (кривая 3). При дальнейшем возрастании нагрузки, приближающейся к предельному значению, эпюра давления становится колокообразной (кривая 4>. Очертание эпюры давления под подошвой фундамента зависит от внешней нагрузки развития зон пластических деформаций в грунте. В практических расчетах давление под подошвой фундамента условно усредняют и считают равномерно распределенным (линия 5).
Характер распределения давления по подошве внецентренно нагруженного фундамента в зависимости от внешней нагрузки показан на рис. 2.13, в. При проектировании внецентренно нагруженных фундаментов давление по подошве считается распределенным по закону трапеции (линия 5).
Осреднение давления по подошве фундамента и принятие допущения о его линейном распределении оправданы для расчета оснований и подбора размеров фундаментов, имеющих относительно высокую жесткость, поскольку в данном случае для основания контактные давления являются местной нагрузкой и существенным для него окажется не характер распределения, а величина и направление равнодействующей давления. Последние факторы и окажут решающее влияние на величину и характер деформации основания.
Для расчета и проектирования гибких фундаментов, имеющих сравнительно небольшую жесткость, следует учитывать очертание эпюры контактных давлений, так как в данном случае осреднение давления приведет к большим погрешностям в расчетах.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
5.2. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ОСНОВАНИЯХ
Напряжения в грунтах определяются с помощью теории линейно-деформируемой среды. При этом предполагается, что сжатие основания от собственного веса и внешней нагрузки закончилось, нагружение основания производится без разгрузки и внешнее давление на основание не превышает расчетного сопротивления.
Если из массива грунта, находящегося под действием какой-либо нагрузки, в том числе собственного веса грунта, выделить элементарный кубик со сторонами, параллельными выбранным осям прямоугольной системы координат, то в общем случае по граням его будут действовать составляющие напряжений σz , σx . σy — вертикальное и горизонтальные нормальные напряжения, параллельные соответственно осям z, х и y , и три пары касательных напряжений τzх и τxz , τху и τyx , τyz и τzy (рис. 5.2).
5.2.1. Однородное основание (ч. 1)
Для определения составляющих напряжений в однородном основании для наиболее часто встречающихся в практике проектирования случаев действия на поверхности основания вертикальной внешней нагрузки служат формулы и таблицы.
При сосредоточенной силе (рис. 5.3) составляющие напряжений имеют следующий вид:
В формуле для определения σz коэффициент K (табл. 5.1) вычисляется по зависимости
где 
ТАБЛИЦА 5.1. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА РАССЕИВАНИЯ НАПРЯЖЕНИЙ K
| r/z | K | r/z | K |
| 0,0 | 0,4775 | 1,8 | 0,0129 |
| 0,1 | 0,4657 | 1,9 | 0,0105 |
| 0,2 | 0,4329 | 2,0 | 0,0085 |
| 0,3 | 0,3849 | 2,1 | 0,0070 |
| 0,4 | 0,3295 | 2,2 | 0,0058 |
| 0,5 | 0,2733 | 2,3 | 0,0048 |
| 0,6 | 0,2214 | 2,4 | 0,0040 |
| 0,7 | 0,1762 | 2,5 | 0,0034 |
| 0,8 | 0,1386 | 2,6 | 0,0028 |
| 0,9 | 0,1083 | 2,7 | 0,0024 |
| 1,0 | 0,0844 | 2,8 | 0,0021 |
| 1,1 | 0,0658 | 2,9 | 0,0018 |
| 1,2 | 0,0513 | 3,0 | 0,0015 |
| 1,3 | 0,0403 | 3,5 | 0,0007 |
| 1,4 | 0,0317 | 4,0 | 0,0004 |
| 1,5 | 0,0251 | 4,5 | 0,0002 |
| 1,6 | 0,0200 | 5,0 | 0,0001 |
| 1,7 | 0,0160 |
При линейной нагрузке (рис. 5.4) составляющие напряжений определяются по формулам:
где 
При нагрузке, равномерно распределенной по полосе (рис. 5.5),
Значения σz/p приведены в табл. 5.2.
где
ТАБЛИЦА 5.2. ЗНАЧЕНИЯ σz/р ОТ ВЕРТИКАЛЬНОЙ НАГРУЗКИ, РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
| z/b1 | σz/р при x/b1 | |||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,5 | 0,7 | 1,0 | 1,5 | 2,0 | 3,0 | 4,0 | 5,0 | |
| 0,0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 0,500 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,1 | 1,000 | 1,000 | 0,999 | 0,999 | 0,998 | 0,993 | 0,500 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 |
| 0,2 | 0,997 | 0,997 | 0,996 | 0,995 | 0,988 | 0,959 | 0,500 | 0,011 | 0,002 | 0,000 | 0,000 | 0,000 |
| 0,3 | 0,990 | 0,989 | 0,987 | 0,984 | 0,967 | 0,908 | 0,499 | 0,031 | 0,005 | 0,001 | 0,000 | 0,000 |
| 0,5 | 0,959 | 0,958 | 0,953 | 0,943 | 0,902 | 0,808 | 0,497 | 0,089 | 0,019 | 0,003 | 0,001 | 0,000 |
| 0,7 | 0,910 | 0,908 | 0,899 | 0,885 | 0,831 | 0,732 | 0,492 | 0,148 | 0,042 | 0,007 | 0,002 | 0,001 |
| 1,0 | 0,818 | 0,815 | 0,805 | 0,789 | 0,735 | 0,650 | 0,480 | 0,214 | 0,084 | 0,017 | 0,005 | 0,002 |
| 1,5 | 0,668 | 0,666 | 0,658 | 0,646 | 0,607 | 0,552 | 0,448 | 0,271 | 0,146 | 0,042 | 0,015 | 0,006 |
| 2,0 | 0,550 | 0,548 | 0,543 | 0,535 | 0,510 | 0,475 | 0,409 | 0,288 | 0,185 | 0,071 | 0,029 | 0,013 |
| 3,0 | 0,396 | 0,395 | 0,393 | 0,390 | 0,379 | 0,364 | 0,334 | 0,274 | 0,211 | 0,114 | 0,059 | 0,032 |
| 4,0 | 0,306 | 0,305 | 0,304 | 0,303 | 0,298 | 0,290 | 0,275 | 0,242 | 0,205 | 0,134 | 0,083 | 0,051 |
| 5,0 | 0,248 | 0,248 | 0,247 | 0,246 | 0,244 | 0,239 | 0,231 | 0,212 | 0,188 | 0,139 | 0,097 | 0,065 |
При нагрузке, распределенной по полосе по закону треугольника (рис. 5.6), составляющие напряжений будут следующими:
Значения σz/р приведены в табл. 5.3.
ТАБЛИЦА 5.3. ЗНАЧЕНИЯ σz/р ОТ ВЕРТИКАЛЬНОЙ ТРЕУГОЛЬНОЙ НАГРУЗКИ, РАСПРЕДЕЛЕННОЙ ПО ПОЛОСЕ
| z/b1 | σz/р при x/b1 | ||||||||||
| –1,5 | –1,0 | –0,5 | 0,00 | 0,25 | 0,50 | 0,75 | 1,0 | 1,5 | 2,0 | 2,5 | |
| 0,00 | 0,000 | 0,000 | 0,000 | 0,000 | 0,250 | 0,500 | 0,750 | 0,500 | 0,000 | 0,000 | 0,000 |
| 0,25 | 0,000 | 0,001 | 0,004 | 0,075 | 0,257 | 0,480 | 0,645 | 0,422 | 0,015 | 0,002 | 0,000 |
| 0,50 | 0,002 | 0,005 | 0,022 | 0,127 | 0,262 | 0,409 | 0,473 | 0,352 | 0,062 | 0,012 | 0,003 |
| 0,75 | 0,005 | 0,014 | 0,045 | 0,153 | 0,247 | 0,334 | 0,360 | 0,295 | 0,101 | 0,028 | 0,010 |
| 1,0 | 0,011 | 0,025 | 0,064 | 0,159 | 0,223 | 0,275 | 0,287 | 0,250 | 0,121 | 0,046 | 0,018 |
| 1,5 | 0,023 | 0,045 | 0,085 | 0,147 | 0,177 | 0,198 | 0,202 | 0,187 | 0,126 | 0,069 | 0,036 |
| 2,0 | 0,035 | 0,057 | 0,089 | 0,127 | 0,143 | 0,153 | 0,155 | 0,148 | 0,115 | 0,078 | 0,048 |
| 3,0 | 0,046 | 0,062 | 0,080 | 0,095 | 0,101 | 0,104 | 0,105 | 0,102 | 0,091 | 0,074 | 0,057 |
| 4,0 | 0,048 | 0,058 | 0,067 | 0,075 | 0,077 | 0,079 | 0,079 | 0,078 | 0,073 | 0,064 | 0,054 |
| 5,0 | 0,045 | 0,051 | 0,057 | 0,061 | 0,063 | 0,063 | 0,063 | 0,063 | 0,060 | 0,055 | 0,049 |
| 6,0 | 0,041 | 0,046 | 0,049 | 0,052 | 0,052 | 0,053 | 0,053 | 0,053 | 0,051 | 0,048 | 0,044 |
Сорочан Е.А. Основания, фундаменты и подземные сооружения
Источник