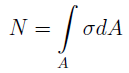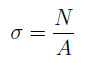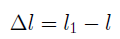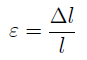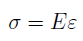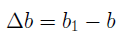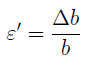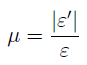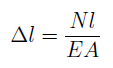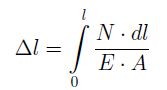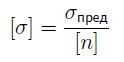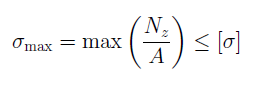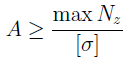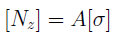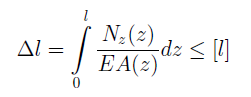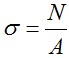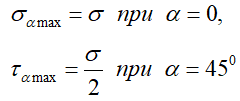В каких сечениях растянутого бруса возникают наибольшие нормальные напряжения

Растяжение-сжатие.

Внутренние усилия при растяжении-сжатии.

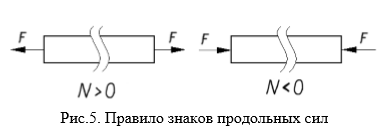
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)

Напряжения при растяжении-сжатии.

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
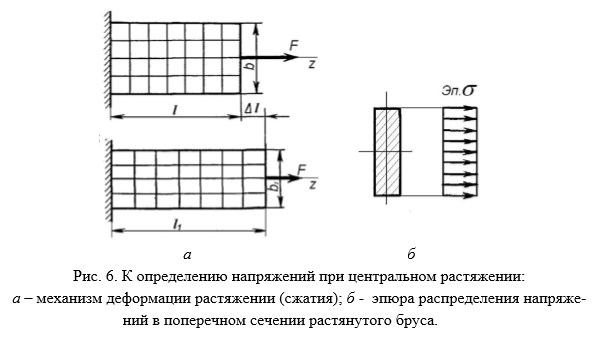
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.

Деформации при растяжении-сжатии.

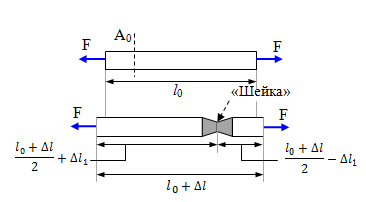
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l₁ и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

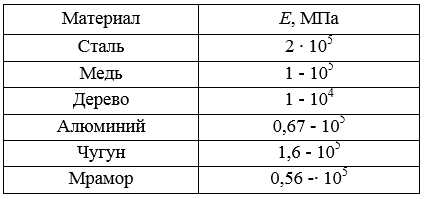
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε ‘ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε ‘ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

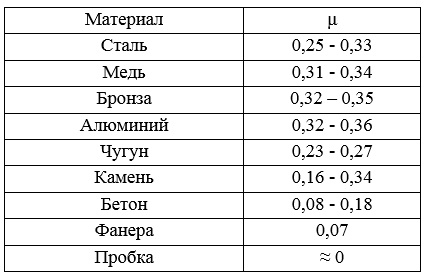
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно . В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).

Механические свойства материалов.

Основными механическими свойствами материалов при их деформации являются прочность , пластичность , хрупкость , упругость и твердость .

Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.

Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.

Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).

Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.

Твердость – свойство материала сопротивляться проникновению в него других тел.

Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l₀ и начальным постоянным поперечным сечением площади A₀ статически растягивается с обоих торцов силой F.

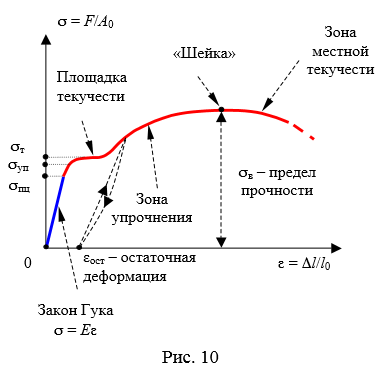
Диаграмма сжатия стержня имеет вид (рис. 10, а)

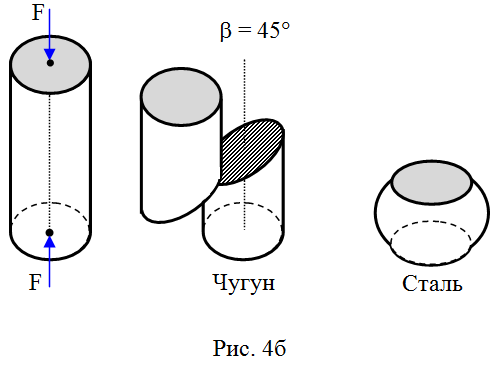
где Δl = l — l₀ абсолютное удлинение стержня; ε = Δl / l₀ — относительное продольное удлинение стержня; σ = F / A₀ — нормальное напряжение; E — модуль Юнга; σ_п — предел пропорциональности; σ_уп — предел упругости; σ_т — предел текучести; σ_в — предел прочности (временное сопротивление); ε_ост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ_0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σ_т глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.

Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σ_пред — предельное напряжение (σ_пред = σ_т — для пластических материалов и σ_пред = σ_в — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [n_т] = 1,2 … 2,5; для хрупких материалов [n] = [n_в] = 2 … 5, а для древесины [n] = 8 ÷ 12.

Расчеты на прочность при растяжении и сжатии.

Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.

Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.

Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.

Следующая важная статья теории:
Изгиб балки

Источник

iSopromat.ru

В поперечных сечениях при растяжении-сжатии имеют место только нормальные напряжения σ , которые определяются отношением внутренней силы N к площади A соответствующего поперечного сечения стержня.

Опытным путем показано, что при растяжении-сжатии, на достаточном удалении от точки приложения сил, вследствие равномерного распределения внутренних сил по сечению стержня в каждой его точке возникают напряжения одинаковой величины ( σ=const ).

Для обеспечения необходимой прочности элементов и конструкций напряжения не должны превышать допустимых значений.

Напряжения в наклонных сечениях

В наклонных сечения бруса одновременно с изменением величины нормальных напряжений появляются касательные.

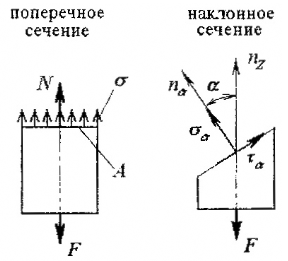
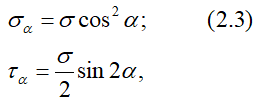
при этом

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

В каких сечениях растянутого бруса возникают наибольшие нормальные напряжения

— Что понимается под растяжением-сжатием?

— Какие случаи деформации бруса называются центральным растяжением или сжатием?

— С помощью какого метода определяют внутренние силы при растяжении брусьев?

— Как можно нагрузить прямой брус, чтобы он работал только на растяжение (сжатие)?

— Какие внутренние силовые факторы возникают в поперечном сечении стержня при его растяжении или сжатии?

— Как вычислить значение продольной силы в произвольном поперечном сечении бруса?

— Что представляет собой эпюра продольных сил и как она строится?

— Что такое продольная и поперечная деформация бруса при растяжении (сжатии) и какова зависимость между ними?

— Что называется полной (абсолютной) продольной деформацией? Что представляет собой относительная продольная деформация? Каковы размерности абсолютной и относительной продольной деформаций?

— По какой формуле определяется величина напряжения в поперечном сечении стержня?

— Какой вид нагружения (деформации) называют «центральным растяжением-сжатием»?

— Сформулируйте закон Гука для растяжения-сжатия? Приведите два выражения закона Гука и примеры их использования?

— Что называется модулем упругости Е ? Как влияет величина модуля Е на деформации бруса?

— Что называется модулем Юнга? В каких единицах он измеряется?

— Какие сечения стержня считаются опасными?

— Какое действие нагрузки называется статическим?

— Как определяется абсолютная продольная деформация?

— Что представляет собой эпюра продольных перемещений?

— Что называется жесткостью бруса при растяжении (сжатии)?

— Как формулируется закон Гука? Напишите формулы абсолютной и относительной продольной деформации бруса?

— Что происходит с поперечными размерами бруса при его растяжении и сжатии?

— Как определяется удлинение (укорочение) участка бруса с постоянным поперечным сечением и постоянной продольной силой по всей его длине?

— Как распределены нормальные напряжения σ _х в поперечных сечениях центрального растянутого бруса и чему они равны?

— В каких сечениях растянутого бруса возникают наибольшие нормальные напряжения?

— Как сопротивляются растяжению и сжатию пластичные и хрупкие материалы, одинаково или по-разному? Сопоставить диаграммы растяжения, сжатия для хрупких и пластичных материалов. Привести деформационные характеристики, определяющие степень пластичности материала?

— Нормативные и расчетные сопротивления материалов. Что принимается за нормативное сопротивление для пластичных и хрупких материалов?

— Методы расчета строительных конструкций?

— Как выполняются расчеты на прочность и жесткость при растяжении?

— Какие типы задач можно решить с учетом расчета на прочность?

— Что называется допускаемым напряжением? Как оно выбирается для пластичных и хрупких материалов?

— Что называется коэффициентом запаса прочности и от каких основных факторов зависит его величина?

— Какие три характерных типа задач встречаются при расчете прочности конструкции?

— Как выполняется проектировочный расчет?

— В чем смысл и какова формула поверочного расчета?

— Приведите известные методы расчетов на прочность?

— Что понимают под напряжением?

— Что называется однородным напряженным состоянием?

— Как распределены нормальные напряжения в поперечных сечениях центрально растянутого или сжатого бруса и чему они равны?

— Как вычисляются напряжения в любой точке наклонного сечения растянутого стержня?

— В каких сечениях растянутого стержня возникают наибольшие нормальные, а в каких – наибольшие касательные напряжения?

— Как используется гипотеза плоских сечений (гипотеза Бернулли) для выяснения закона распределения нормальных напряжений в поперечном сечении растянутого (сжатого) бруса?

— Как строится график (эпюра), показывающий изменение (по длине оси бруса) нормальных напряжений в поперечном сечении бруса?

— Каков физический смысл модуля продольной упругости?

— Что называется модулем упругости Е ? Как влияет величина модуля Е на деформации бруса?

— Что называется коэффициентом Пуассона?

— Какое напряжение называется допустимым и как его определяют для пластичных и хрупких материалов?

— Какие предельные напряжения приняты для различных групп материалов: хрупких, пластичных, хрупко-пластичных?

— Что такое требуемый коэффициент запаса прочности, и каковы принятые его числовые значения, исходя из свойств материалов?

— Что такое допускаемое напряжение и как оно выбирается в зависимости от механических свойств материалов?

— Почему считается возможным отклонение до 5% фактического напряжения от допустимого?

— Сформулируйте условие прочности, и как записывается в математической форме это условие при расчетах на растяжение — сжатие?

— Сколько различных видов расчета можно производить из условия прочности?

— Какие системы конструкции называются статически определимыми, и какие — статически неопределимыми?

— Каков общий порядок решения статически определимых задач?

— Назовите особенности расчета статически неопределимых систем?

— Какими свойствами обладают статически неопределимые конструкции?

— Что называется степенью статической неопределимости системы?

— Как определяется температурная деформация при растяжении-сжатии?

— Какие системы называются статически неопределимыми?

— Что представляют собой дополнительные уравнения условия совместности перемещений?

— Какие напряжения называются температурными?

— По каким формулам определяют напряжение и деформацию в стержне с учетом его собственного веса?

— Как влияет собственный вес бруса на его удлинение и на его прочность?

— Как учитывается собственный вес бруса в аналитическом выражении для продольной силы?

— Как объяснить наличие множителя 1/2 в формуле удлинения вертикального бруса постоянного сечения от собственного веса?

— В каких случаях могут возникнуть в брусьях (стержнях) температурные и монтажные напряжения?

— Что называется напряженным состоянием в точке тела?

— По каким формулам определяются нормальные и касательные напряжения, возникающие в наклонных площадках в случае плоского напряженного состояния?

— Какие используются гипотезы при выводе формулы определения нормальных напряжений в поперечных сечениях брусьев? Запишите формулу определения напряжений?

— Что представляет собой эпюра продольных сил и как она строится?

— Что называется продольной силой и как она определяется в произвольном поперечном сечении стержня?

— Какие три характерные задачи встречаются при расчете на прочность при растяжении – сжатии?

— Как связаны между собой напряжения в наклонных и поперечных сечениях растянутого стержня?

— Какими данными надо располагать, чтобы подсчитать максимальную грузоподъемность растянутого стержня?

— Что называется коэффициентом поперечной деформации (коэффициентом Пуассона) и какие он имеет значения?

— Как определяются продольные перемещения точек бруса при ступенчато ломаном сечении и продольных силах, постоянных в пределах отдельных участков?

— Как отражается увеличение жесткости отдельных элементов статически неопределимых систем на усилиях в этих и других элементах?

— При проведении расчета на прочность по предельным состояниям с чем сравнивают фактические напряжения?

Онлайн-калькулятор «Расчет прочности при растяжении-сжатии»

Источник